On the Variability
of Individual Judgment
Frederic Lyman Wells
IN the article "Statistics of American Psychologists "[1] Professor Cattell calls attention to the fact that if one endeavors to arrange and rearrange in serial order a number of given objects, the positions successively given them will vary somewhat as they would vary if the arrangements had been made one each by different observers. If we undertook to rearrange ten times a series of grays in order of brightness, we should no more get the same order each time than we should get identical orders from ten different subjects. Nor would our own orders vary approximately the same amount from the average ; sometimes we should be better, sometimes worse, judges, just as among our ten subjects some would be more discriminative, some less. The judgments of the same individual at different times are theoretically quite comparable to those of different individuals regardless of the factor of time.
In this way there may be illustrated a continuum between the subjective and objective classes
( 512) of judgment. In the case of gays, weights, or lines we assume a certain standard which we term the objective order, and which we determine through photometry or some analogous method. Because we have such methods, we do not need to have recourse to individual judgments to determine objective values, and these individual judgments give us a part of the personal equation ; the individual's sensibility to light, weight, etc. On the other hand, we have such subjective judgment as preferences in sculpture, painting, or music. In the first class we may arrange individuals in precise order for accuracy of discrimination ; in the second, one may with equally good taste vary his preferences within a considerable range. So far as any distinction on a statistical basis is possible, we might consider as subjective those types in which the various judgments of the individual formed a species of their own, varying from each other considerably less than from an equal number of judgments made by different individuals ; and consider as objective those in which an individual would vary from his own independent judgments about as much as the variation of an equal number of judgments by different individuals. For example, if A and B arranged ten pieces of music in order of preference, the orders would centre about each individual's own standard; but if A, B, C, D, etc., arranged ten graduated weights, the orders would theoretically all centre about a
( 513) common standard, the objective order of heaviness. The two categories would almost certainly be continuous. We may first consider from this viewpoint types of this first. or highly subjective, class of judgments, and compare these subsequently with examples of a more objective type.
Experiments in Preference
An obvious and serious difficulty with all experiments involving repeated judgments of the same thing are the factors of recognition and memory. Especially is this true of judgments of subjective preference with which we are to be lucre concerned. If the subject remembers his previous judgments, he will in spite of himself order his successive ones accordingly. The only practicable ways of meeting this difficulty are to make the series to be arranged as long was possible, and, to allow as much time as possible to elapse between the successive arrangements. A certain homogeneity in the series is necessary, and this made the selection of suitable material no easy task. A series of fifty colored souvenir postal cards, to be graded in order of individual preference, was finally decided upon as the most practica1 approach to the problem[2] The cards were approved
( 514) by the writer from selections made from the sample books of the Rotograph Company. They are all views of natural scenery, with the works of man a subordinate feature. In a few cards these last are altogether absent. The fifty cards were arranged by the five subjects, A—E, five times each, one week elapsing between each individual's successive arrangements. Single arrangements were also made by five additional subjects, F—J, and these, combined with the first arrangements of A—E, give, for comparison, a series of ten arrangements by different subjects. Subjects A, B, and C are men of special psychological training, D and E are women of moderate psychological training. Of the five subjects making single arrangements, all are men of special, though widely differing, psychological training. From these experiments are gathered the data to be discussed below.
The uniform attitude of the subjects toward the experiment was one of lack of confidence in the judgments. The time required to make a single arrangement varied from 15 to 45 minutes, the women taking as a. rule longer than the men, and the time, of course, decreasing with the successive arrangements. So far as exact positions of the cards were concerned, the subjects who made repeated judgments reported complete oblivescence except now and then with regard to first or last positions. Of course a remembered judgment
( 515) was not necessarily repeated nor were repeated judgments necessarily remembered ; subject E placed the same card last in each arrangement, and at the close expressed surprise at finding that she had done so. One subject expressed absolute certainty that new cards were being successively introduced. There was naturally subjective effort to judge independently of previous arrangements. Certain features are to be noted in the results indicating that the memory difficulty was fairly satisfactorily met.
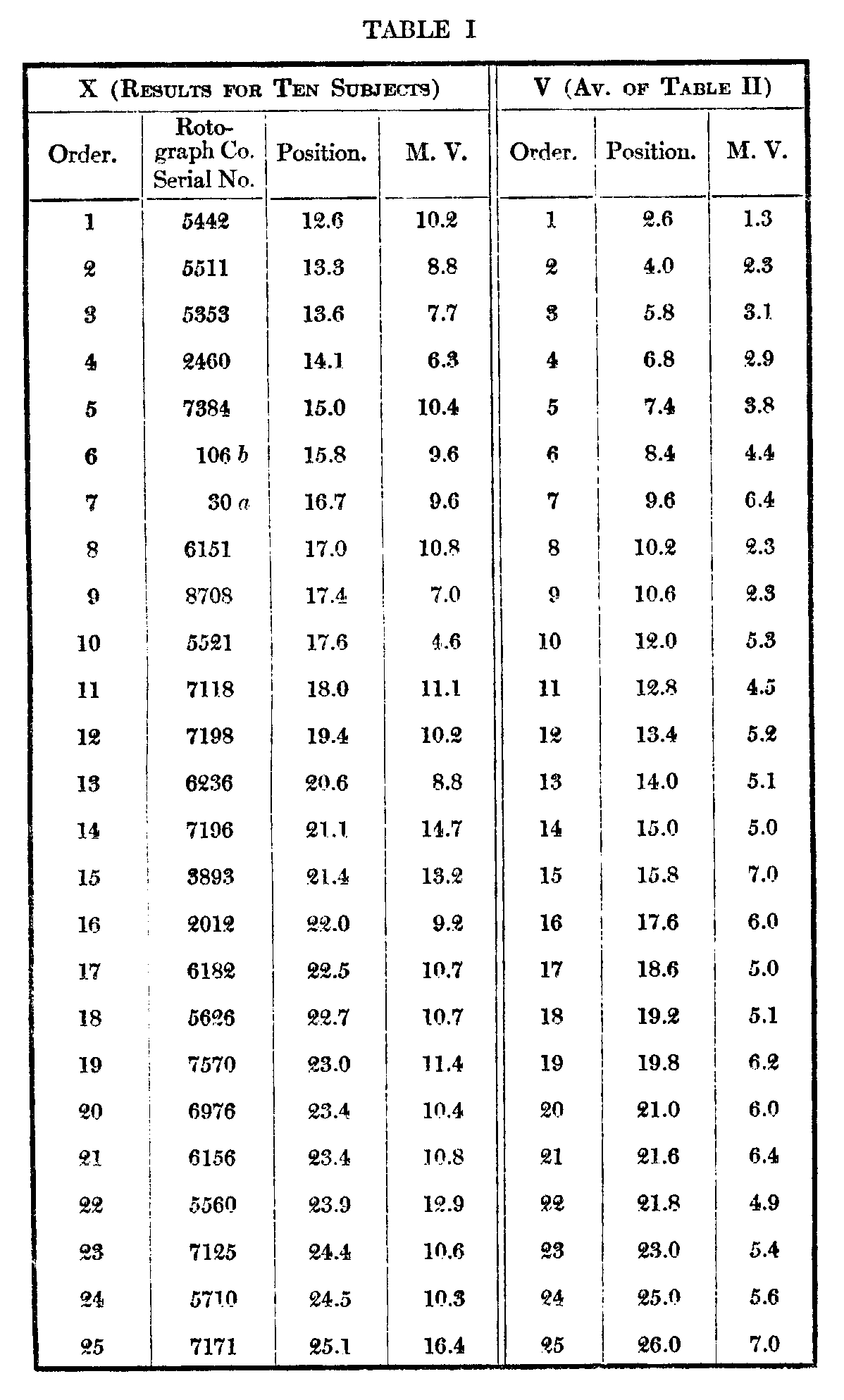
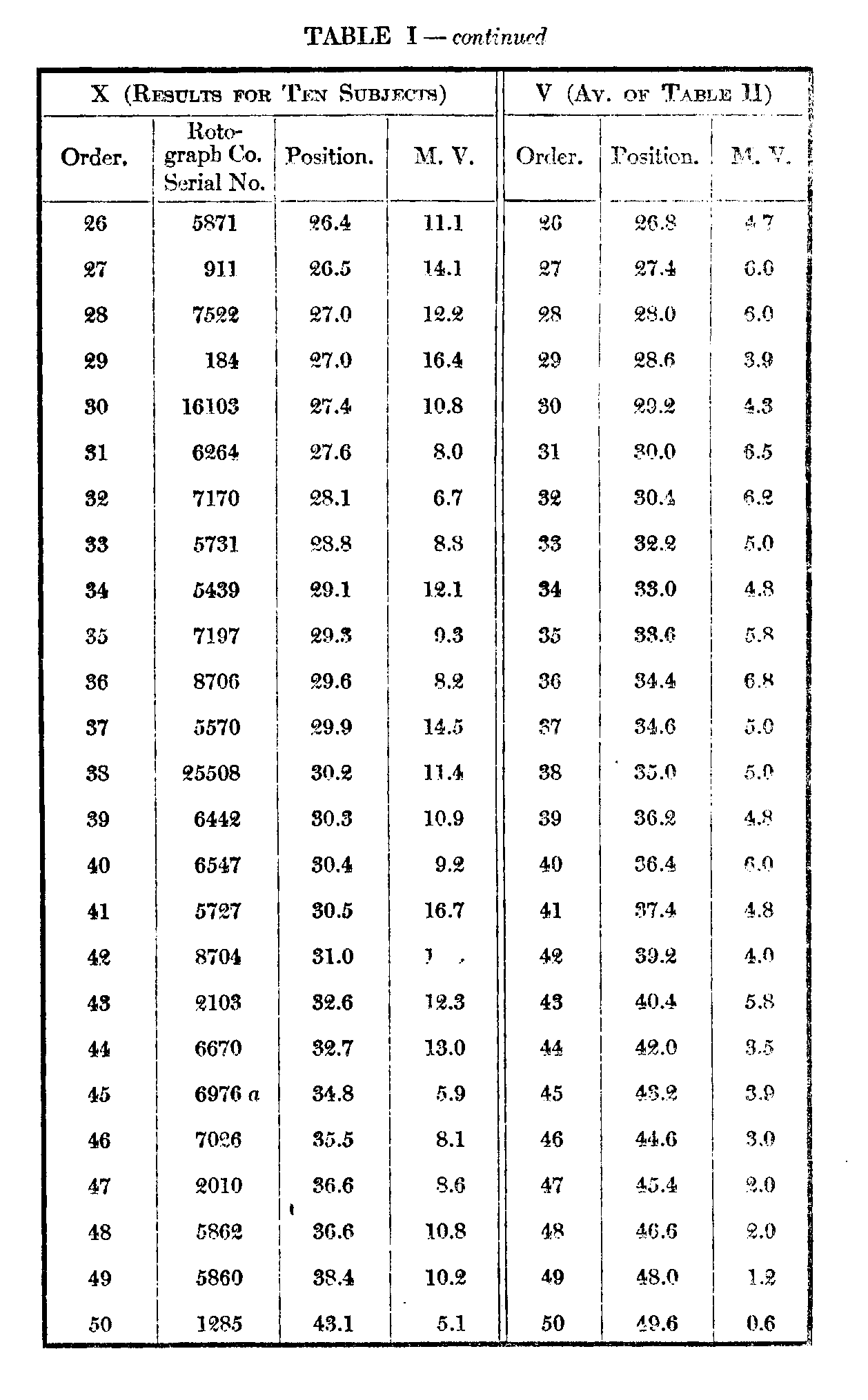
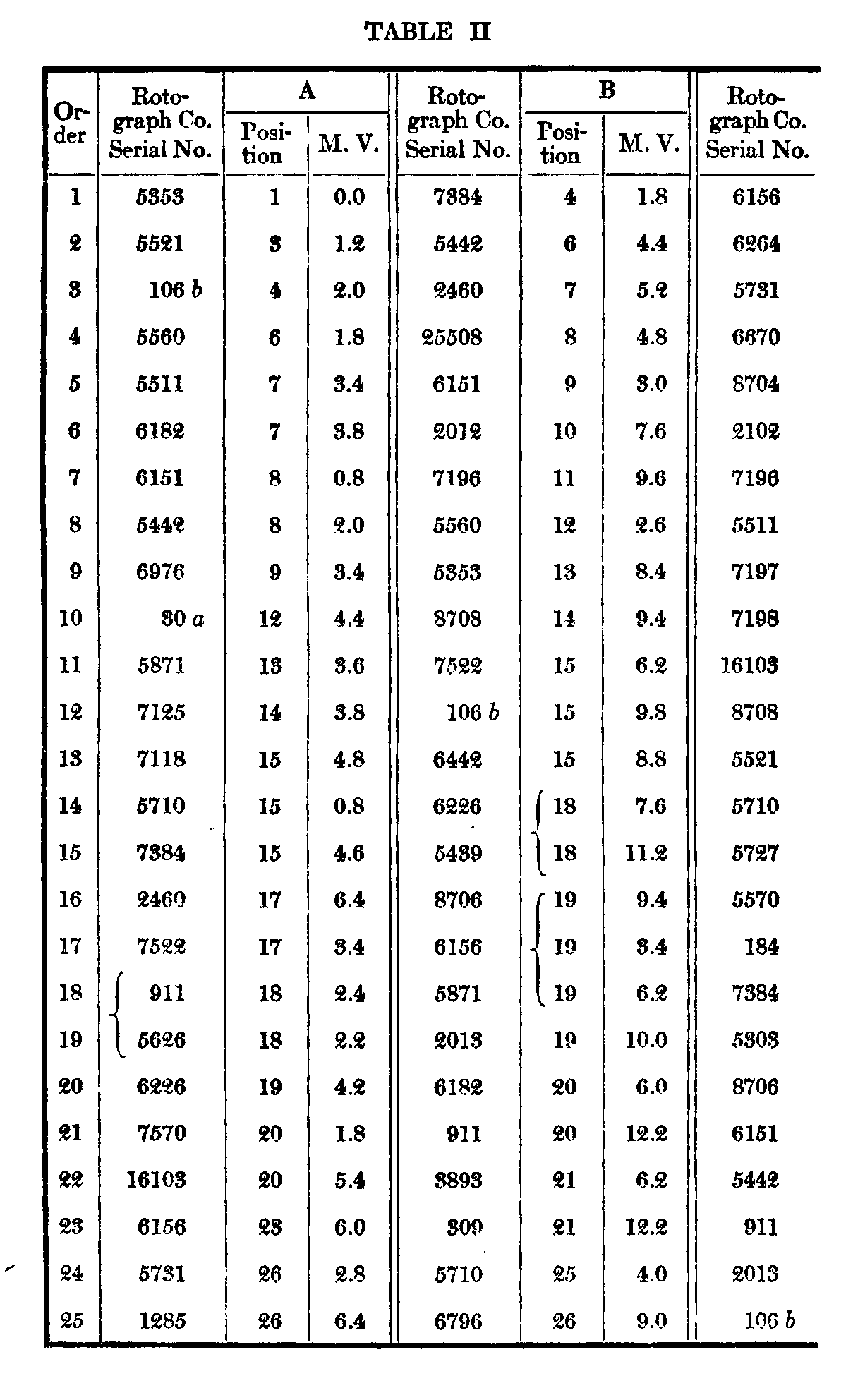
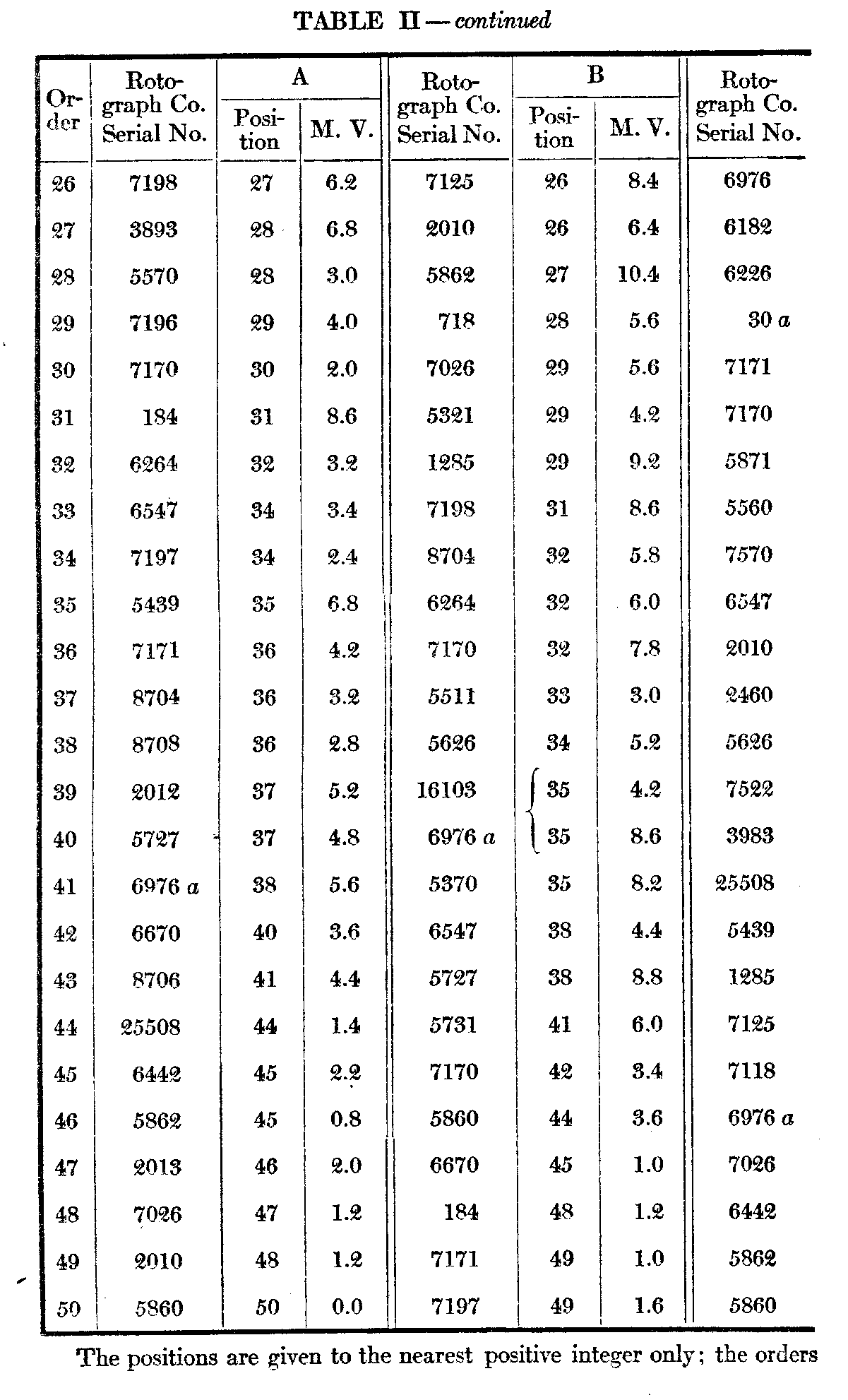
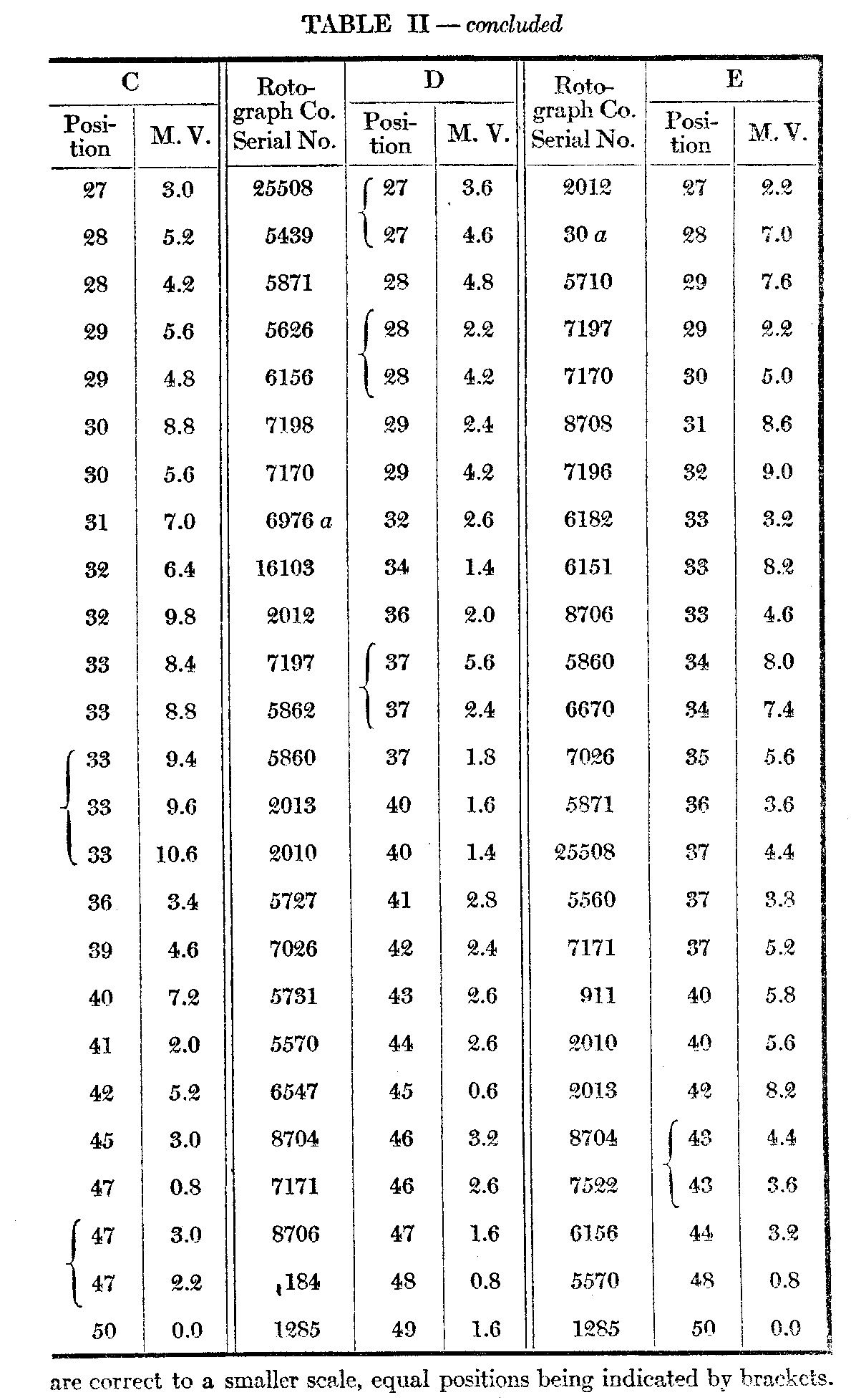
The subjoined Table I gives under X the order, average positions, and m. v. (not p. e.) of the single arrangements by the ten subjects. Column V is a combination of the records of subjects A--E which will be described below. Table II gives in detail the results of the five successive arrangements by each of the subjects A—E. To anyone interested in the statistics of such arrangements they will perhaps repay a more careful examination than it is possible to give them here.
When the subjects made the arrangements, it was customary to hesitate considerably on the first few and then to proceed at about an equal, or perhaps slightly increasing, rate to the end. This hardly reflects the size of the differences, which are presumably greatest at the ends. It is due merely to a natural tendency to exercise greater care at the beginning of the experiment. So far as the actual order is concerned they cannot have
( 516)
(517)
(518)
(519)

( 520)
( 521)
( 522) much bearing upon the experimental study of aesthetics, because the material would be too difficult to standardize for this purpose. Certain of the cards necessarily fall into groups through similarity of subject or color scheme, and these tend to keep rather together in position, also through the fact that they tend to become associated in memory. So far as establishing any objective basis for criteria of preferability is concerned, the results seem to me almost entirely negative.
It will perhaps be easier to consider in some detail the figures in Table I as a preliminary to the special results of the repeated arrangements in Table II. Column X presents almost a chaos of variability, the extreme range barely covering 30 places, with one exception only 26. The in. v.'s average nearly 11 places and range from the least variable card with an m. v. of 4.6 to the most variable with an m. v. of 16.7 over an approximately normal distribution as follows :
Variation 56789 10 11 12 13 14 15 16 17
No. cases 22157 8 13 3 3 2 1 2 1
Among the individual variations there are many above 25, the highest being 32. Card 2460, in which this variation occurs, has an average position of 33, and the individual places assigned to it by the ten subjects are respectively 42, 1, 40, 37, 43, 2, 42, 42, 41. A card graded first by one subject was in two cases graded last by another ; in a third, next to the last. One of the former is the
( 523) most variable card, 5727, and its grades are respectively 48, 44, 1, 43, 6, 48, 24, 33, 8, 50. The grades of the least variable card, 5521, are 2, 32, 17, 14, 20, 20, 15, 18, 20, 18; position 17.6. Anyone acquainted with the meaning of such figures as those given above must recognize the futility of attempting to evolve from them an order of any objective value.
This is much modified in the repeated arrangements by the same subject. It was noted above, that in objective judgments, as of weights, we should, theoretically, vary as much from our-selves as other people varied from each other, and from the comparison of these two variabilities might be deduced the degree of objectivity of the judgments. In the repeated arrangements it is at once evident that the range is much greater and the variability smaller. A table most comparable to X is given under V, which is computed as follows : Subject A's best card, as will be seen from Table II, receives an average of 1, B's an average of 4, C's 3, D's 3, and E's 2. Thus the average position of the best card of the five repeated judgments by five subjects is 2.6, and the average of the respective m. v.'s is 1.3, as opposed to 12.6 and 10.2 for individual judgments by ten subjects. The figures for last position are seen to be 49.6 and .6 as against 43.1 and 5.1. Of course the extreme positions might unduly favor the repeated judgments in this respect. But the figures for the
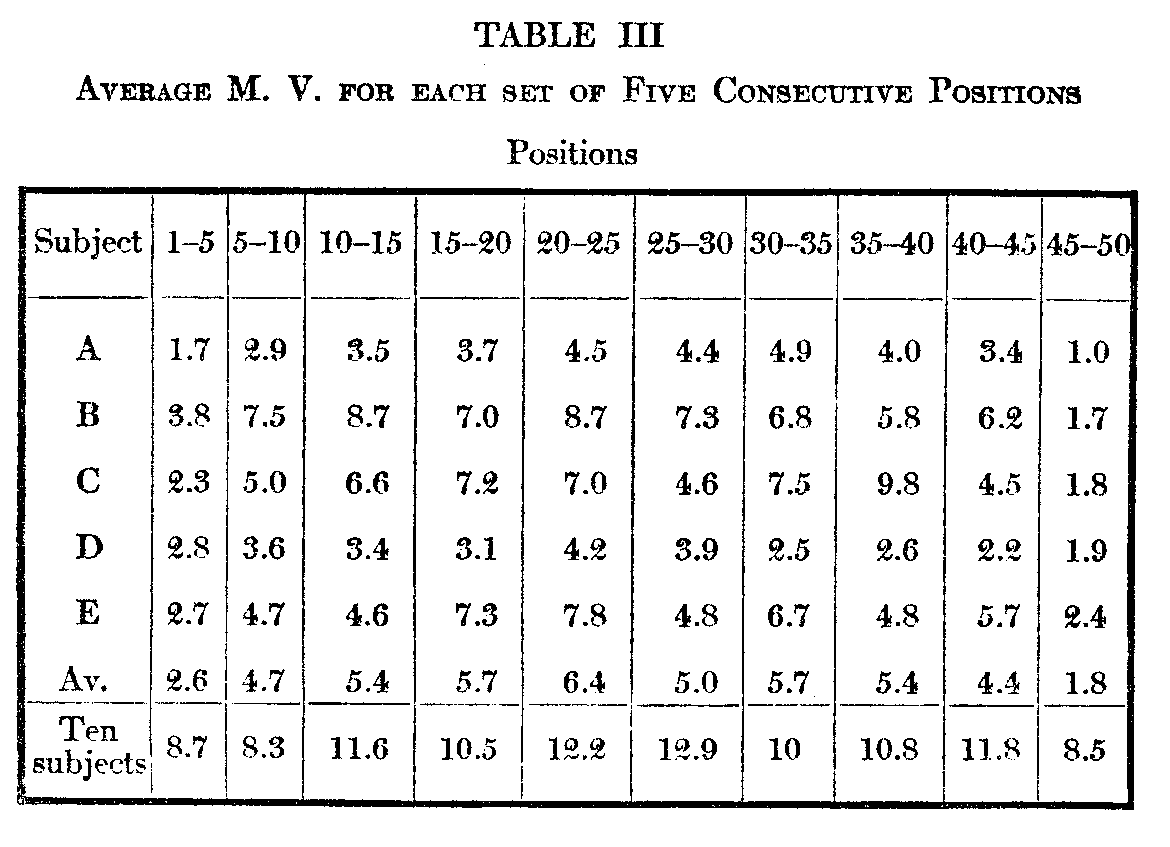
( 524) middle five judgments are respectively 24.6 and 5.7 as against 25.6 and 12.4. Table III below given a basis for a. more complete comparison of the two variabilities. Each series in Table II contains 50 average judgments, consequently 50 m. v.'s in all. These have been divided into 10 consecutive groups of 5 each. Thus under 1—5 and opposite A we find 1.7, which is the average of the m. v.'s of the five cards which stood highest as a result of A's five consecutive arrangements. Under 15—20 and opposite D is 3.1, the average in. v. of cards 16—2o from the series of five arrangementsb D, etc. Opposite Av. are given the averages of the five subjects for cacti set of five consecutive positions. At the bottom. are given. the aver-age in. v.'s for the various groups of positions as assigned by the ten subjects.
(525)
In examining the portion or this table dealing with the repeated arrangements we find, as should anticipate, that the m. v. increases toward the middle positions and decreases toward the ends. The amount of this increase varies considerably, and constitutes a not uninteresting point of individual difference. In subject A the middle m. v.'s are nearly three times those at the start; in D they are barely half again as much. Individual difference in reliability of judgment seems therefore to be greater in the middle than at the ends. This is what we should expect, for the judgments are more difficult in the middle, and we naturally vary more from each other in our judgment of difficult things than in our judgment of easy ones. Another point of significance is that the m. v.'s are always less at the disliked than at the preferred end, although there is no intrinsic reason why they should be better grounded in memory. This might be in part due to a general unaesthetic series of cards, but it is perhaps generally true that we are surer of our antipathies than of our preferences.
In the in. v.'s of the ten subjects the most striping appearance beyond their greater size is that the increase in the middle and the decrease at the ends is not nearly so well marked as in the repeated arrangements. This is precisely the condition that the memory factor in the repeated arra=ngements would give, but under Table IV will be cited
( 526) reasons against its being due to this cause. It is also to be noted that here the m. v.'s of the disliked end are not smaller than those of the preferred, though the difference is insignificant.
The m. v.'s of the repeated arrangements of subjects A–E are shown according to series in Table IV a.
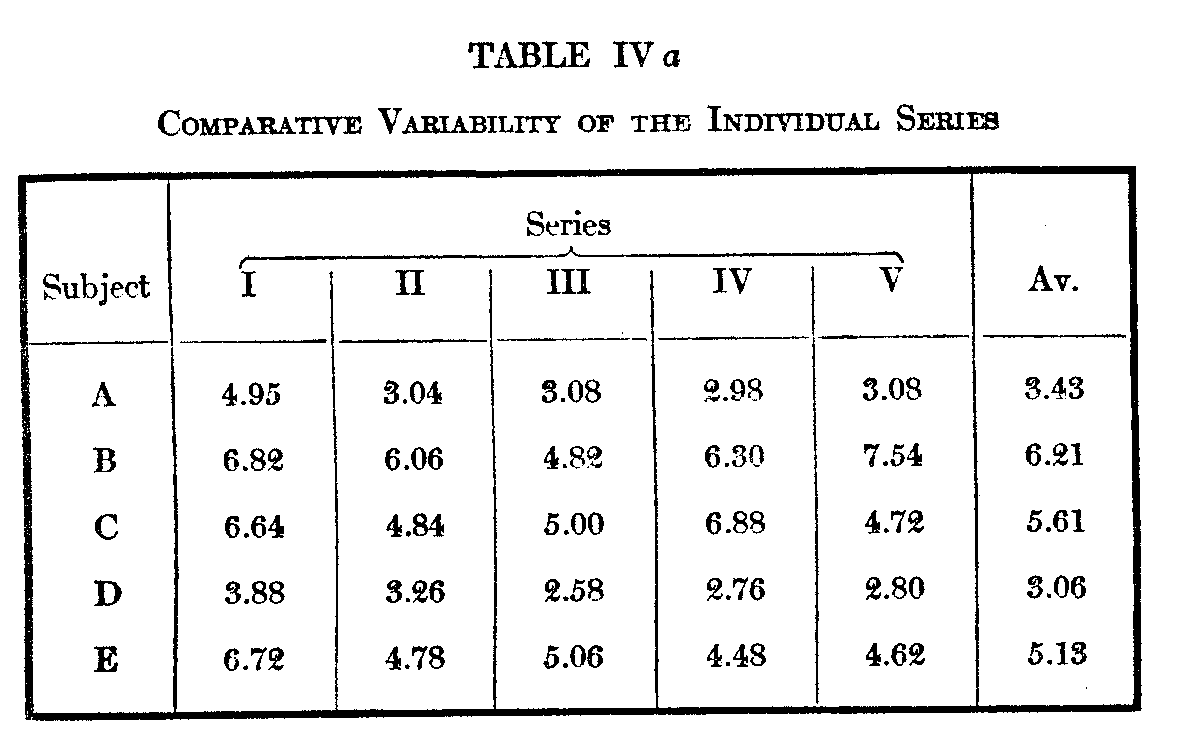
Thus under I–A we find 4.95, which is the aver-age variation of the judgments made in A's first arrangement from the average of the five arrangements made by him ; 3.04 is the variation of his second arrangement, etc. Through this table we can determine what arrangement, if ally, tends to be the most accurate. In subject A the fourth is the most accurate (ay. m. v. 2.9S), in subject B the third, C the fifth, D the third, E the fourth. Now assuming any considerable operation of the memory factor in these experiments, one of two
( 527) things should result. Either the first judgment should set the standard from which the successive arrangements would vary more or less, or, as the memory of previous judgment accumulates, each successive judgment would become more and morethe sum of the preceding arrangements, and the m. v. would progressively decrease. The latter event seems to the writer the more likely, but neither is recorded in the figures, save in so far as the first judgment tends to be a relatively inaccurate one. It is difficult to see in what way the relative accuracy of the successive judgments is distributed differently from what it might be if the successive arrangements had been made by different individuals. They seem to be quite as independent of one another.
Whatever the effect of the memory factor upon the successive series of judgments, those at the ends should be most susceptible to it, those in the middle least. The proper procedure is, then, to examine the variability in the succeeding series according to the position of the cards, and to note if there is any difference in the variability of the successive series according as the positions are high, intermediate, or low. Table IV b gives for each subject the variability of the first five. the middle five, and the last five positions, in each of the successive series. No significant difference appears in the relative size of the variabilities of the middle and end cards, according as the suc-
( 528)
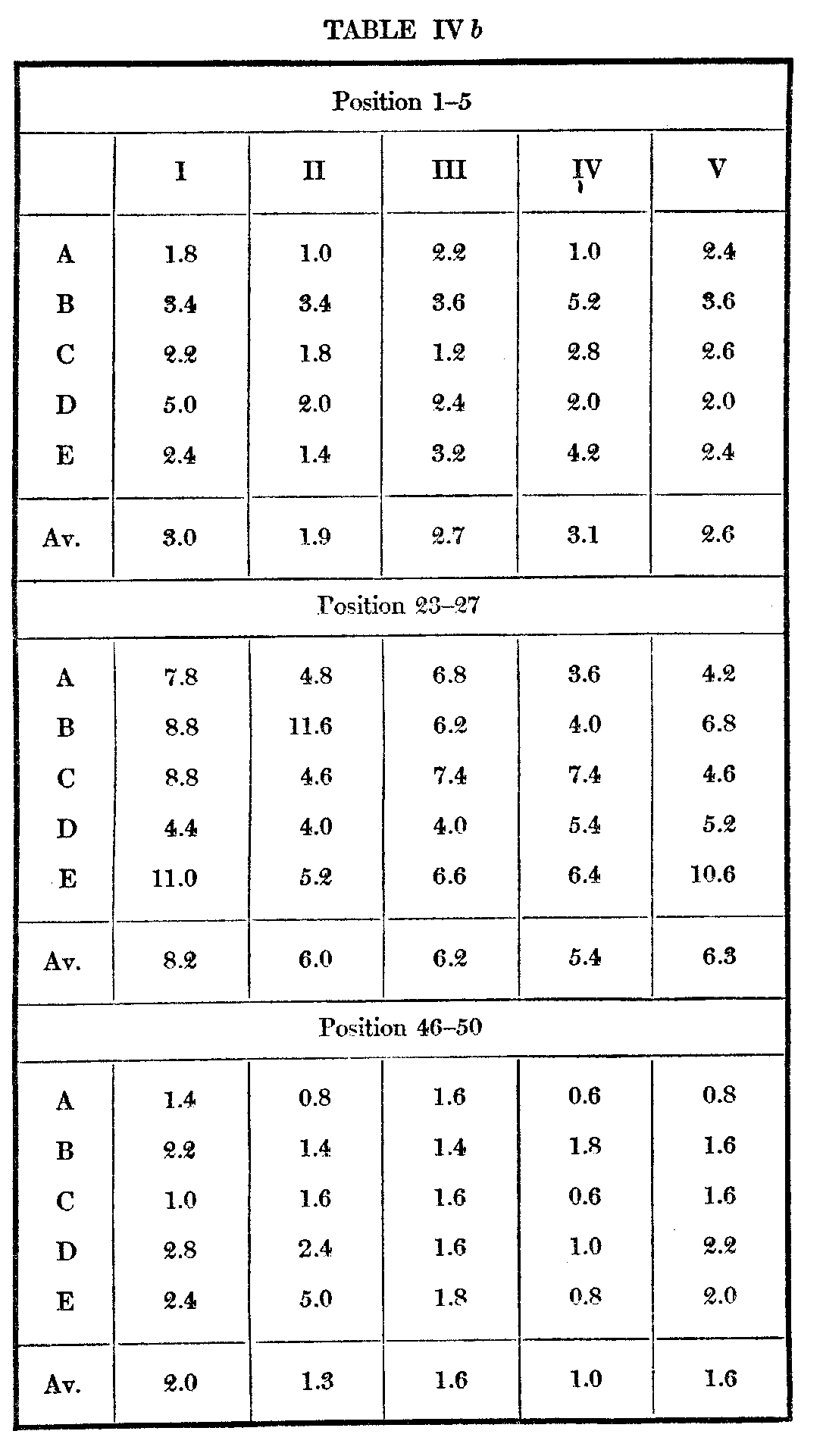
( 529) -cessive series are reached. If memory has operated at all, it must have operated in positions 1–5 and 46–50; from positions 23–27 it is practically excluded. As there is nothing save consistent differences in size to distinguish them, it seems justifiable to infer that memory has in no way made the end judgments less independent than the middle ones. For this reason also, some other explanation must be assigned to the fact that the m. v.'s of the middle and end positions in the repeated arrangements are more different than those of the analogous positions in the individual arrangements by the ten subjects.
In the last column of Table IV a are given the averages of the m. v.'s of each series, the total variability of the five successive series for each subject. There is here a difference of about 2:1, B varying the most from his own judgments with 6.21, D the least with 3.06. The average of all the variabilities is 4.7. Following are the variations of each of the ten subjects from their average :
TABLE V
A B C D E F G H IJ Av.
9.34 10.94 12.98 8.68 11.54 10.34 12.46 9.32 9.12 9.34 10.48
A somewhat significant comparison is afforded between the variability of subjects A–E from the average of the ten, and their variation from their own judgment as given in Table IV a. Those who vary least from their own judgments also
( 530) vary least from the judgments of others. Thus D, whose preferences are the most consistent with her own, also agrees best with the judgment of others. A is next in both (among subjects A—E), and the entire orders agree with 20 per cent of dis-placement. The observations are too few to do more than suggest a general principle, but their interpretation is a rather interesting one. The critic who best knows his own mind would seem the best criterion of the judgments of others. I have elsewhere argued, mainly on theoretical grounds, against the validity of accepting the accordance of a judgment as indicative of its accuracy, but figures like the above are an empirical demonstration in its favor. This matter will be recurred to towards the close of this paper.
With respect to such judgments as those with which we are dealing, the variability of different individuals is seen to be more than twice as great as the variability of different judgments by the same individual. Each individual's judgments form a distinct species of their own, and the opinions expressed are thus in a high degree personal and subjective.
Brief attention may be called to the character of the individual variations themselves. The distribution of the m. v.'s for the averages of the ten subjects has already been given. For the five consecutive judgments of subjects A–E, the m. v.'s are distributed as follows:
( 531)
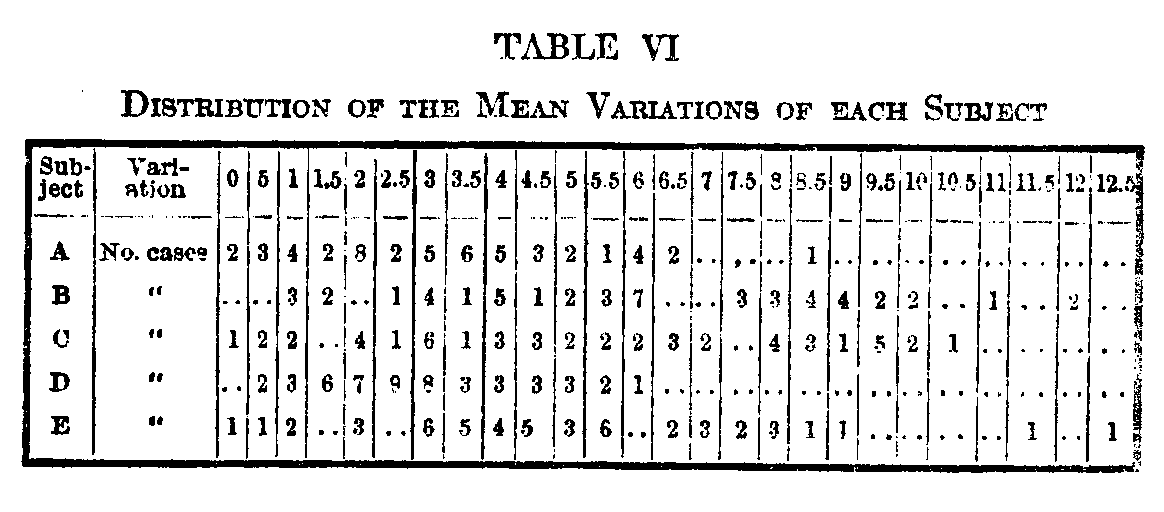
There is a suggestion of species in the distributions for subjects B and C, as though there were a type of card in which the judgments were likely to vary more than in others. The remainder do not show this characteristic. The largest single mean variation is 1 2.8, made by subject E on card 0264, which stands 31st in this subject's series,. The zero cases are from first and last places, with one exception presumably remembered from time to time.
Following are the distributions of the individual variations in the successive judgments. They are
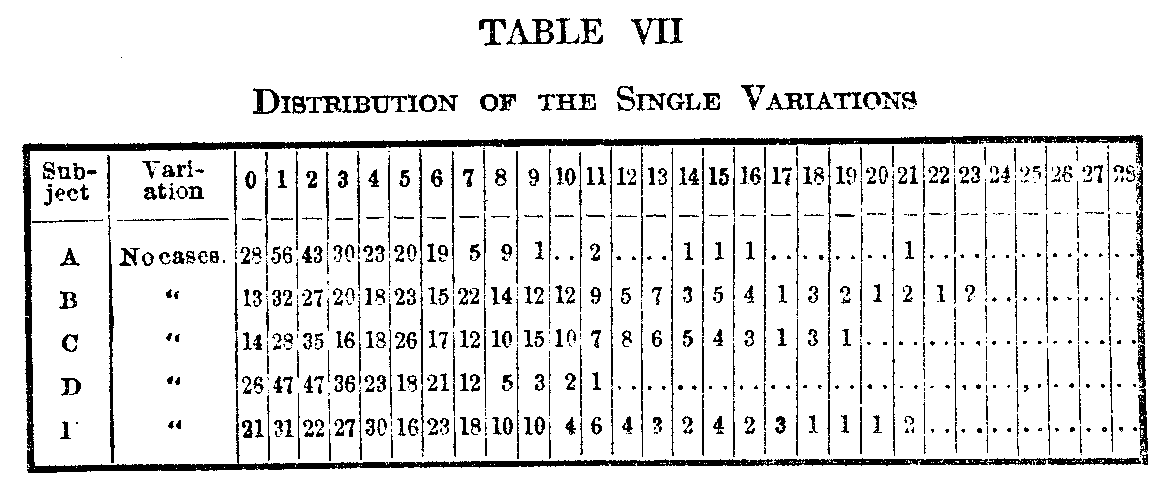
ordinary skew distributions with no striking features. The variability of the single judgment seems
( 532) to be distributed practically according to chance, limited, of course, at the small end.
In a previous study [3] attention was called to the fact that in many consecutive orders the difference in position as indicated by the average did not bear a very strict relation to the reliability of the judgments as given in the probable error. Small differences might exist side by side with small p. e.'s, and large differences with large p. e.'s. On account of the lack of material for empirical analysis the question was merely indicated, but an examination of the longer ranges obtained in the present experiment indicates that the difference between any two consecutive positions is not given in the averages and p. e.'s or even in the entire distributions, but that some refinement of the treatment is necessary.[4]
( 533)
Let us consider more in detail the following portion of our results, positions 21—25 in the records of subject E. The grades here assigned to the cards in 21st—25th positions with their averages and m. v.'s are as follows :
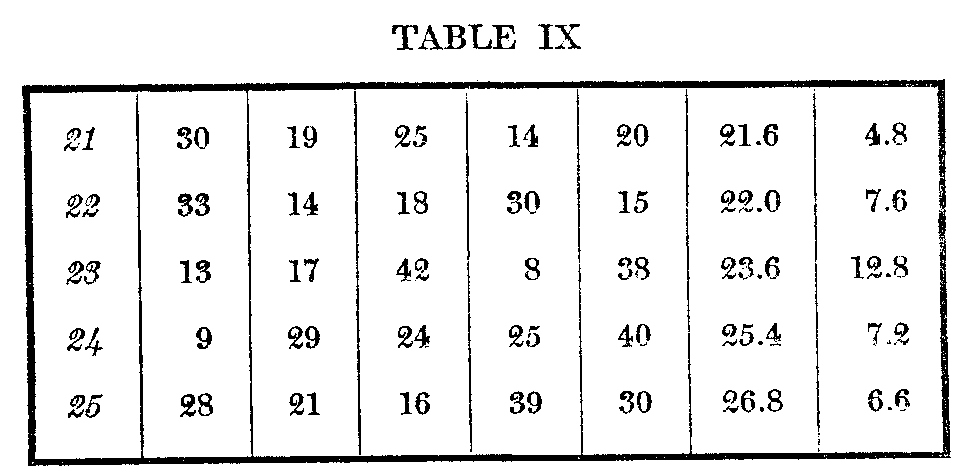
The weakness of the unsupported average and probable error as measures of the difference between two consecutive objects lies in the fact that they take no account of the coincidence of the grades which form them, and which ought to he a most important factor in the situation. Suppose, for example, we wish to determine E's attitude toward the cards whose averages place them 22d and 23d on the list. Out of the five judgments we see that in three cases, in two of a considerable margin, 22 was preferred over 21-, and only the extreme fourth ease gives it a slightly lower place. So much is not fully indicated in the m. v. The point is perhaps better illustrated in positions 24 and 25. In series T and IV there is extreme preference, outside the limits of the m. v.'s for 24 over 25, and the remainders show an almost equally
(534) certain preference for the lower over the higher. The two cards need not really be close together at all ; only now is one markedly preferred, now another. We can get a very different situation without altering average or m. v. in the `lightest, Suppose the coincidence of these grades had been
24 929 24 25 40
25 16 30 21 28 39
We could then. perhaps, say with more confidence that 24 was preferred over 25. At any rate, the two results would have very different meanings, no difference appearing in the average or p. e., which are necessarily the same throughout.
In two consecutive positions from to series with much smaller probable errors the actual coincidence of the grades was as follows :
Av. M. V.
A . . .8 5 5 9 6 2 2 1 5 2 3 1 4 6 2 7 4 4 5 7 4.5 1.7
B . . .7 3 4 2 3 6 7 4 4 510 5 10 5 5 6 3 6 7 1 5.1 1.2
There is .6 place difference in position and the p. e.'s of the averages do not overlap; yet in half the cases the lower position receives e higher grade then the higher. The grades cannot be rearranged so that this happens in more than twelve cases, they can be rearranged so that it happens in only three. The average and p. e. give no hint as to the nature of the coincidences, and their meaning is perhaps sufficient to warrant some special figure to express it.
(535)
Experiments on Color Vision
The apparatus used in these experiments [5] consisted of a series of 28 cards upon which were fixed,side by side, two silk skeins of differing colors. The colors were numbered 2, 4, 6, 8, etc., and. the first card, known as 2-4, bore colors 2 and 4, the next 4 and 6, and so on up to 54-56, when the next bore 56 and then again the first color, 2. The colors thus ran through a complete circle, starting at the reds, and running through the yellows, greens, and purples lack again to the reds. It was not attempted to have the series consist of saturated colors. The steps between the colors composing the pairs are not equal for sensation, and the original object of the experiment was to determine whether measurement by relative position would afford a means for stati ng the differences between the steps in a workable statistical. form. Certain of the results are, however, germane to the present subject. The procedure was to have the subject arrange the pairs in order
the degree of their differences, the pair which differed least being counted 1, the next nearest 2, the most dissimilar pair receiving a grade e 28. Arrangements were obtained from ten subjects, the order, positions, and mean variations being as follows :
(536)
i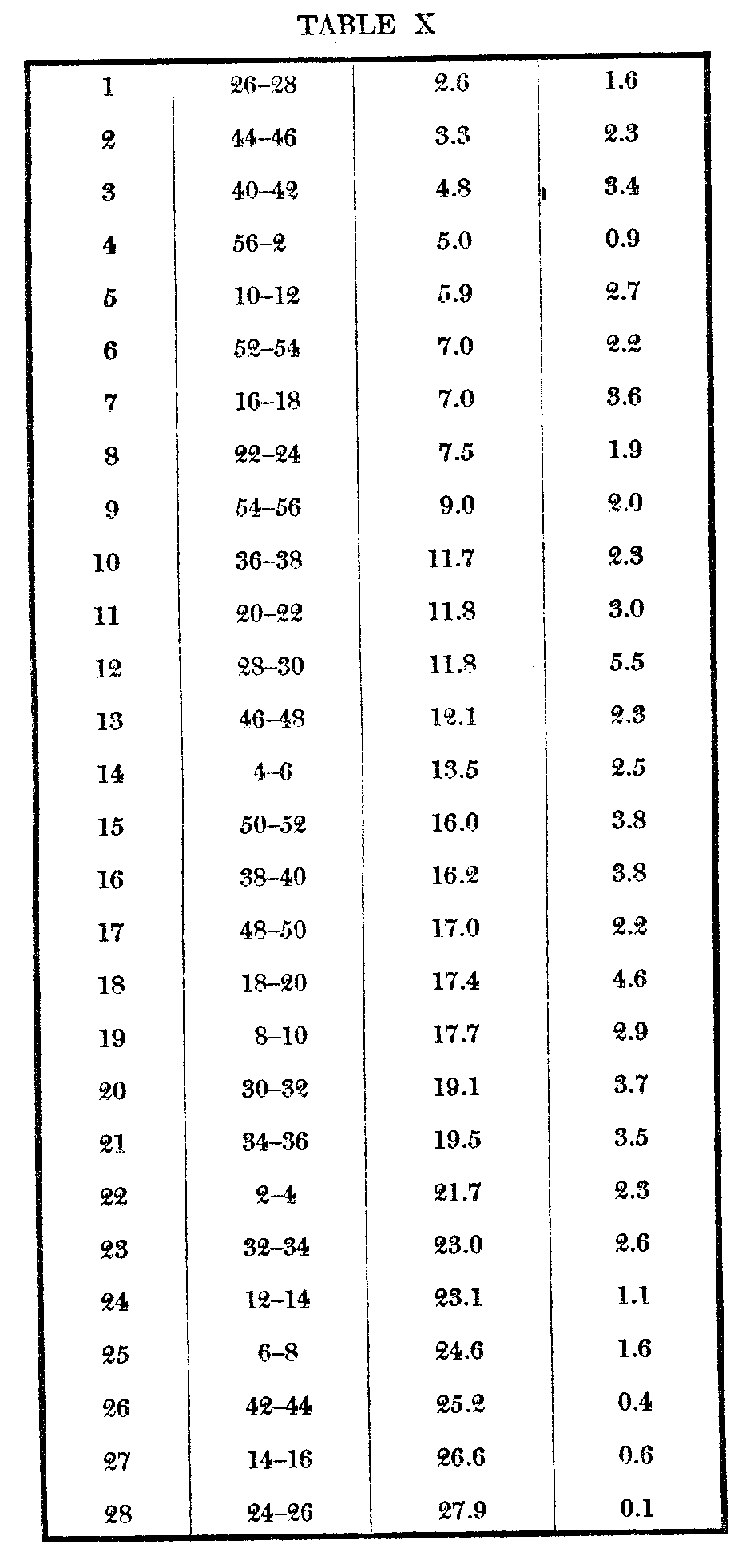
(537)
Color vision being something more objective than preference for souvenir postal cards, we and that the variability of the judgments is much for smaller, the average m. v. of ten individuals for 50 postal cards being 10.8, and for estimations of the color differences but 2.4. The individual variations of each subject are distributed as follows:
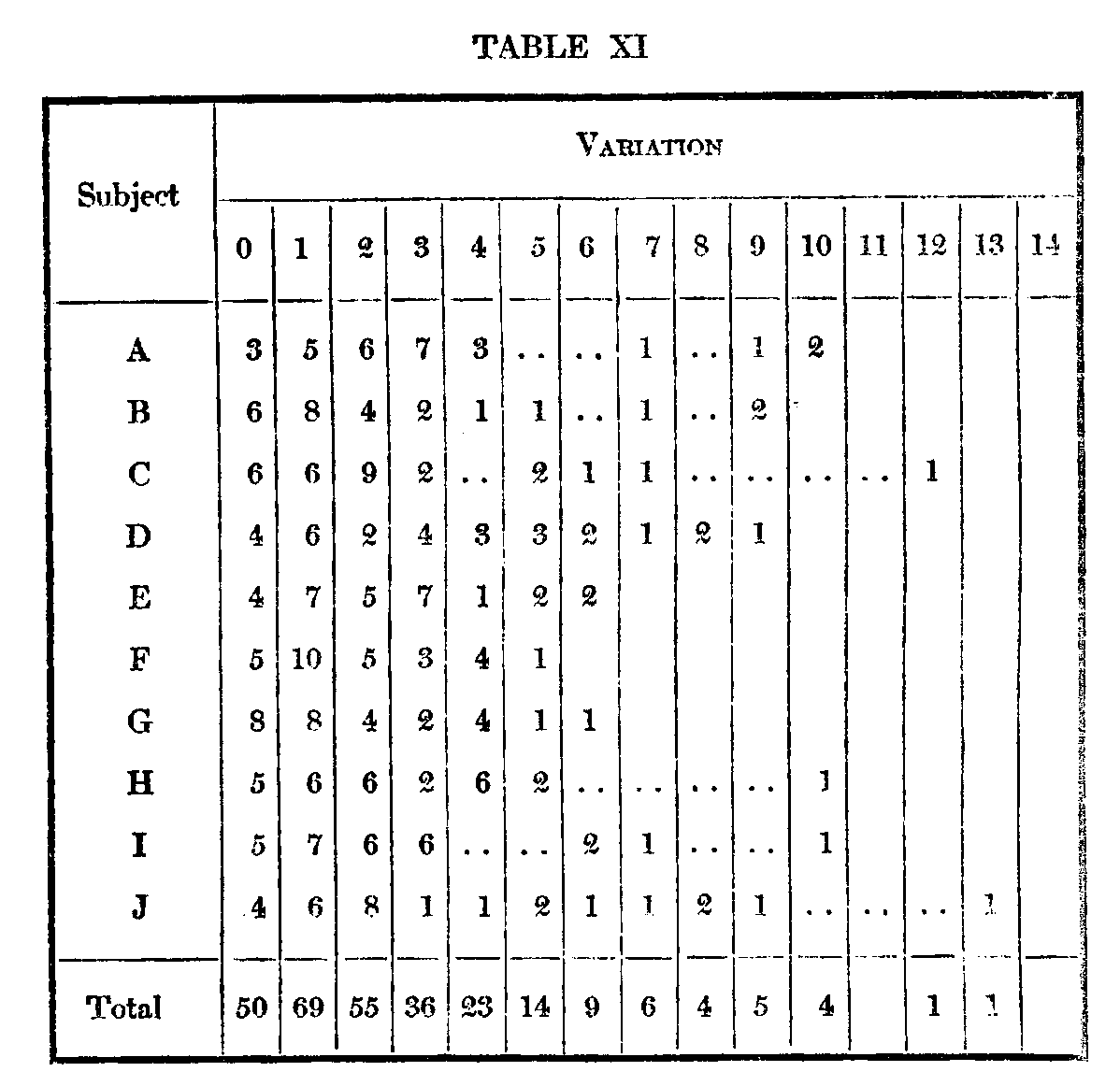
There are six cases, two for A, one for C, and three for J, in which a pair is placed in a position differing from the average by more than three times the in. v. If such cases as these are not due
( 538) to chance, they demonstrate individual differences in color vision similar to those obtained in Henmon's experiments.[6] To make a rough determination of how far they night be due to chance, seven of the subjects arranged the series once more, These included subjects C and J, but it was unfortunately impossible to obtain another record from All of the divergences appear explicable as a result of chance. However, in calculating the m. v.'s of each subject in the two successive arrangements, the m. v.'s of each subject from his own judgment were considerably smaller than the mean of his variations from other subjects, the figures being as follows:
TABLE XII
Subject C D E G H 1J
Av. var. 2. succ. j. . 0.89 1.8 1.7 0.98 1.3 1.3 1.8
Av. var. j. 6 oth. ind. 2.3 3.3 2.3 1.7 2.4 2.3 3.2
There is still evidence of separate species in the judgments of each subject, The peculiar correspondence above noted between the amount of variation from one's own judgment and from the judgment of others appears here as in the postal cards. Between the two orders of Table XII there is 14 per cent of displacement ; the more constant judges are the more accurate. As the objectivity of the experimental material increases, we should expect this correspondence to be closer.
( 539)
Experiments with Weights
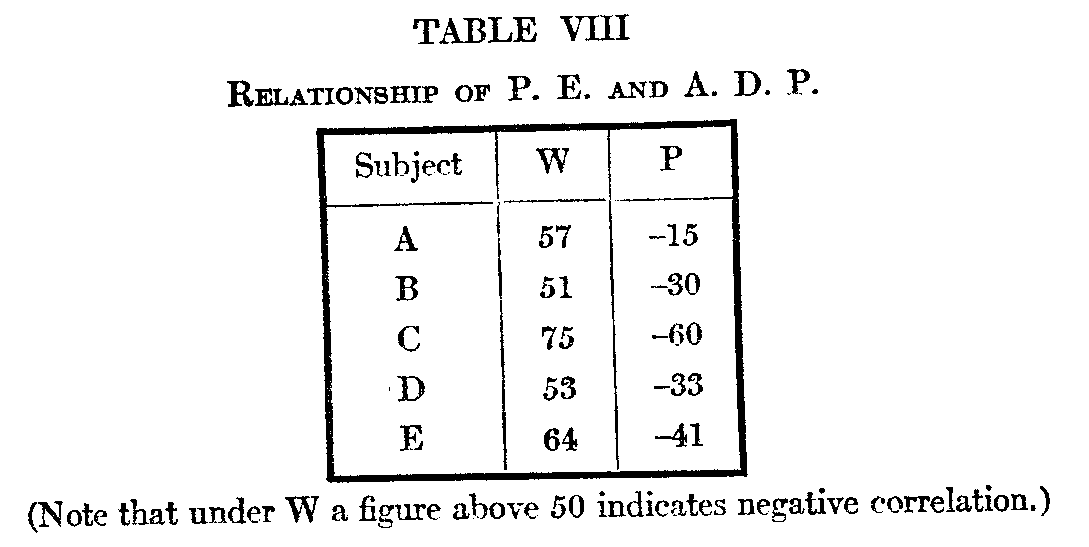
It seemed best, for comparative purposes, to supplement the foregoing observations with. series of experiments in which the actual. differences should be capable of determination strictly objective methods. Weights are probably the most suitable material for this purpose. The apparatus consisted of six weights, 51, 53, 5.5 57, 59, 61 grams, respectively.[7] The weights were made of dead black pasteboard boxes, 1 3/16 x 3 1/8 x 2 1/16, filled with lead and cotton to the required heaviness, and sealed. In the experiments the long axis of the weight was always toward the subject. The observations include 100 arrangements of the weights by one subject, and 10 arrangements by each of ten subjects. Of the subjects, G—J were normal individuals, the remainder being male patients in the hospital. Subject A is a man of 65, whose mental defect is a mixed paraphasia and object blindness. At the time of the experiments he could read and could name letters almost normally, but could not name objects, though they were recognized. Memory was much impaired. He co-operated conscientiously. B, aet.52, is an early stage of general paresis, mildly euphoric. He co-operated willingly, but went at the test in a quick hit or miss fashion. C, aet. 72,
( 540) is a convalescent from a third attack of depression. Co-operated willingly, hut showed a constant error in the shape of a tendency to leave the weights in the random order in which they were placed before him. D, aet. 64, manic-depressive, one previous attack of depression, at present mildly exhilarated. Co-operated willingly and conscientiously, but made frequent pauses between the arrangements on account of “fatigue." E. aet. 38, first attack of manic-depression, mixed phase, mildly exhilarated at time of experiment. Showed same tendency as C in leaving weights as at first placed. F, aet. 32, practical recovery from fourth attack of depression. Interested in experiment, and co-operated best of any of the patients, also doing the test exceptionally well. One other subject, a depression, actively lost interest after four trials, and failed to co-operate further. Each patient was held to a fixed system of procedure, analogous to that adopted by normal subjects. Only F would move the weights of his own accord, the others merely gave their judgments. The detail of their results qua from abnormal subjects I hope to discuss at some future time in connection with other observations. The data from the nor-mal and abnormal subjects are quoted separately. As will be seen, two of the patients do normally, one exceptionally, well, while the remaining three do rather poorly. On the whole, there is nothing in the results to indicate a distinct species of per-
( 541) -formance in the abnormal subject as a class. The general average is probably as valid for present purposes as one from ten normal subjects.
The following tables give the results of 100 arrangements by the single subject:
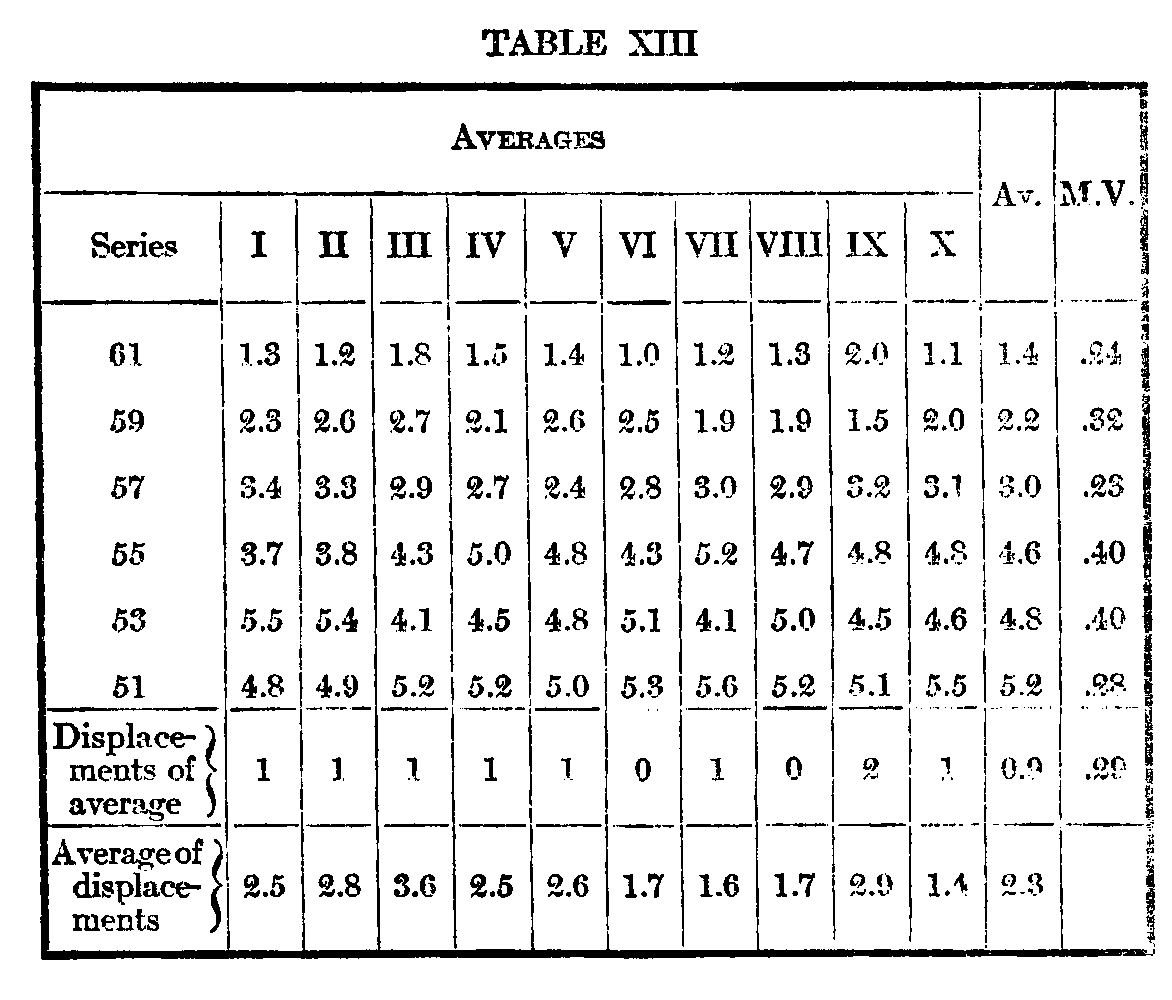
Each column contains the average of a series of ten single arrangements. It will be noted that in only two cases out of the ten does the average order correspond with the objective one. Although the general average of the hundred arrangements gives the objective order, yet the displacements in the single series are hardly distributed according to chance. The fifth weight, 53, stands fifth with a position of 48 in the general average, but in five
( 542) series it stood above 55, in two below 51, and in only two cases did it stand in its proper position, thus accounting for seven out of the nine displacements of the averages of the series. In four of- the seven cases, namely in series I, II, 1V, and VII, the negative difference lies outside the limits of the probable error. VII is particularly striking on account of its high reliability throughout.
As the average should theoretically give the correct order no matter how poor the individual's judgment, the average of the displacements of each individual arrangement from the objective order is a better measure of difference between the accuracy of the successive series. The m. v. of the average order should also afford a measure of discriminativeness. According to both these measures the successive series show considerable practice, the average of the second five being a little over .two-thirds that of the first five. The drop is unusually sudden. It may be observed that the displacement of the average and the average of displacements for the individual series are only moderately correlated within five displaces of their respective orders, or 11 per cent. We are here afforded an opportunity for examining empirically the accordance of an individual series with the average as a. measure of the relative: reliability of the successive series. As the average orders in the individual
( 543) series depart from the objective order, the method does not show up well. Between the accordance
of each series of ten arrangements to their average, and the average of their displacements from the objective order, there are 20 displacements, 44 per cent ;between the accordance of each series to their average, and the size of the m. v. in each series, there are 17 displacements, 38 per cent.[8] The mean variations of each series of ten arrangements from their averages (i. e. the m. v.'s of the averages in the preceding table), are. given below.
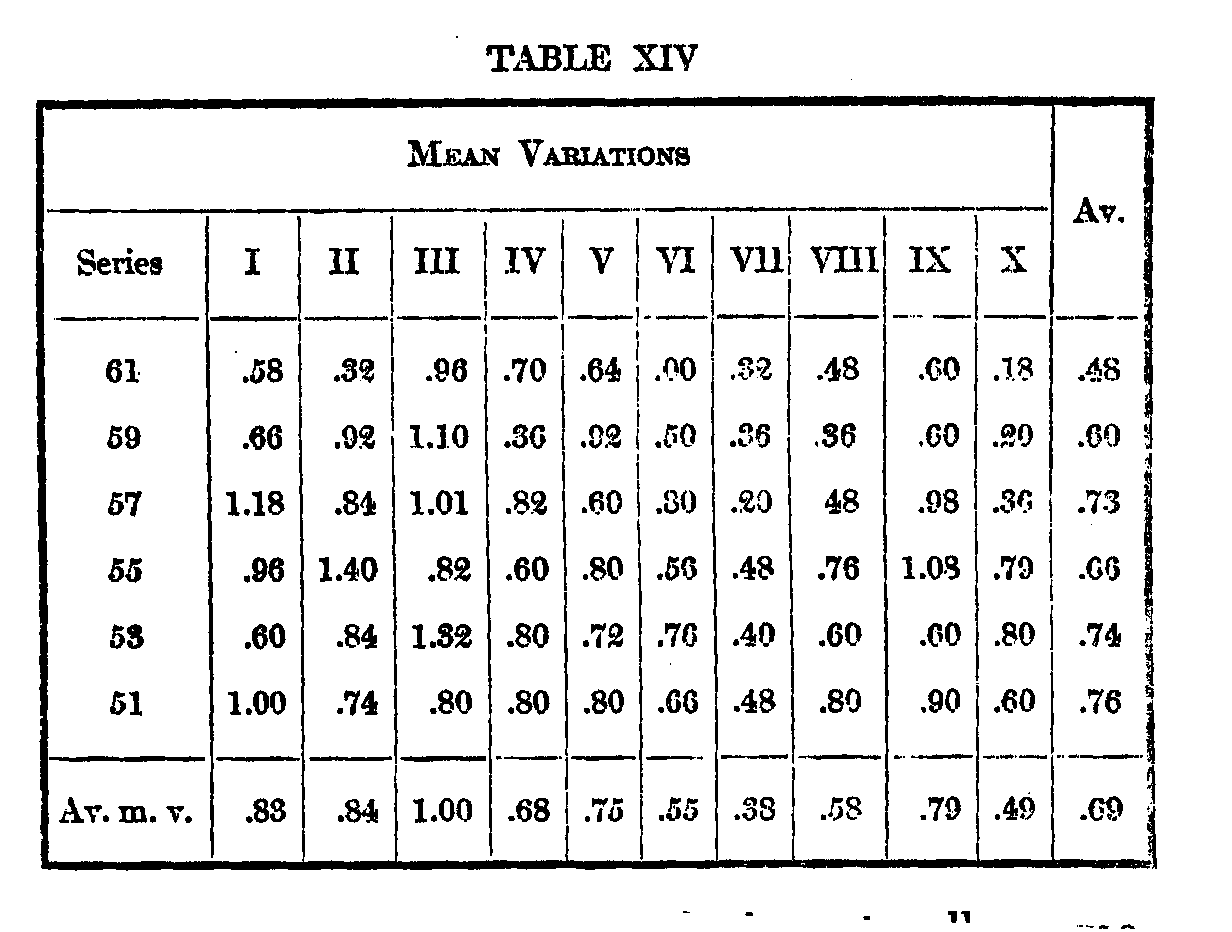
The average of the m. v.’s is naturally some-
( 544) what larger than the m. v. of the averages, as given in Table XIII. It will be noted that the psyehophysical relationship plays little part in these results ; the difference between 51 and 53 should be greater than that between 59 and 61, but so for as can be judged from the results. 61 is more easily
distinguished from 59 than 53 from 51. This is surprising, as the one hundred arrangements ought to he sufficient to bring out such a difference. The m. v.'s of the averages, as given in Table XIII. are smallest at the ends, as they arithmetically should he; but the averages of the m. v.'s, in Table XIV, seem to increase as the weights become smaller.
We may now compare the variation of the single subject through ten successive series, with the variation of ten different subjects through a single series of ten arrangements each. The results of these experiments are summarized in Tables XV and XVI.
The figures present the same general characteristics as those in Tables XIII and XIV. The single subject has varied from his own judgments a little less than the ten subjects among themselves, but this is in part due to practice, which brings down the m. v. If we take the m. v. of the first five series in which practice is not evident to any marked degree, and compare this with the variation of the four normal subjects, we see that the single subject has varied from himself rather more than the four normal subjects among themselves.
( 545)
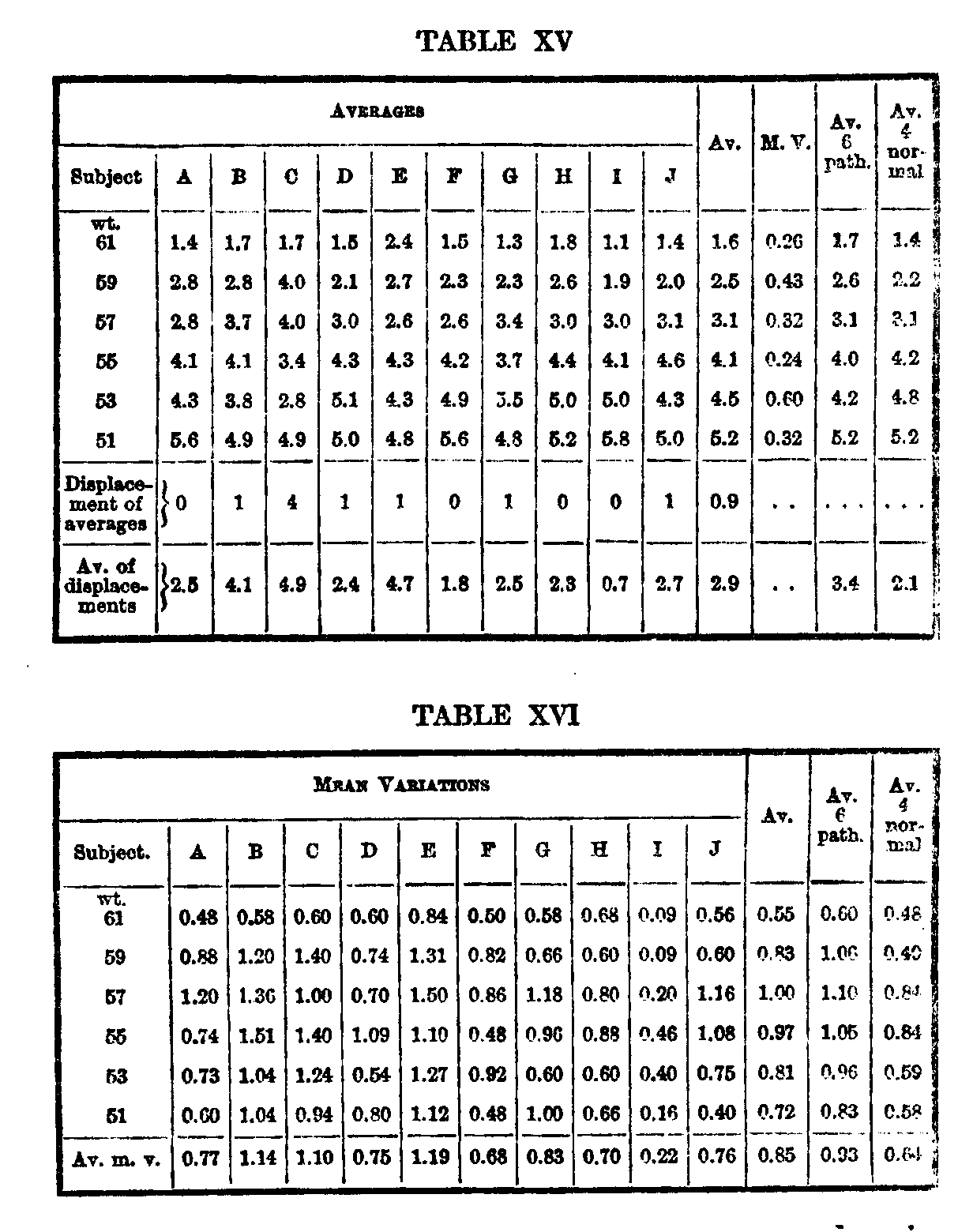
The figure for the single subject is .82, for the six patients it is .93, and for the four normal subjects .64. This is anomalous, for the variation of an individual should only approach the limit of the variability of the group and not exceed it.
( 546) Nevertheless, a striking contrast is formed to the relative variations in the repeated judgments of the postal cards, where each subject's judgments were a distinct species of their own,
In Table XV the record of subject C contains two very coarse deviations from the objective order. There is a remarkable overestimation of 53 and a lesser one of 55, while 57 and 59 have correspondingly low positions. It may be remembered that this subject showed a tendency to leave the weights as they were put before him, and in random arrangements 53 would ordinarily occupy a position higher than its objective one, 59 a lower. But so would 51 and 61, which are un-affected, Subject I underestimates 53, J overestimates it. Altogether, 53 is seen to have a very peculiar behavior.
Comparing, as in Tables XIII and XIV, the average of displacement with the average m. v., we find between them four displacements, 9 per cent. The order of discriminativeness of the ten subjects as measured by the accordance of their individual averages with the average of the ten, gives 14 displacements from the average of displacements and 15 from the size of the average m. v., 31 per cent and 33 per cent respectively. The displacements of the two middle weights, 57 and 55, from the average of displacements are 11, or 24 per cent instead of 31 per cent, for the whole six weights. This result thus agrees strikingly
( 547) with the result for the single subject. The final average order being correct in both cases, it would seem that, empirically, the number of displacements of an individual order from an average gives a better idea of its relative correctness than the precise arithmetical amount of its deviation from this order. It may then also be used in cases where there is no objective, only an average order, as in judgments of mental traits.
Evidence of the psychophysical relationship is again absent ; 61 has a much smaller m. v. than 51, while those of 59 and 53 are practically equal. The m. v.'s are here largest in the middle, as they should be.
Conclusion
We have thus made a brief study of variability in three classes of judgment; first, the highly subjective feeling of preference for different sorts of pictures, second, the more objective judgment of color differences, and finally of a type of judgment whose accuracy could be readily measured by objective means. It has appeared that in the first class the judgments of each individual cluster about a mean which is true for that individual only, and which varies from that of any other individual more than twice as much. as its own. judgments vary from it: that in the second class, with the colors, the variability of the successive
( 548) judgments and those by different individuals markedly approached each other, but still preserved a. significant difference ; while in the third class, with the weights, we found that there might be even an excess of the individual variability over the "social." This comparison seems to afford, to a certain extent, a quantitative criterion of the subjective.
In objective fields those who vary least from their own judgments are, in the absence of constant error, those of the most reliable judgment; indeed, the constancy of our own opinions among themselves seems to be more important than their agreement with the standard of others. It is noteworthy that those who vary less from their own judgments are more likely to vary less from the judgments of others in the cards and colors than in the weights ; it has been shown that this can-not be ascribed wholly to the small ranges with the weights.
It has again appeared in these experiments that even in those fields that we might ordinarily term most strictly objective, there are often certain relations between compared stimuli that are constant and peculiar to the individual. The same phenomenon appeared in Henmon's work on color-differentiation, two pairs of colors not necessarily standing in the same relation to each other with two individuals. The writer also observed it in experimenting with sounds of language, there oc-
(
549) -curring a constant tendency to hear certain sounds rather than others,
which differed with the individual. This is, however, most difficult to
understand with our weights, for it would seem to indicate that the differences
were not only of kind, but also of degree. The situation is not one that could
be readily accounted for by displaced centres of gravity. This peculiar
phenomenon, for which sensation habit is perhaps as good a term as any, is one
that stands in much need of special and accurate investigation.