A Statistical Study of Literary Merit with Remarks on Some New Phases of the Method
Frederic L. Wells
I. THE ORDER, POSITIONS, AND PROBABLE ERRORS OF TEN LEADING AMERICAN AUTHORS
The practical value of the statistical method in the measurement of a mental trait rests upon the hypothesis that such value of this trait as is worth measuring in any individual is significant for a certain group of persons as it impresses itself upon that group, and only in so far significant as it thus impresses itself. This is what the method measures. Unrecognized merit may exist, but it is also likely to be inefficient merit, which is not merit at all in any legitimate sense of the term. We must finally assume efficiency to be in proportion to its influence. This would work injustice only where such influences were unaccounted for, or accounted for to the wrong source, and in such determinations as these this factor is certainly, if not indeed always, negligible. The measure of influence is the ultimate criterion of efficiency.
While the data of the method are based upon introspection, yet they are dealt with in such a wholly objective way as at least to measure, if not indeed to largely remove, the invalidities usually traceable to this source. Just as the biologist cannot make a certain measurement on all individuals of a given species, so here we cannot determine the effect of our objects on all the community. We need not, however, select so much at random as is usually advisable for the biologist, but we can select those individuals whose judgments are the least likely to vary, that is, those best informed on the subject, just as the biologist would select as assistants those individuals who gave him the smallest variations in measuring the same object. We might also regard the judgment of each grader as a new measurement made with the same instrument. In the absence of constant error, we suppose those measurements the most accurate which vary from each other least. We should find that persons who had never heard of our 10 American authors would grade them almost by pure chance and that persons of limited knowledge in this respect would vary a great deal, but when we come to those who have made a special study of this group there is but little variation, and it is their judgment that we therefore regard as the most valid. As we ascend the scale, constant deviations, mainly of a chronological and geographical nature, are introduced, and this precludes determinations of absolute validity. It is not these that would be of most use, however, but the knowledge of how the series of graded objects has influenced a certain particular group. From this point of view the method is as much a measure of the judges as of the judged.
( 6)
In these experiments we get a direct measure of the relative extent to which the authors have impressed themselves upon the group which we are studying. In so far as this is a representative group, we get a measure of the extent to which they have influenced the community represented, and a determination based, from this viewpoint, upon entirely objective facts.
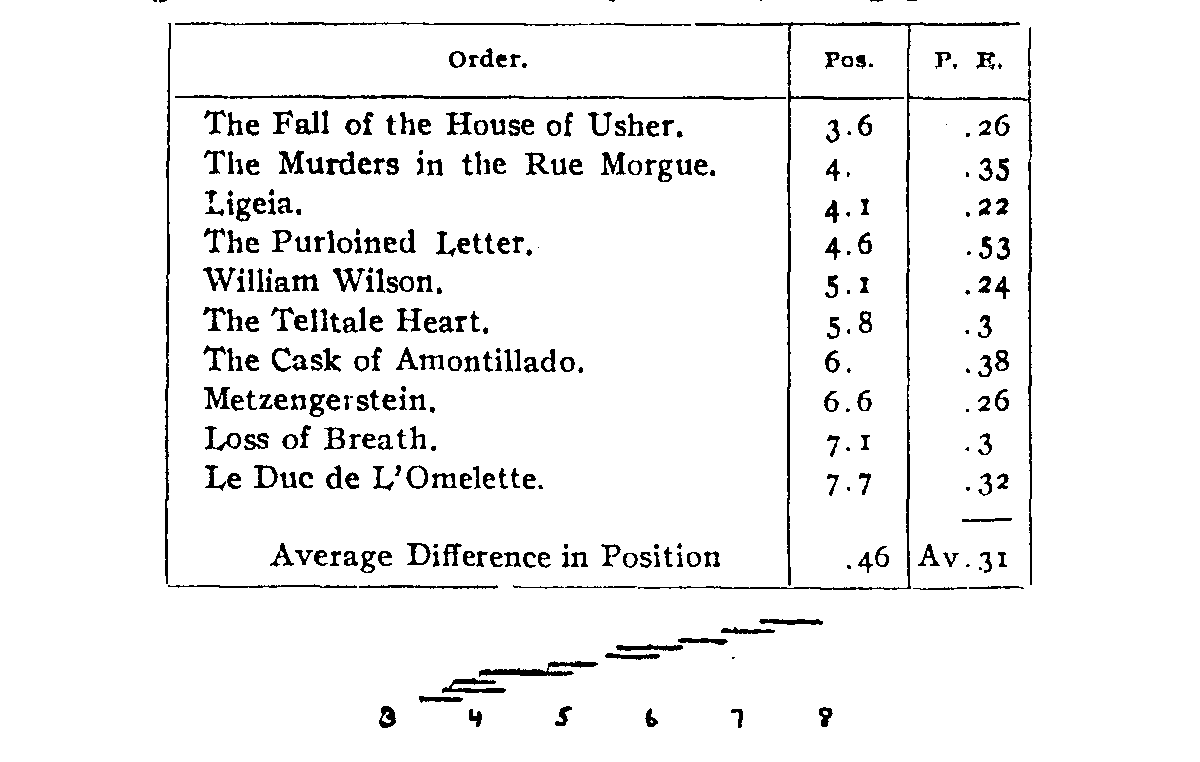
The writer's first experiment by this method along the lines of literary criticism dealt with short compositions by a single author, the arrangements being made by 40 women undergraduates. Ten stories by Edgar Allan Poe were graded in order of preference, the order, positions, and p.e.'s, together with the graphic representation according to the scheme devised by Cattell,[1] being given below.
On account of the limited training of the graders the m.v.'s are considerable compared to those to be subsequently discussed. The differences in position are also much smaller. Working by the method of % of like signs it was not possible to discover any correlations in preference, positive or negative, that might not as well be ascribed to pure chance. This seems rather surprising, as one would naturally have expected relative preferences to be the same within types of stories, that is, one who disliked Loss of Breath should also dislike Le Duc de L'Omelette. But such slight relationships as did appear seemed to be rather between stories relatively unrelated by ordinary critical standards, as positive between Loss of Breath and William Wilson, negative between The Purloined Letter and The Cask of Amontillado, etc.
These results appeared to indicate that the standards of literary criticism erected by accepted critical scholarship would bear experi-
( 7) -mental examination. Aside from the intrinsic interest of determining relative positions in the group tested, it seemed desirable to analyze so far as possible the precise standards upon which such judgments were based. Accordingly the experiment whose results form the raison d'être of the present study was devised. It is not, however, to be anticipated that the introduction of a scientific method into this field should contribute markedly to the principles of accepted critical procedure; the main function of literary criticism having hitherto been to serve rather as a convenient vehicle for individual expression than for the empirical determination of actual literary relationships.
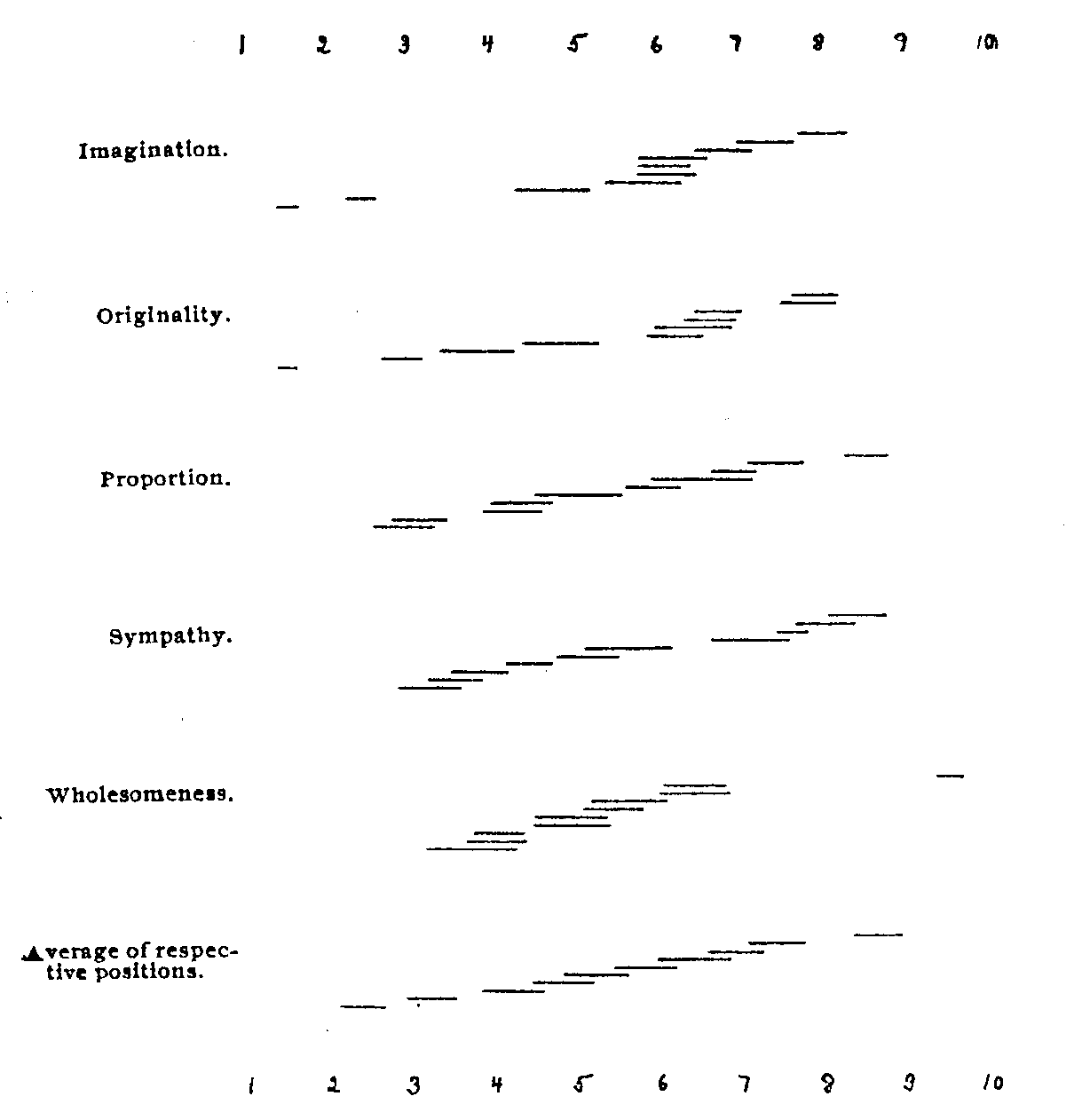
Ten American imaginative writers were selected for study, these being presented in alphabetical order, Bryant, Cooper, Emerson, Hawthorne, Holmes, Irving, Longfellow, Lowell, Poe, Thoreau. They are presumably all in the first 15 of their class. These were graded first in respect to general literary merit. They were then graded in respect to their possession of ten literary qualities. These, also in alphabetical order, and with the abbreviations by which they will subsequently be designated, were Charm (Ch), Clearness (Cl), Euphony (Eu), Finish (Fi), Force (Fo), Imagination (Im), Originality (Or), Proportion (Pr), Sympathy (Sy), Wholesomeness (Wh).These lists were not determined by any standard method but by a literary critic in ordinary consultation with the writer. The terms are in the main technical terms of literary criticism and there seems to have been no great difficulty about their interpretation. The grading was done at a meeting of the English Graduate Club at Columbia University, the work occupying from 35 minutes to 1 hour. One of the graders was the critic above mentioned, the remainder belonging, with 2 or 3 exceptions, to the graduate student group. There was a remarkably small amount of invalid data, principally confined to such lapses as grading the same author 3rd and then again 7th. The present results are derived from 20 records.
Of course in so large a number of separate distributions as that under consideration (110), the probable incidence of certain forms by pure chance is not inconsiderable. While in general they approximate the normal distribution as closely as could be expected in the limited number of judgments, yet it may be worth while to call attention, with special reference to species, to some of the more marked deviations from the normal, where the factor of chance, which, of course, is itself always measurable, does not seem to play a prominent part.
This is perhaps the phase of the results most interesting to students of literature. For example, the fact that VII (Bryant) has a distribution of such marked bimodality as to be practically with-
( 8) out the range of chance deviation from the normal, is perhaps not without critical interest. It has been suggested that these two groups might have a certain geographical distribution, the relatively higher grades coming from New England and neighboring states. It is now impracticable to verify this supposition, but there is nothing inherently improbable about it, and such theories are, of course, experimentally verifiable. I am rather distrustful, however, of the value of explanation for its own sake and representing a personal opinion. We shall perhaps do well to remember that we know just as good reasons for many things that are not so as for things that are, and when the history of our present thought is written it will probably be found that we have explained to our complete satisfaction quite as many of the former as the latter.
There is little ground for supposing different species in the remainder of the general merit grades except perhaps in the case of VIII (Thoreau), whose grades fall with almost equal frequency among the last 5 positions. The three most markedly bimodal distributions in the quality grades are those of II (Poe) for Charm, and I (Hawthorne) for Clearness and Sympathy. In 17 cases the same author receives grades in first and last place, though in only 2 cases is there a grade in every place, namely, in IV (Lowell) for Sympathy and X (Cooper) for Clearness. The most variable distribution is that of III (Emerson) for Proportion with a p.e. of .61, and the least variable are those of II for Imagination and Originality with p.e.'s of .11 each. There are naturally many distributions that on their face are bimodal, but the probability of their occurrence by pure chance is too great to warrant their acceptance as evidences of species in the judgments. On the whole, the opinions seem to concentrate about a common centre rather than to form groups.
If the distributions were governed by pure chance, they would always approximate to 2 grades in each place. As the frequencies are not governed by pure chance, but presumably by the probability distribution about a mode, we can roughly determine to what extent the variability we obtain is a true variability for this class of judgments. For example, in the 40 judgments of Poe's stories, it was found that the results from 20 random selections differed but little from the results of the 40. There would thus be reason to believe that the variability found in the 40 judgments was representative of the amount of variability that we might expect to find in dealing with judgments of this sort. It has been suggested that in this method at least, the reliability increases much more slowly than as the square root of the number of cases, and may be more accurately represented by the mean variation itself.
If the factor of memory might only be overcome, it would be
( 9) well worth while to compare with the variability of many individuals the variability of a single individual from the average of his own judgments. This was done by Cattell for a considerable number of psychologists. We should then have a measure of constancy in judgment that would have a not uninteresting psychological bearing. A single judgment is subject not only to error from the average judgment of other individuals, but from the average judgment of the individual himself. Large and small m.v.'s may be the product of variations along either of these lines. We are all probably very much surer of our relative preferences for lobster Newberg and fried oysters than of our preferences for Emerson and Hawthorne; yet these very differences in taste might produce as large an m.v. in one case as in the other.
For some purposes of analysis the median has seemed a better measure than the average. It was somewhat discredited in the results of Cattell, but is of more value here on account of the larger number of measures. The average is here also relatively less valid because the number of possible positions is limited to ten, whereas it was there in the negative direction practically unlimited. In the present results there is almost no distribution in which the author does not receive a grade in either first or last place, and when the grades are banked up against first or last place, the average is obviously too low or too high, probably more so than the median. However, it is of no particular consequence which we use so far as order is concerned, for the two orders are almost identical, the divergences that occur being well within the limits of chance variation.
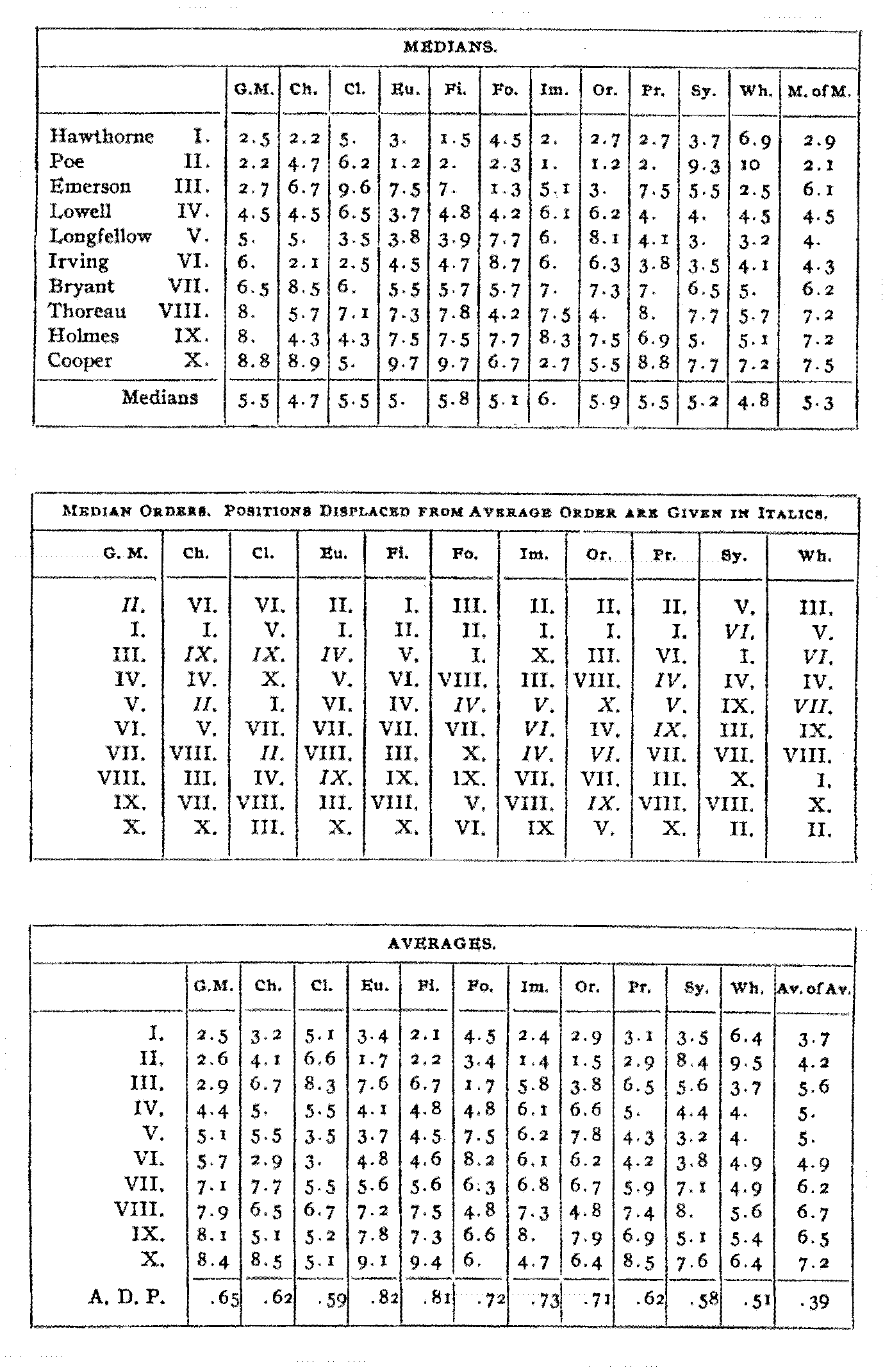
The accompanying tables give the main results of the experiment in the median and average order and position of the authors in general merit and the qualities.
In general merit the writers fall into three groups, separated by considerable distances, three at the top, three in the middle, and four at the bottom. Between the three at the top there is little difference to speak of, between I and II practically none at all. The median of II is considerably higher than that of I, and it is very possible that his true position is higher than I. Such constant error as might result from prejudice would perhaps operate more against II. Each has six grades in first place, and none in last. It is quite anomalous that the differences should be greater in the middle group than at the ends; although the p.e.'s are not of the smallest they fail to overlap at all; the chances are over 16–1 that the order given is correct. The narrow mathematical limits of variability might account in a measure for the small p.e.'s at the ends, and perhaps also for the small differences in position, which are equally striking; but only in a small measure, for this condition does not obtain in the quality grades, nor in
( 10)
( 11)
other relative position work that has been done with even smaller series than 10. Between the positions of VI and VII is another long step, 1.4 between positions, .8 between limits of p.e.'s, and VII again fails to overlap the p.e. of VIII. From here until X's position at 8.4 the steps are about equal.
It is thus seen that we have no man who is so distinctly at the head of American writers as one is found among contemporary Astronomers, Psychologists and Pathologists. It is perhaps a fair inference that enlargement of a group may decrease differences at the top by bringing more of the leaders into conflict. There is no doubt that a certain department of American letters could have been found in which III would have reigned supreme, and the differences between I and II could have been much increased, in either direction, by narrowing the field of literary work to be considered. It is beyond dispute that there would be more disagreement about the order and less about the identity of the five greatest poets of the world than the five greatest poets of France. Such a condition is probably to be expected in all walks of life. There is a limit to the realization of human powers fixed by opportunity and other environmental factors. "Es wird dafür gesorgt," says the German proverb, "dass die Bäume nicht in den Himmel wachsen." If we artificially limited to 140 ft. the height of a tree ordinarily growing to 150 ft., we should find more trees at 140 than at 135. It acts in the same way as any other limitation of a normal distribution, crowding the extreme cases together. This is probably a reasonable alternative to the supposition of genius as a separate group.
Though the peculiar conditions noted above do not generally obtain in the qualities, these present certain other points of interest. In Charm there is a group slightly above the middle position, the increases and decreases from which show nothing anomalous. The
( 12)
( 13) author in first place, VI, is ordinarily noted for his Charm, and the fact that he is so hard pressed by I may mean that he is so noted more than he deserves. He is graded rather for its prominence relative to his own other qualities. Clearness again gives us two positions at the top, VI and V, and widely separated from the next five, who form the largest single group in the results. The p.e.'s are unusually large. It is also peculiar that the lowest individual in the quality III, has also the largest p.e. in it, the only case among the qualities where the last p. e. is not smaller than the average.
Euphony has one of the widest ranges and is among the smallest p.e.'s. The leader, II, and the last, X, are a long distance from any of their fellows, while the remainder fall into two groups, the upper of five and the lower of three, separated by an interval of nearly a place. The distribution in Finish is a composite of those in Clearness and Euphony, there being two leaders, I and II, and a distinct last place, X, as in Clearness, without the closely packed group of that quality. Force again has a distinct leader, III, but the remainder trail behind with no characteristic variations in successive distance. The same is true of Imagination except that there are two leaders, II and I, though the difference between them is itself not inconsiderable. There is a marked group as in Clearness, but here centered at a position lower than the average. In Originality the first four positions, II, I, III, and VIII, are established well beyond the limits of p.e. Then comes a closely packed group of four, and separated from these by an interval of about a place are the two lowest positions. The distribution is quite similar to that of Imagination. Proportion resembles so closely the distribution of Charm that the same may be said of them in essential, save that in Proportion there is not so distinct a grouping. In Sympathy, whose range is also of the smallest, the p.e.'s all overlap save for the considerable break between 6th and 7th positions. In Wholesomeness the first nine are distributed over a very small range, and the tenth—II in general merit—brings up the rear with the largest difference and one of the smallest p.e.'s of the results. The final figure gives the average position and average p.e. of each place in the above qualities, irrespective of the author holding it. The first and second positions are, as a rule, determined with some certainty, as is also the last. In all the remainder the p.e.'s show a slight and very constant overlapping.
The p.e.'s have been calculated by the simple formula advocated in Cattell's Statistics of American Psychologists, i. e., p.e. = (.845 A.D.)/root (–1). They are, as has been noted, probably smaller than is representative of the actual reliability of the determinations. It will be noted, however, that they are quite consistently larger in the qualities than for
( 14) general merit. This may be taken to mean that we really differ less in personal opinion about a general attribute than about its constituents, or that in these constituents there are likely to be smaller differences than in general attributes. Judgment of general merit may be more variable than judgment of special merit, and general merit may itself be more variable than special merit. Under the present circumstances, however, we seem to have a fairly complete list of qualities, of which, on the former supposition, some should be more variable, some less variable than their total. As a matter of fact, the quality grades are all more variable than those in general merit, which seems to point to the latter interpretation as the more valid one, especially when we consider that the average difference in consecutive position (A.D.P.) is in but five cases out of ten greater in the qualities than in general merit. The fact seems to be that the differences are more variable in the qualities; the median difference

( 15)
in position would here be smaller. The extreme p.e.'s are also smaller in the qualities than in general merit. In certain isolated cases, as that of II for Wholesomeness, it seems that judgment is surer than for general merit, but it may also go farther astray, and is usually less accurate than for generalities.
It is a not uncommon observation that we often form judgments for which we cannot give satisfactory reasons, and it is perhaps not less common to observe that these judgments are about as likely to be correct as those for which we can. To this empirical generalization the above figures seem to lend experimental support. We are more accurate in our opinions than in our reasons for them.
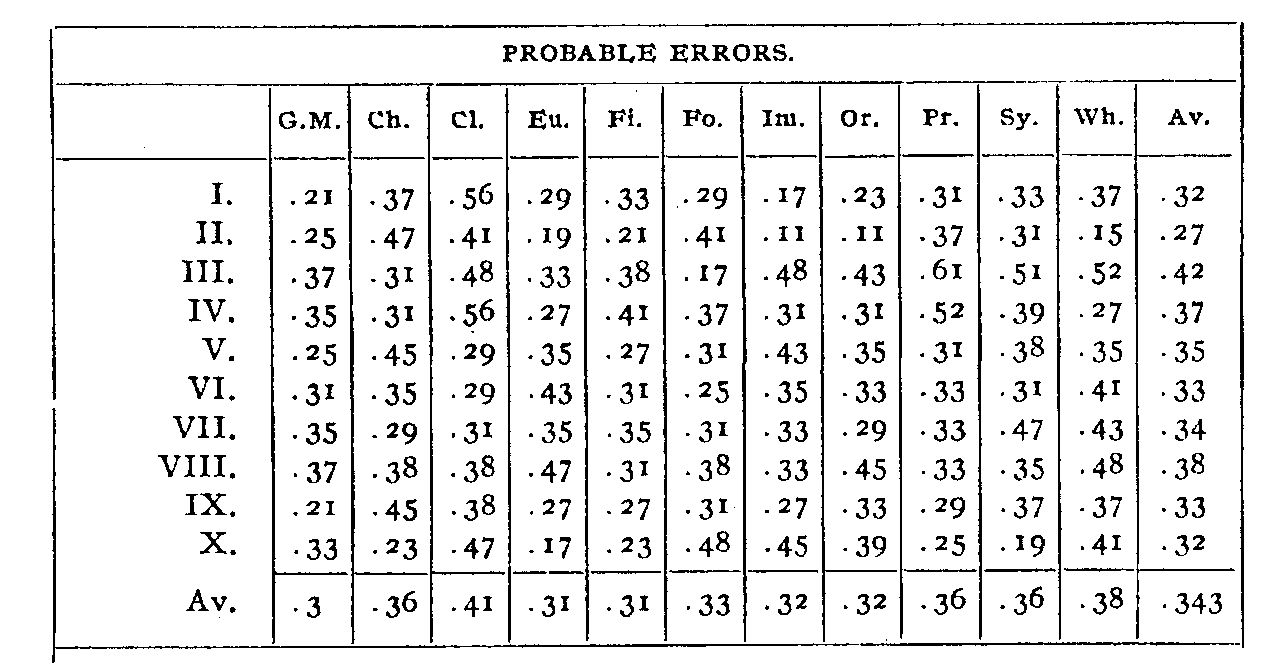
The p.e.'s are of some interest in themselves, quite apart from the positions to which they attach. On a scale of .05 they are distributed as follows:
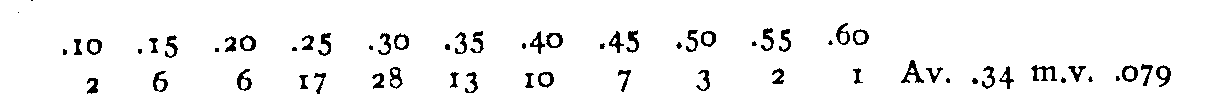
(16) The largest and smallest p.e.'s are, as has been noted, those of III in Proportion and II in Imagination and Originality. The distribution is skewed toward the small end, indicating, if anything, a sort of psychological limit in variability, just as we assume a physiological limit of quickness to account for similar distributions in reaction time. This would probably be determined by the individual's. chance variations from his own judgments. Even if there were complete agreement of the average opinions of the individuals we should not get p.e.'s of .0, because no single measure would give us this average.
The distribution is quite regular, with no surface indications, of species, but analysis makes it rather probable that they exist.. Each of the p.e.'s represents roughly the accuracy with which one of the authors can be graded in one of the qualities. We should naturally expect that some authors would be more accurately graded than others. On comparing the average p.e.'s of the authors' quality grades we find an order fairly distinct, though, of course, itself subject to a large p.e. II is the author about whom, wherever he is placed, there seems to be the least all-round disagreement; the average of his p.e.'s is only .27. On the other hand, there is the greatest discord about his neighbor, III, his corresponding figure being .42. The complete order of accuracy in which the qualities of the authors are estimated is II, I, X, IX, VI, VII, V, IV, VIII, III. As will be seen, this order bears no direct relation to that of general merit, but we do have a logical result in there being the least disagreement about those at the ends of the list. Such a fact indicates that there is no great difference in information about the authors as related to their positions. As it is fair then to assume that we know nearly as much about the last man as about the first, we probably know approximately as much about those in the middle, their higher p.e.'s being due to more marked differences of opinion about them.
A curious sidelight upon this situation is thrown by the fact. already brought out in the last of the diagrams referred to on p. 15. An analogous result is obtained from the average of the p.e.'s taken in respective order. That is, if we average all the p.e.'s of the first positions in the qualities, then those of all the second positions, etc.,. we obtain a quite regular increase at the middle and decrease at the ends. This can not be called surprising in view of the results mentioned in the preceding paragraph, but it is hardly what should have been expected a priori. It is as though we had in these authors. stumbled upon a range, or grouping of excellence in the literary qualities. The artificial limits of the p.c. do not seem to suffice for the facts. This is a result contrary to that given in the positions of general merit, in which differences were greatest in the middle. Inrespect to the qualities, the authors seem to form a group, their relative positions, of course, differing widely for each quality. In respect to the direct general merit grades they can be considered only as part of a group or as three sub-groups. The discrepancy may be accounted for by the wide range in
( 17) importance of the qualities and the lack of correlation between them.
In the same way as with the authors, we should also expect it to be possible to grade certain qualities more accurately than others. Comparing the averages of the p.e.'s for the qualities, we see that this is to some extent the case, though the range is not so large as with the authors. The most accurately graded of the qualities has an average p.e. of .307, the least one of .413, the order being Euphony, Finish, Imagination, Originality, Force, Proportion, Sympathy, Charm, Wholesomeness, Clearness. The size of this average p.e. corresponds generally to the A.D.P. of the authors in the various qualities; where the p.c. is smallest, the A.D.P. is greatest, as we should expect. It would seem almost tautological to say that the accuracy with which differences were perceived would be dependent on their size.
However, this does not seem to be necessarily the case, as is shown in the results of Cattell. We may have equal differences in position with unequal p.e.'s, and equal p.n.'s attached to very unequal differences in position. Though it would hardly make much difference in the upper ten positions, the cases most comparable are those in which an equal number of workers are considered. Such cases occur between Physics-Zoology, Botany-Geology, and Astronomy-Psychology. The relations of the p.e. to the A.D.P. are in these cases as follows:
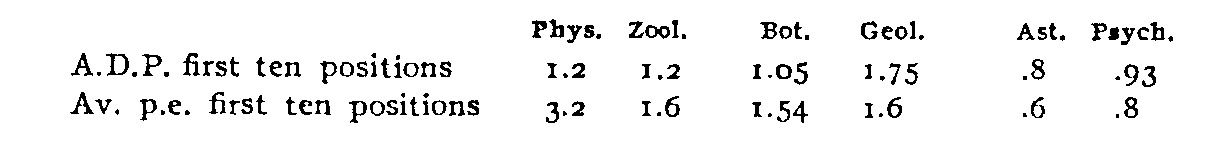
The size of the p.e. seems to a certain extent independent of the differences in position. The A.D.P. of the first ten botanists is less than that of the first ten geologists, but the graders of the geologists are slightly less reliable than those of the botanists. It seems, on the one hand, that individuals may differ more, yet on the other hand it may be impossible to estimate the differences with so great precision. It would hardly be profitable to discuss the conditions of such a relationship save upon the basis of empirical analysis, for which the small ranges obtained in the present study hardly afford sufficient material. The variability of individual gradings might also be an essential factor. It is evident, however, that neither figure alone expresses the sum total of the differences. Professor Cattell has employed a correction for the range, which gives the various p.e.'s
(18) more strictly comparable values. The relationship might also be expressed in terms of the ratio of the p.e. to the A.D.P. This would furnish a rough index of the adaptability of different problems to measurement by relative position. The general ratio of p.c. to A.D.P. in the present determinations is about 1: 2; taking the p.e. in its literal interpretation this would mean that, by and large, we could measure such differences as these with a chance of but 1 in 16 that any single consecutive order was incorrect.
It will be observed that the p.e.'s obtained in the study by Cattell are somewhat larger than those here presented. One cause appears at first glance, the twenty judgments of the authors as against the ten of the men of science. But the p.e.'s of ten random selections are also smaller as is also the m.v. Only the first ten Astronomers, Anthropologists, Physiologists and Psychologists have p.e.'s that approach in smallness those of the literary men. This cannot be wholly ascribed to the limitations of position in the lower grades. To what extent differences in the selection of the groups can be held to account for the disparity may also be questioned. If we took the whole thousand American men of science as one group we do not know whether the differences in the first ten would be larger or smaller than in the first ten authors. It is true that there are always more writers than men of science, but abler men may be drawn to the sciences and especially would this be the case near the top, though it is improbable that the psychological limit of worthlessness is so low in science as in literature. Opportunity probably counts for less in letters than in science, and the literary writer seems to be a more specialized type. Then too, in the course of classifying the men of science into twelve groups, we might find that the differences at the top of each group were smaller than at the top of the total of the groups. It is hardly possible to say whether the fact that only living men are included should make the differences smaller or larger.
A priori, we should perhaps expect that, with equal differences, the grading would be easier for the scientific than for the literary men on account of the greater objectivity of scientific work, and because the graders were selected with special reference to their knowledge of this work. We might expect individual taste to effect greater variability in the authors. But it is the natural reply that the literary graders were trained in making just this sort of judgments, and that all the training that they received made directly for greater unanimity. This is, of course, a disturbing factor, but its importance could be easily exaggerated. For example, it may be questioned whether the graders had received special training in judging the relative merits of VII and IX or the relative euphoniousness of IV and V, though there is no abnormal disagreement in either case. Previous training
19) doubtless contributed to II's first place in Originality, but it will be noted that the p.e.'s are not necessarily smaller where previous training would naturally be supposed to have made for most unanimity of judgment. In fact there seems to be little reason why these judgments should not be regarded as equally naive with those of the men of science.
To compare the literary with the scientific p.e.'s on the basis of Cattell's Table IV would be a very hazardous task, in view of the admittedly unsettled character of the hypothesis upon which this arrangement is based, i. e., that the range of ability is the same in each science. If the upper ten men of science were graded by judges with proportioned knowledge of their work the first three would hardly havep.e.'s of .0, as it is of course necessary to assign to them here; the remaining p.e.'s would necessarily be much smaller, but it is impracticable even to guess at their relation to the literary p.p.'s.
( 20)
II. QUALITY ANALYSIS.
If our list of literary qualities were entire, and offered a complete analysis of all kinds of literary merit, the sum of the grades of an author's qualities, properly weighted, should give an exact correspondence to his grades in general merit. It is of course impracticable to approach the problem in this way, it being attempted merely to cover the field as well as possible with ten qualities. How well they cover the field of general merit is measured by the degree of their correspondence with the direct grades in general merit. The list may also cover one author's qualities more completely than another's; in this case the former's grades would approximate, the latter's would diverge from the general merit grade. If there had been omitted from the list some important quality in which an author stood well, his grade in general merit would be higher than the sum of his grades in the qualities. If it were one in which he stood poorly, this sum would be unfairly advantageous to him. On account of the fact that the relative difference in the importance of the qualities is so great, and that an inordinately high or low grade in certain qualities may fall to a poor or good author, the median is a better measure -in this case than the average, because it tends to automatically weight the significance of the qualities. As before, there is no essential difference between the two, but the median should give in general a fairer representation of the truth (see General Table, cols. M. of M. and Av. of Av.).
With two exceptions to the median and three to the average order the correspondence is complete. III receives a much lower grade, IV a slightly lower grade in the median of their qualities than should be the case. A very satisfactory analysis of the other authors is afforded, but the omission of certain qualities has done III and IV an injustice. In the case of III this was anticipated in the arrangement of the experiment. The intellectual appeal plays but a minor part in the list of qualities, and it is precisely here that III is generally supposed to be supreme. It is probable that the lesser displacement of IV is also due to this cause. The list could perhaps be improved by substituting for one of the qualities something that would cover the intellectual appeal. In view of the results obtained, the number of qualities ought hardly to be increased. Ten seems to cover the situation as completely as is necessary. Whether this would be the case in more complicated work, as with human character and temperament, is not determined. The published character analysis blanks generally contain a much larger number than this. Personally, I am inclined to think that ten would suffice. For practical purposes
( 21) this problem would not be quite so complex. We should rather wish to know a person's standing in a certain quality for itself, irrespective of its relation to the general complex of character.
It is possible by various devices to measure the degree of correspondence between the judgments in general merit and those in the qualities. Some qualities are found to depart almost twice as much as others from the general determinations. In an entirely empirical sense, this degree of correspondence may be interpreted as furnishing a measure of the relative importance of any of the given qualities in determining the author's position in general merit. From the present data it would probably be unjust to infer that any of the qualities named was an active disadvantage to an author, or that there were likely to be any striking correlations between the different qualities themselves.
While the results of the determinations appear applicable to this particular group of authors, their value as general measures of relative importance would depend on the supposition that the ranges in the various qualities were somewhere near the same. There is perhaps no particular reason why they should be the same, and to a certain extent differences would be indicated in the positions and p.e.'s themselves. For example, Charm might not be a particularly important trait, yet it might be so absolutely preeminent in an author that it raised his general position higher than it should. The differences in the ranges as indicated by the figures given do not, however, seem to be such as to render the calculations less worth while. And such confidence in their validity as might be derived from further analysis of the results themselves, one of the methods at least does not fail to give.
There is a possibility of one rather disturbing constant error in measures of this nature, whose extent it is never possible to know accurately. There is noted introspectively a tendency to grade for general merit at the same time as for the qualities, and to allow an individual's general position to influence his position in the qualities. This would be the case especially in the case of those qualities that were ill-defined in the minds of the subjects, and tended to be interpreted rather in terms of general merit. We might thus have a grading of Charm by general merit instead of general merit by Charm. This would make the correspondences of such qualities appear closer than they were. It probably does not play any serious part save perhaps with Proportion. It may also contribute to the high position of Finish, but it is difficult to see how it could have been avoided.
The results of the calculations by the various methods to be described are given in the accompanying table:
( 22)
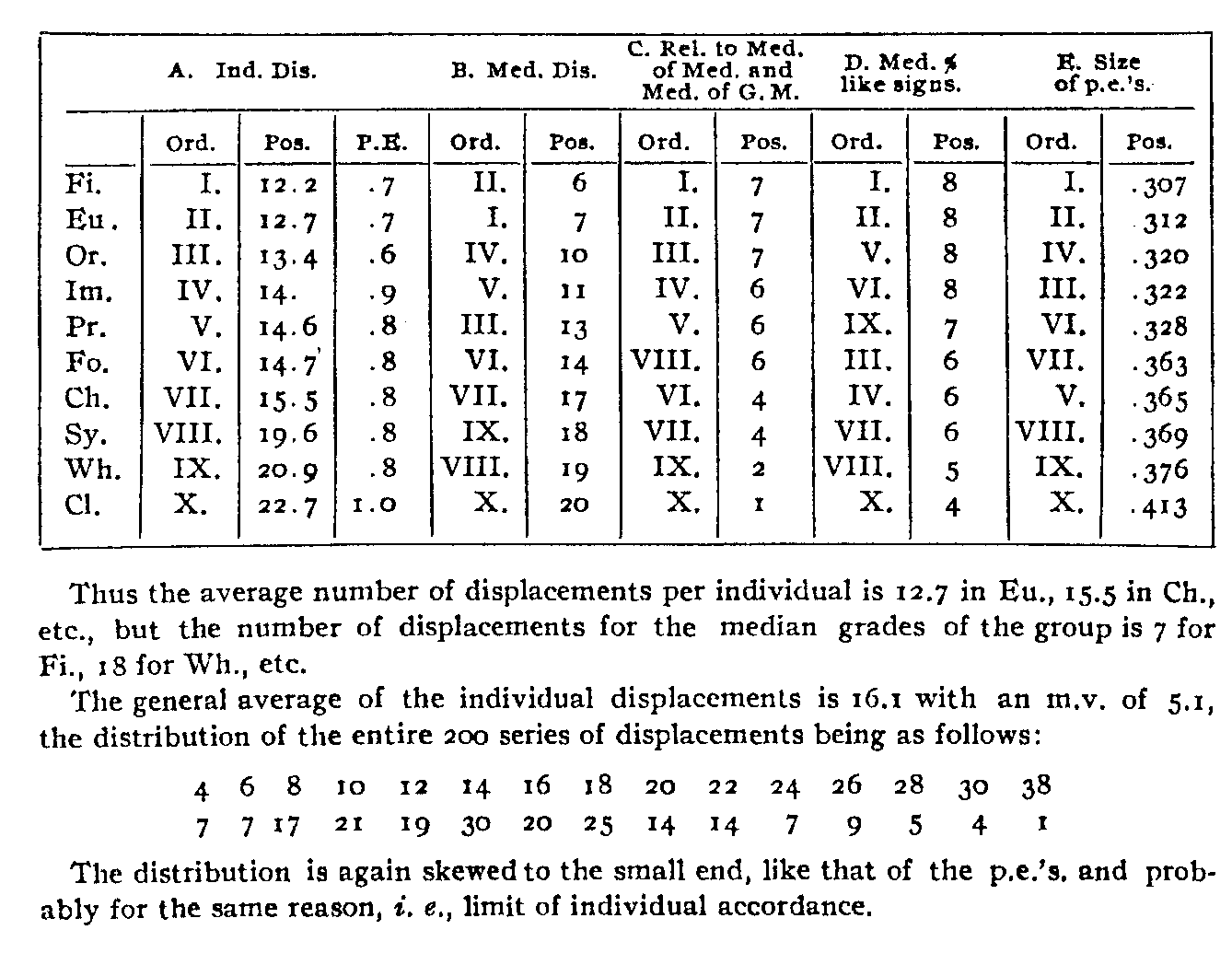
A rough determination of the standards by which our 20 graders judged as a group may be rapidly arrived at by simply making a table in which a + sign is attached to every case in which the quality grade of an author is on the same side of the median of the grades in that quality as the author's grade is on the side of the median of general merit. A — sign means that the quality grade and the grade in general merit are on different sides of their respective medians. Thus I in general merit is also high in Charm, and for this quality receives a + sign. But he is low in Wholesomeness, and in this receives a — sign. Then the quality in which the greatest number of + signs is found is that quality in which an author oftenest stands in a position analogous to his place in general merit. As will be seen, high and low positions in general merit have usually gone with high and low positions in Euphony, Finish, and Imagination, but only once has this been the case in Clearness (Table, col. C).
Correlations by % of like signs were applied, but the results were very inferior to those obtained by the other methods, as shown in column D. It shows just enough agreement to demonstrate its inexactness. While well adapted for certain sorts of work and the only method for cursory observation of individual relationships, it does not seem to operate satisfactorily in the correlation of orders.
It would be difficult, however, to find a correlation method more
( 23) admirably adapted to all relative position work than the measure of displacements devised by Professor Woodworth. In any order of 10 positions, such as we have here, to produce an exactly reverse order (i. e.) correlation -100%Pearson) would require 45 displacements. X being above 9 that he should be below gives 9 displacements, IX above 8 that he should be below gives 8, etc., total 45. Orders that had no reference to the standard would center about 22 and 23 displacements, while the fewer the displacements the higher the positive correlation. For comparative purposes the displacements may be expressed in percentile relation.
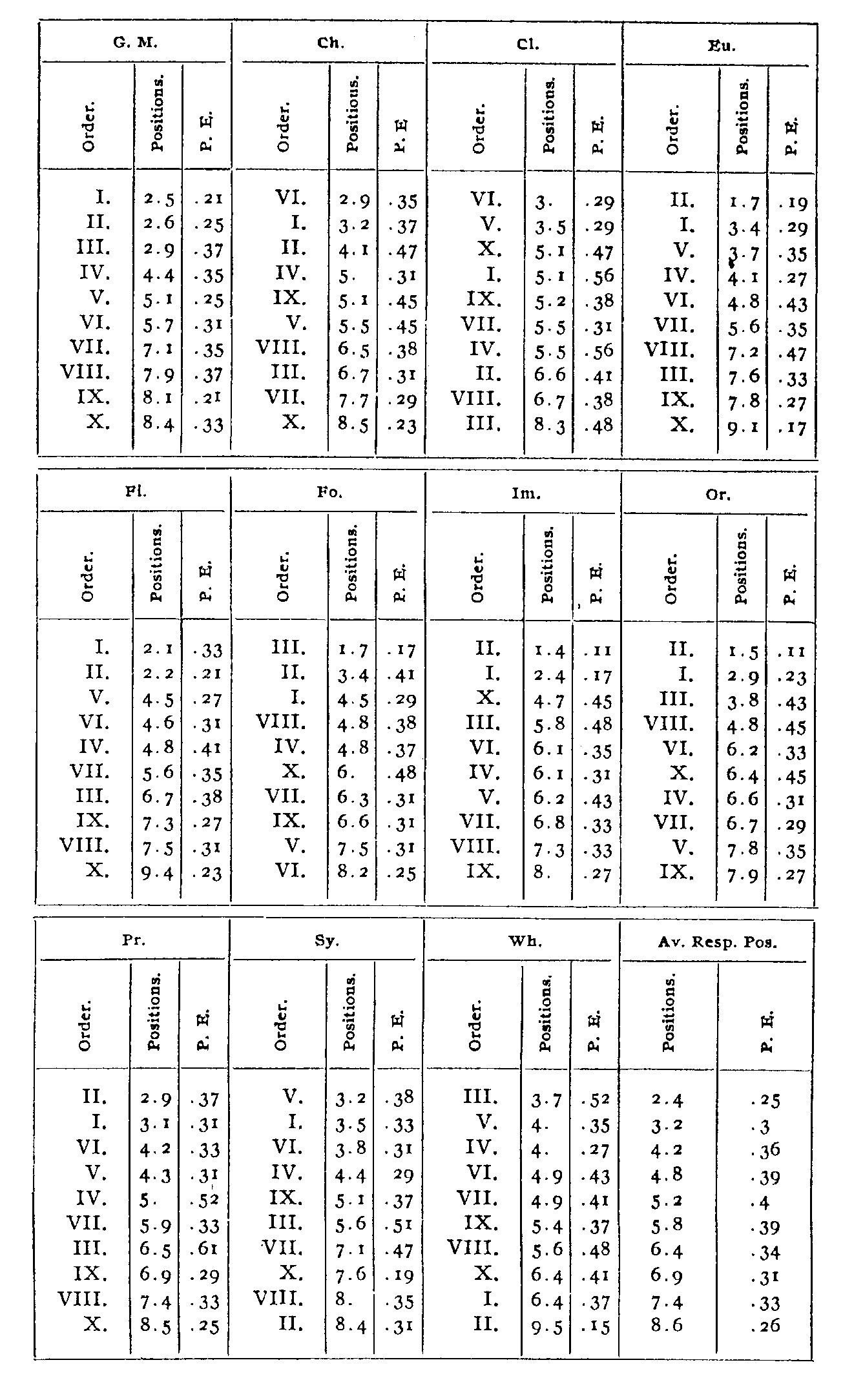
There have been determined by this method the number of displacements from the order of general merit given by the order in each of the qualities (see Table, col. B). This is a rapid means of reaching a generally reliable conclusion, and is much more exact than that afforded by the relation of the individual positions to the general median. It is as yet impracticable, however, to assign a workable p.c. in such determinations and for this purpose I undertook the calculation of the displacements of each quality as given by each individual grader from the order of general merit as given by that individual. The order of correspondence thus obtained has been taken as the standard(col. A), as it seems to possess a measurable and not inconsiderable degree of validity. According to the graphic representation the positions and p.e.'s are as follows:
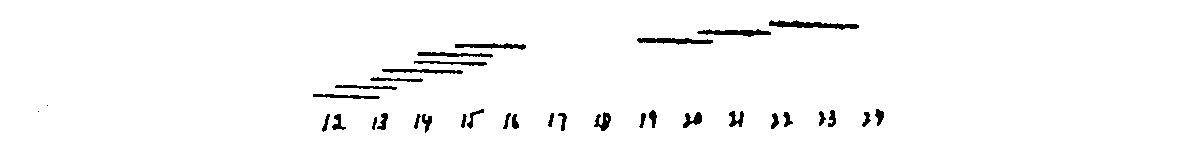
The p.e.'s of the average displacements are larger, yet the differences are usually distinct within two places. The steps are about equal for the first seven qualities, and then we find a considerable gap to the last three, whose p.e.'s are larger, as those at the top are smaller. Some traces of this gap are discernible in the results by the cruder methods. Indeed not the least reason for confidence in these orders is the correspondence they maintain. The B and C orders are practically the same while the very coarsely determined D order keeps well on the positive side. The sum of these orders is practically that given by the standard.
The above orders are all measures of the same general thing, between which, provided they were valid in principle, a certain correspondence would be mathematically necessary. A still closer correspondence, however, is. found with an order mathematically by no means so well associated with the degree of correspondence, namely, the size of the p.e.'s discussed on p. 16, and whose table is reproduced in col. E. It will be noted that the order of relative importance of
( 24) the qualities corresponds to the order in size of the average p.e. with but three displacements. A certain amount of this must indeed be ascribed to happy chance, for the differences in the p.e.'s are often infinitesimal, and were there actually perfect correspondence the present methods would be far too coarse to detect it surely. So far as the results go, the qualities that we tend to judge an author by are also those that we tend to grade with the greater accuracy. It is perhaps not unnatural that the traits about which we have the most assurance should also be those that we regard as the most important. The close correspondence of the two may itself be in the nature of an argument for their validity.
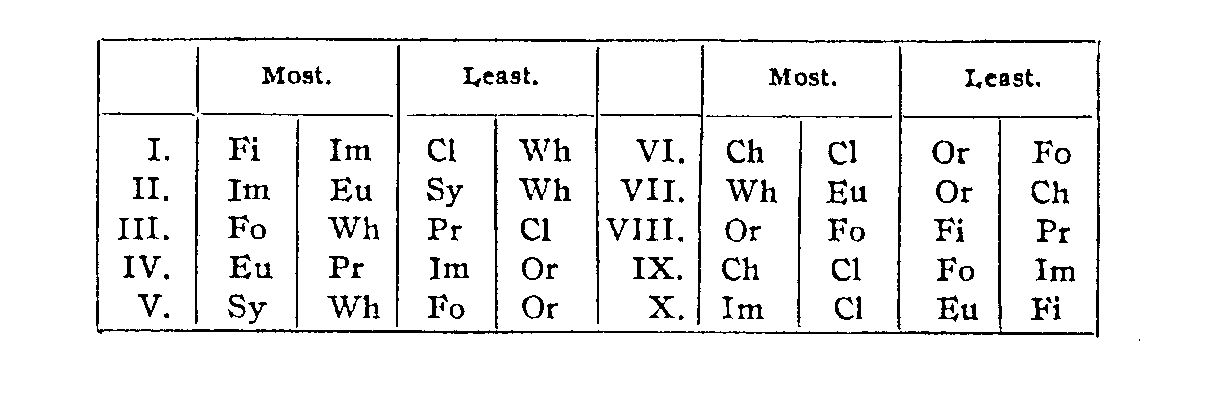
The method measures directly an author's possession of a quality with reference to other authors. Indirectly an idea may be obtained of the prominence or absence of a quality relative to the other qualities of his own work. Aside from such errors as would be due to differences in the ranges, etc., he is likely to have more of a quality in which his position is higher than of one in which his position is lower. Thus I, who has a median of 2.1 in Imagination, but one of 6.9 in Wholesomeness, is probably more imaginative than he is wholesome. A table may be constructed in which a plus sign is given to those quality grades which are at the same time both above the author's median of medians and the general median of the grades in that quality, this last always falling somewhere in the neighborhood of 5.5. Minus is assigned to those grades which fall at the same time below the author's median of medians and the general median of the quality, and a zero sign goes to those which fall between the two. Other things being equal, a + sign then goes to the qualities that are relatively prominent, a — sign to those that are absent, and zero to those which are inconspicuous one way or the other. Such a table contains 35+ signs, 27 — signs, and 38 zero signs. The figure, however, has little significance save when it refers to a prominent quality in a low author or a lacking quality in a high one. The following are in order the two highest and the two lowest quality grades received by each author; i. e., the two qualities for which his work is presumably the most and the least distinguished.
(25)
III. ON THE VALIDITY OF INDIVIDUAL JUDGMENT AS MEASURED BY DEPARTURE FROM AN AVERAGE.
If we took a series of graduated weights, and asked a number of persons to serially arrange them in order of their apparent heaviness, we should find, if the differences between the weights were sufficiently small, that no one could save by chance arrange them in correct order, but that there would always be more or less displacement. The person whose arrangement showed the least displacement would approximate closest to the true order, and we should therefore consider him to have the most accurate judgment for weight. Now assuming that the distribution of all the errors made followed that of the probability curve, we should find that the errors compensated and that the average order in which the weights were placed would also be very close to the correct order, closer probably than that of the best individual, though the average number of displacements might be considerable. In estimating the accuracy of our subjects' judgments of weight, it would make little or no difference whether we took as the true order the actual order of heaviness as measured on the scales, or took the average order as the standard. Theoretically, each would give us the same result.
But there are many important qualities, and indeed those most adaptable to measurement by relative position, whose differences we cannot determine in this objective way. The question then arises, are we also here justified in taking the truth of the average order as objective, and measuring the value of a judgment according to its deviation from it? For clearly unless our average approximates to some objective validity, the absolute value of a single judgment is not measured by the amount of its deviation from it. To recur to our weights, suppose we heated and cooled the weights to varying degrees before presenting them to all save one of our subjects, and to him presented them at equal temperatures. The subjects would all feel the colder weights as heavier, and the average order would not be the objectively true one, and the order of the subject perceiving the weights under equal conditions might well be the farthest from the average. Our two groups would give us different results because they were judging from different standards.
It is just this condition that must be guarded against in those measurements where an average order is all that we have to guide us. We have, a priori, no objective measure of the varying standards by which the individuals judge. Still less do we know the relative values of the standards themselves. In the case of the weights
( 26) we know the differing nature of the standards, and can allow for them; but if we did not know them the judgment of the single subject would still be the most useful for us. Practise will overcome many illusory standards of judgment to which normal persons are subject, and I should hardly have the right to assert my judgment of direction to be superior to that of Professor Judd because I was nearer the average than he in amount of subjection to the Zöllner illusion.
In the measurement of mental traits by relative position we have thus two factors that tend to cause individual deviation from the average, namely the absolute inaccuracy of the judgment, the direction of whose errors will be variable, and a differing standard from other members of the group, the direction of whose errors will be constant, at least throughout the individual. We must know the exact nature of the deviations due to these two causes before we can estimate the values of the judgments. We must also know the value of the standards, for it is possible that the opinion of a very accurate judge by one set of standards might be of smaller value than that of" a less accurate judge by another. We must show cause why a person who judges literary work by its clearness must have ipso facto a poorer judgment than one who judges it by its imagination.
It is possible that in the estimation of scientific merit, where this method found its first application, there would be more unanimity in the standards of judgment, yet there are some divergences: from this cause, since there was an observed tendency for graders, to give disproportionately high position to men engaged in the same special work with them and to their own immediate colleagues. The method has here been applied only to the first fifty psychologists, but it gave fairly definite results, and these might be still more definite in others of the sciences. Save for observer A the order is rather variable, and it might be questioned whether a man's estimate of the fifth group should be allowed the 'same weight with his estimate of the first. This is also a matter subject to a good deal of variation, for the second best judge of the first ten psychologists is the worst of the second, the fifth of the third, the eighth of the fourth, and the sixth of the fifth.
However, where the variations in the standards compensate, as they ought to do in scientific merit, the method is immeasurably more valid than where they not only patently fail to do so but give a false standard, as in literary merit. The conditions are exactly the same as with the varying sizes and temperatures of the weights. Our group of weight-graders constantly gives a small or cold object an undue weight; the group of scientific graders constantly assigns high position to their immediate colleagues and co-workers; the group of literary graders constantly allows a presumably undue weight to
( 27) Euphony and Finish. The variation in the accordance of the judges is a little over 2 : 1, as was the case in Cattell's psychologists; the accordance of the judgments also tends to follow the normal distribution, though there seems to be a slight skew in favor of the more accordant judgments.
It should not be impossible to get a quantitative demonstration of these differing standards. When we have a series of objects graded in respect to a, general quality, and then in regard to the main elements of that quality, the relative influence of the elements on the general judgment appears in their degree of correspondence to the general quality. Now while the graders showed a certain unanimity in assigning to various elements of literary merit a certain order of influence, it does not follow that the mature judgment of eminent literary critics would give the same order, or that the graders themselves would give it twenty years hence. Still less does it follow that this standard is the best one for us to abide by, or that it is one which the graders themselves would not be among the first to consciously repudiate. If we had the qualities directly graded in order of value to literary merit, we should hardly expect to find Euphony and Finish first, Clearness and Wholesomeness last. Nor do we.
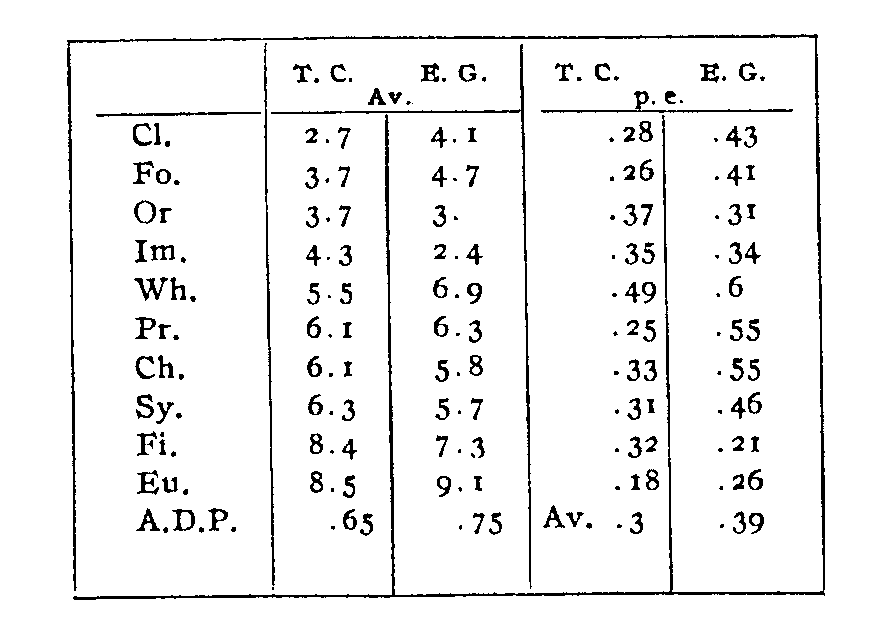
Such a judgment was obtained from a group of 24 graduates in psychology and education, of about the same intellectual level as those who furnished the literary grades. I see no reason a priori—and there is certainly none evident in the results—why the conscious judgment of this group should not have the same ethical value as that of the literary graders, or why the terms should not have been equally well understood. The group contained a certain proportion of women, about one-third, but this factor did not appear to influence the character of the judgments. The formula by which the qualities were graded was "according to their importance to the fulfilment of the highest function of literature." No definitions of any of the qualities were given, nor does it appear that it would have been advantageous to have given them. This order of importance, with positions and p.e.'s, is shown in the accompanying table (cols. T.C.).
This table, compared with that on p. 22, gives an idea of what we think we judge literary merit by as contrasted with what we actually judge it by. The number of displacements between the two orders is 28—slightly more than we should expect by pure chance. Such correspondence as there is between our naive and conscious standards is thus slightly in the direction of perversity. It is probably something more than an amusing coincidence that that quality which we are so sure we ought to judge an author by most of all is the one which really plays the least part in our estimate of him, and that the two qualities which ought to have the least share in deter-
( 28)
-mining an author's position are those which always show the most remarkable correspondence with it.
The distributions of these grades are unimodal for the most part, and only in Wholesomeness do we find distinct species of high and low grades. It has much the largest p.e. and is the only quality receiving a grade in every place. The species were examined for . sex correlations, but none were apparent.
Before the method for the determination of individual standards had been applied, the literary graders had been made aware, through one of the cruder methods, of the general relations of the qualities. It was therefore impossible to obtain from them any order not subject to large constant error. Nevertheless, it seemed worth while to obtain a few records from this group.
Records were obtained from 14 individuals, of whom 12 had taken part in the previous test. The results are given in the last quoted table, cols. E.G. The order and positions here assigned also differ from the objectively determined order by slightly more than the chance number of displacements, but while the number of displacements is almost identical with that of the order given by the other group, there are 11 displacements between the two groups themselves, and in a few cases these discrepancies are outside the limits of the p.e. This may well be due to the constant error mentioned above, and I do not consider that there is sufficient warrant for supposing separate species. An interesting aspect of these results is afforded from the viewpoint of individual comparisons. The number of displacements that occur between the order of the authors in general merit and their order as assigned in the various qualities by a single individual, gives an idea of that individual's actual standards of judgment. The qualities that vary least from the general merit order are his most important standards. In the grading of the qualities themselves we have the conscious standards by which
( 29) the individual thinks he judges. The orders assigned to the qualities naively and consciously are strikingly divergent. The average number of displacements is about 20, a little less than the chance number; it occurs as high as 34, and as low as S. In the former case the individual's conscious standards are almost the reverse of his naïve standards. We might call such a figure a "coefficient of consistency."
The relative smallness of the p.e.'s of the averages assigned by the Teachers' College Group is due wholly to the larger number of graders; the p.e. of the individual judgment, as measured by the m.v., is practically the same in each group. It is interesting to observe that the special training of the literary graders has neither varied the standards to any noteworthy degree, nor given them greater assurance.
There are many complications into which it is not possible to enter deeply. Thus a certain irreducible minimum of Clearness might be most desirable, but once this irreducible minimum were assumed, an analogous degree of Charm might be more important. It must also be remembered that the standards quoted in the table on p. 22 are standards for the criticism of imaginative writers, while the qualities are here graded according to their importance to the fulfilment of the highest function of literature. If we had graded a group of historians, we should probably have found less real judging by Euphony and Finish, and more by Clearness and Force. The standards of judgment for imaginative writing may not be the highest literary standards, perhaps there are other departments of literature which are held to higher standards. But this interpretation is of very doubtful value, since literature, technically considered, is imaginative by definition.
Now the best judge is not the man who judges most true to ordinary standards, but the man who judges most true to the best standards. To discuss what these best standards might be would lead at once into devious ethical pathways; let us call them for the moment the most useful ones. It is probably fair to assume that the maturer, more experienced and distinguished of a group of graders, selected by universal experience for the very abilities which they are here exercising, should, at least in this particular respect, have a better judgment than the remainder of the graders. By this same token, they should also have different standards of judgment, and this would tend to draw them away from the average, but should not, therefore, be held to discount the value of their opinions. After all, the function of a method of this sort is not to tell us what we could not possibly find out in any other way, but rather to determine quickly what in less organized experience might require many years. Its data
( 30) must not run too contrary with those of our every-day experience; even the method of measurement by relative position would itself hardly survive the shock of Aristotle's appearing in the lower half of the world's philosophers. The data of relative critical ability obtained by this method show little accordance with the results of our partially organized experience. It is also true that there is apparent in the results no correlation between accordance of judgment to the average and approximation of individual standards to it; however, when the new factors that would here come into play are considered, it will easily be seen that the present data are much too coarse for such refinements. But the order of critical ability given by the method of direct accordance is quite too far from that of the best experience. Nor does the best judgment for literary merit correspond at all to the best judgment for the various qualities. The worst judge of general literary merit, according to his divergences, is the 3rd best judge of Charm, the best judge of Clearness, and the 13th best of Euphony. The best judge of general merit is the 5th best of Charm, the 14th of Clearness, and the 17th of Euphony.
All that is really given in the individual deviations from the average judgment is the individual who tells us most about the group, or the most accurate judge for a certain set of standards, which, at least in the case of these literary judgments, every one will probably admit to have a rather low ethical value.
We can hardly draw inferences as to the general capacity for sound judgment as measured by the soundness of judgment for any particular class of objects. We must have the information as well as the ability to weight it. It might be that the best judge of the psychologists was he who had the best proportioned knowledge of the work done in the various fields. Judgment may be wholly a matter of information if we make this term synonymous with experience. Obviously then, the fact that one has a good judgment for psychologists tells us very little about the value of his opinion in other fields. To demonstrate the very existence of an abstract power of judgment is ultimately synonymous with the problem of free will. Fortunately it is not in this abstract power of judgment that we need be in the least interested, but rather in the quality of one's judgment for a particular class of objects. We wish to know whether a person is a good judge of distance, of faces, of a mining prospect. To determine this we must pay careful attention to the weighting of the standards of judgment.