The Fundamental Laws of Human Behavior
EIGHTH LECTURE
Max Meyer
Table of Contents | Next | Previous
Substitution of a direct for a devious nervous path. Nervous tension inducing growth. Automatic action. Periodic levels of learning. Two meanings of forgetting. Positive and negative susceptibility of neurons. The curves of learning and forgetting.
THERE is, concerning the fixation of a new path, a very important problem still left. We have reason to believe that in addition to the fixation just mentioned, there is another kind of fixation. Consider this example. When we ask an educated person what six times seven is, the answer is forty-two. When we ask him what six times seventy-seven is, the answer is four hundred and sixty two. Either answer will doubtless be given with the same definiteness and correctness. But there is a great difference in the promptness. While the first answer is enounced directly, the second is enounced only after a considerable delay. The explanation seems obvious. Either path is somehow fixed, but the former, because of the promptness of the response, seems to be much shorter than the latter. As we have just seen, a new path resulting from a variation by deflection is naturally a relatively long path, since the possibility of variation depends on the mediation of centers higher than those of the path to be varied. The fixation of the new path in the manner described does not
(99) change its length and can not, therefore, change the time interval between the stimulation and the response, the so called reaction time. Thus, there must be a second kind of fixation of a path, which implies a shortening of the path. We can explain this by the aid of a comparatively simple hypothesis. This hypothesis must be I he assumption of a property of the nervous system which permits the growth of neurons in places where there were previously none, and thus the shortening of a long path by substituting a direct path for a devious and round-about one. The neurological facts known, point indeed in the direction of such an assumption.
All growth of living tissues, alike in the vegetable and animal world, is of either one or the other kind, by cell division or by growth of the individual cells. Different kinds of tissues, however, show a remarkable difference with respect to these two kinds of growth at the different ages of an animal. In certain tissues, cell division can occur all through life. The necessity of this in certain tissues is clear, for example, in those tissues of which our skin consists. When we have received a considerable wound, involving the loss of some skin, the cells at the edges of the wound divide. The resulting new cells increase in size and divide again; and so on until the opening is completely covered with new skin. Without cell division any new skin could hardly be formed, since there is a limit to the size which individual cells may normally attain. But scarcely any animal goes through life without frequently receiving wounds. In other tissues cell division becomes impossible after the animal has reached a certain age. Since the muscles are of special significance for animal behavior, let us take the muscles as an example. It seems that in human muscles cell division be-comes impossible after the age of from twenty to twenty-
( 100) five years. From this follows the important fact that, in order to become an athlete, a person must exercise his muscles and thus induce both cell division and cell growth before the age of twenty-five years at the latest. If he has failed to do this, the number of muscle cells which he possesses is so small that exercise, because of the limited growth of the individual cells, will now only slightly increase the bulk and therefore the total strength of his muscles. This age limit for cell division differs in tissues of various kinds.
The bulk of the nervous system consists of nervous tissue proper. that is, the conducting tissue, and of supporting tissue. In the latter, cell division may occur at any age. In the nervous tissue proper, however, cell division, that is the multiplication of neurons, stops before man begins his postnatal life. It has been found that about three months before birth man has as many neurons as he will ever have in his life. At this time, however, the vast majority of these neurons are in the undeveloped condition which we have already described. They are little halls without any branches and therefore of little value for the conduction of any excitation. They develop into complete conductors at various times during life. Some develop early, in order to serve those muscular activities which the baby needs immediately on entering into life, for example, the activities of sucking and swallowing. Others develop during the succeeding years of child-hood and youth. It is a peculiar fact, however, that even in old age there are still many undeveloped neurons present. in the human brain. The conclusion offers itself that these undeveloped neurons enable their owner to acquire, even at an advanced age, certain new nervous functions. The numerical possibility that such undeveloped neurons will always, to the time of death, be
( 101) present and ready to take service, appears from the fact that the total number of neurons in the human brain is enormous, uncountable. They have been estimated at from three to four thousand millions. How long would it take us to count so high, if it took but a second to pronounce each successive number? A day of twenty-four hours contains 86,400 seconds, a hundred years only 3153 3/5 million seconds. We could not do the counting in a life time. Thus it does not matter much if we take a few millions of undeveloped neurons with us into the grave, provided that we are thus at any time of our life capable of new adaptations, of new useful habits. Capable also of regaining nervous functions which we have lost in consequence of a lesion within our brain,— say, a bullet having passed through our brain. In such a case, if we arc lucky enough to remain alive, we are found to be incapable of performing certain skilful movements and of reacting in any way to certain stimulations. If a piece of our brain is destroyed, it does not regenerate like a piece of our skin. Its room is filled out with supporting tissue, but the nervous tissue proper, the neurons lost, are lost forever. The functions lost, however, may be entirely or partly regained, just as if they were new habits.
We found it necessary to assume that a new nervous path, a variation by deflection, may first be fixed in its original length and later greatly shortened. We can now explain how this shortening fixation can come about. Suppose a new habit is being formed by the variation of a path, leading now, instead of to the point Mp which corresponds to Sp(Figure 29), by way of a higher center to a non-corresponding point, say Mq. Sp and Mq are supposed to belong to two reflex arches which are very remotely connected, over central sensory and central motor points of a very high order, so that the
( 102) resulting path is of a very round-about and zigzag nature. Figure 29 may been regarded as diagrammatically representing this path, without, however, suggesting that the path in the brain would actually present itself to the eye as a symmetrical figure like this. What is important in the
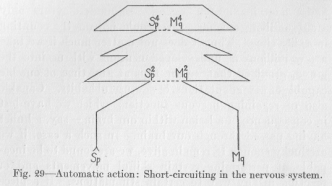
diagram is only that in various places, for example, at Sp, two points of the path are by chance very near each other. Let us assume that in such a case we have between the two points a peculiar, growth inducing, biological condition, just as we should have, if the path were a metallic conductor carrying a high potential current, an electrical tension likely to break through the insulating substance in sparks. This simple hypothesis is sufficient to explain the second kind of fixation of the variation of a nervous path. The biological tension, so to speak, between S4p and M4p causes one or more of the undeveloped nerve cells to grow and send out. branches in either direction of the tension. The consequence of this development of a new connecting neuron is a shortening of the path leading from Sp to Mq, by practically putting out of function the part above S4p M4p , owing to the higher resistance
( 103) of this upper loop. The result of the new growth is that the response at Mq to stimulation of Sp occurs with greater quickness and also with greater definiteness, exclusiveness, for less of the flux from Sp can now reach motor points other than Mq.
The same kind of shortening of the path may occur later between S2p and M2q. Here again the biological tension may cause the development of a new connecting neuron out of an undeveloped nerve cell. The length of the total path leading from Sp to Mq may thus be reduced to almost that of a reflex arch. The response at Mq to a stimulus at Sp must then occur with the same quickness and definiteness as a reflex. That habits can become very much like reflexes is well known. In the drilling of a soldier good examples can be found by any observer. Action of this kind is called automatic. It scarcely differs from reflex action in any respect, save in its origin, which is not hereditary. Its resemblance to reflex action is illustrated also by the resistance which automatic action offers to the destructive influences of certain diseases of the brain. When a nervous disease has made a man's actions entirely illogical, certain automatic actions still occur with the same promptness as most reflexes, for example, oaths--in people who have acquired the habit of swearing in early life. This indicates the probability that our hypothesis agrees with what actually occurs in the brain. Since the disease attacks the higher centres of the brain before the lower centres, the development of automatic action seems to consist in the functional cutting out of higher centres from the path, as explained in the diagram of Figure 29.
If the distance between S2p and M2q had been less than between S4p and M4q, the shortening of the path might immediately have occurred here. This possibility agrees
( 104) with the observation that habitual reactions whose performance at first requires a considerable reaction time, are sometimes made quicker only in numerous stages, some-times become completely automatic almost at one time. Our whole view concerning the shortening of a newly acquired nervous path is thus supported by innumerable experimental studies in the acquisition of skill, for example, in typewriting or in telegraphing. If the growing efficiency of a person learning to write on the machine is represented in a curve, we do not obtain a constantly rising curve, but one which rises to a certain level, remains on this level for some time, rises to a higher level, remains on it for sometime, and so on, as illustrated in Figure 30. Such an im-
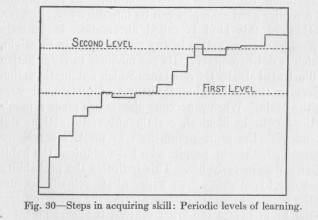
-provement by steps is to be expected if the fixation of the variation of response is not merely a fixation of the new path over higher centers, but at the same time a repeated shortening by cutting off loops from the original winding path. Each time when a loop is cut off, the test of the person's efficiency must reveal a rather sudden improve-
( 105) -ment. After this improvement, however, the efficiency cannot. but remain practically stationary, until another neuron, perfecting its development, cuts off another loop and thus raises the efficiency rather suddenly again to a higher level.
Let us return to what we called the susceptibility of the neurons. On it is based every possibility of a variation of the nervous path, that is, every possibility of learning. We know that the opposite of learning, forgetting, is of as much consequence in actual life as learning. If we call forgetting the opposite of learning, we should do so in only one sense, namely, in so far as a path, instead of becoming fixed, is being obliterated. In another sense the opposite of learning, of a new reaction more useful than the old, is a new reaction less adapted to our needs than the old, as when we "forget" to lock the door in leaving our house. This, obviously, is a case of inhibition, of nervous deflection, rather than of true forgetting. In so far as obliteration is opposed to fixation we are inclined to explain obliteration by a property of the neurons similar, but opposite to that on which fixation is based. We might speak of a negative as well as of a positive susceptibility. We said previously that the susceptibility of nervous conductors consists in their resistance being reduced by a flux occurring in them, and added that the reduced resistance of any nervous conductor very slowly rises again to its original measure. The reduction may be called positive susceptibilty since it is a reaction to function, the rise negative susceptibility since it is a reaction to a lack of function.
In accordance with our statements thus far, the magnitude of the positive susceptibilty must be determined by two factors, the intensity of the nervous process and its duration. In the analogous case the river bed is washed
( 106) out the more, (1) the more water flows through it in a unit of time, and (2) the longer this flow continues. On the other hand, t he negative susceptibility depends only on one factor, the time during which no nervous process occurs in the neuron. It is interesting, therefore, to compare the quantitative results of experimental studies of the progress of learning, which is the effect of the positive susceptibility, with those of the progress of forgetting, which is the effect of the negative susceptibility.
The increasing efficiency of reaction in the process of learning is always represented by a curve like that of Figure 31, rising first rapidly, then more and more slowly,
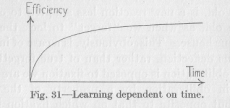
provided that we have in mind one continuous process without any intervening periods of rest. In a longer process of learning spreading over days or months, and containing many extended periods of rest, the efficiency rises, as we have seen, in the manner of Figure 30. We notice that in a continuous process of learning, lasting say, half an hour, the first few minutes are the most valuable. During the following minutes less and less is gained in efficiency, and the last few minutes add so little to the result that we might just as well have stopped earlier. This fact is established beyond doubt by experiment and agrees also with the ordinary experience of any one who has to practice anything, for example, the
( 107) school-boy memorizing a foreign vocabulary. To read over the whole task five minutes a day for a sufficient number of clays to complete it, is much more economical with regard to the total time required, than to complete the task in one continuous memorizing. If we continue the process only for five minutes, we do not make use of the uneconomical part of the time curve farther to the right in the figure. At first glance, the facts represented in this curve seem to overthrow our analogies. Why should a flux, broadening and deepening its channel, do this the longer the less? But the matter becomes clear when we remember that in a neuron, with its limited resources, the flux cannot remain continuously on the same level of intensity. The neuron does not become less and less susceptible to the flux, but the flux becomes in spite of an undiminished intensity of stimulation less and less intensive. The total result, then. must be in accordance with Figure 31.
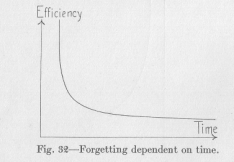
The decreasing efficiency of reaction in forgetting is represented by a curve like that of Figure 3''2. This agrees well with our analogies. We compared the negative susceptibility with the fate of a river bed through which no water flows any more, and which is gradually obliterated
( 108) by being filled with debris and (lust. Such a filling in is usually very pronounced at first., when the banks or the river bed are still steep, less and less considerable later, so that traces of the original depression of the ground may continue for an exceedingly long period. Although the analogy is remote, it shows that the curve may well be expected to have the shape of Figure 32.
This curve, however, of Figure 32 does not indicate what changes, if any, the efficiency undergoes during the time directly following the period of practise, during the first few seconds or minutes, let us say. Now, it is a matter of common experience, that anything we have just learned stays with us, as a rule, for few minutes
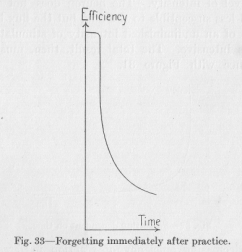
with hardly lessened efficacy and is only then forgotten at a rapid rate. Perhaps the complete curve ought to be drawn as it appears in Figure 33, remaining almost on a level for a short time, then falling very quickly and
( 109) later falling more and more slowly. The usual experiments concerning the rate of forgetting do not tell anything about the first few minutes since they are made only with the intention of recording the loss from day to day. But the ordinary experience is in this case definite and general enough to assume that the loss during the very first few minutes—not to speak of seconds is practically nothing. Let us here record the fact without attempting to explain it.