The Validity of Judgments of Character
Naomi Norsworthy
THE problem of the judgment of character is one which is continually confronting people of all classes and stations. In many instances the correct estimate of a person's character is of vital importance. The success of officers of administration from the President of the United States to the school superintendent of a small village depends often on their ability to choose for their subordinates persons of the proper character. In every-day life one's happy choice of friends, one's ability to sell goods, to persuade people to accept a new point of view or doctrine, to get on harmoniously with people in general in all the various occupations of life depends upon one's ability to estimate the powers, capacities, and characteristics of people. To those who have to make personal recommendations or make use of those made by others, this question of judgment of character is a grave one. Is it possible for one to judge at all fairly the character of another ? When a recommendation is read by an appointing officer, how
( 554) far does he get the estimate of character which the writer intended him to have ? If the question concerned some physical facts about an individual such as his acuity of vision or his height, there would be no difficulty in obtaining a. figure which would express his exact position in this measurement a compared with other people. Even if the question concerned some definite mental trait such as his speed of reaction or perception, or his ability to deal with abstract ideas within a certain field, an exact numerical answer could be given. But with such complex thing as leadership, efficiency, refinement, and the other vague and indefinite traits to which we refer when we use the term character, much doubt may be felt as to whether exact quantitative estimates are possible. This then is the chief problem of this paper. Can such a trait as leadership or refinement be measured in numerical units with any degree of exactitude ? Most people will agree at once that such traits as those mentioned cannot be measured in ordinary units of amount, for, in the first place, the zero points from which to begin the reckoning are not known, and in the second place, these traits manifest themselves in such complicated and subtle ways that the task of expressing them in units of amount is hopeless. Though this method cannot be followed, the method of measurement by relative position in a series might be. People might be ranked in order according to their power of
( 555) leadership or according to their refinement, and if this were proved to be possible, the numerical rating by such a means would be just as exact as though the rating represented units of amount. This method has been used recently by Professor Cattell in his study of the eminence of mon of science.
The traits which I chose for investigation were the following : physical health, mental balance, intellect, emotions, will, quickness, intensity , breadth, energy, judgment, originality, perseverance, reasonableness, clearness, independence, co-operativeness, unselfishness, kindliness, cheerfulness, refinement, integrity. courage, efficiency, and leadership.[1] The question then is: Is it possible to give anyone a rank or position in these characteristics with any degree of exactness?
Individual X, a teacher, was given grade in the above traits by five judges, the mother and the two adult brothers of X, an intimate friend and a colleague in the university, who assigned these grades to X in accordance with the following directions : Give X her position among a hundred college instructors of about the same age in each of the traits mentioned. A rank of 100 in any trait would mean that X stood, in the opinion of that judge, as highest among the Hundred instructors; a grade of 1 would mean that she ranked as
( 556) lowest. Similarly a grade of 80 would mean that of the hundred 19 ranked higher and 79 lower than she ; 34 would mean that 65 ranked higher and 33 lower than she, etc. Two records were taken from each judge, the time between the two varying from six weeks to four months. The gradings were as given in Table I.
The first question to be raised on examining these gradings would probably be, Do they mean anything ? If we had rankings of X by a thousand such judges instead of by five how would the two sets compare ? How closely do these rankings approximate the true ranking of X, meaning by true ranking the ranking given by all the competent people who know X well.
That these rankings mean something and are not the result of random choice or chance is proved in two ways. (1) In the second trials, the same judge does not diverge far from his first rating. (2) The double judgments of the five judges do not diverge far from each other.
To answer this question it is not necessary to use the whole series of traits. The following eight traits have been selected : intellect, quickness, breadth, originality, co-operativeness, refinement, efficiency, and leadership. In the two trials with these traits the overage difference of the first judgment from the second in the ease of A is 9.5. The average difference of the two trials from the aver age of the two (the A. D. dis) is 4.7. A judgment
( 557)
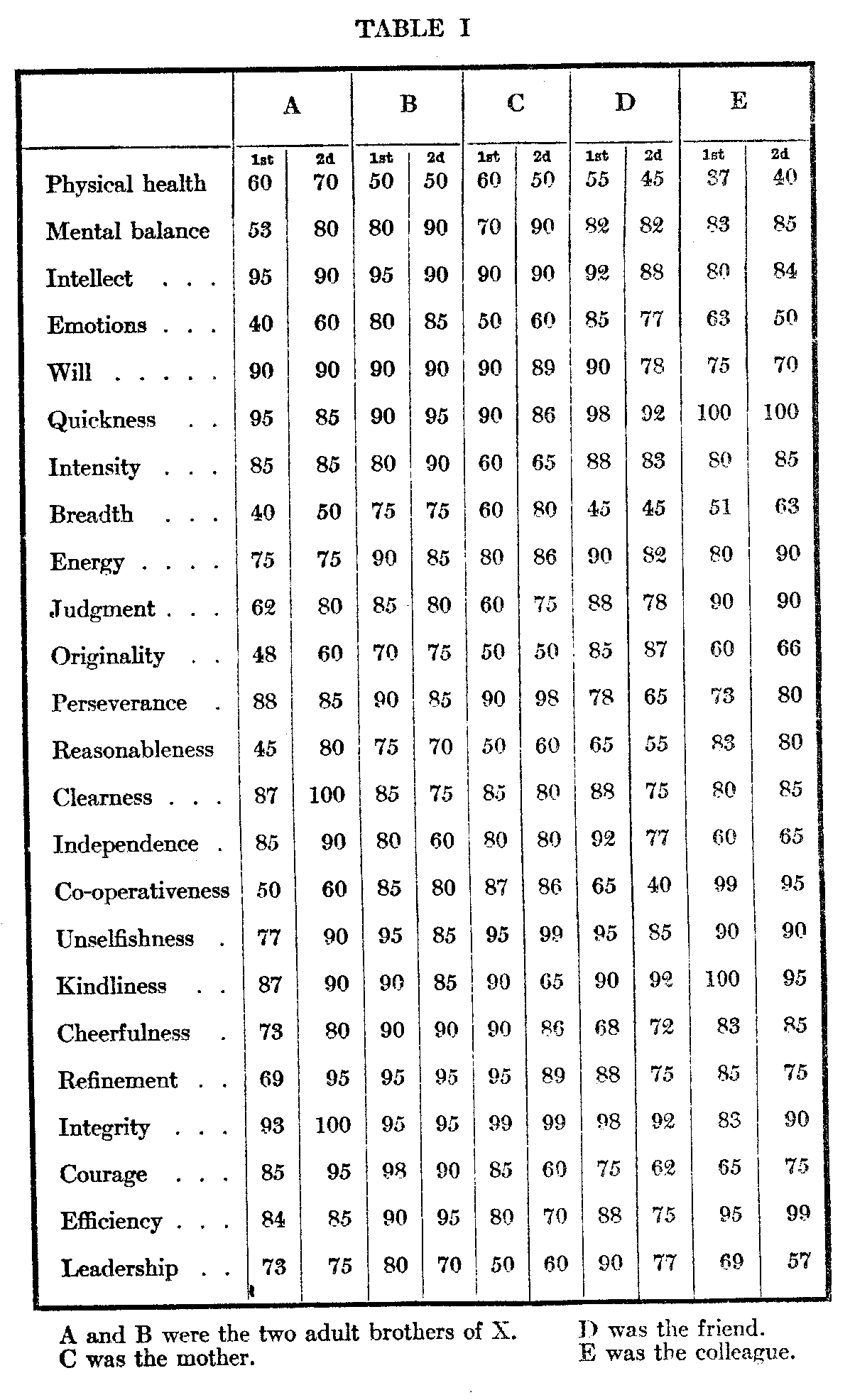
( 558) on the scale of 100 made twice has a reliability of (A. D. dis)/√n or in this case 3.3. This means then that the chances are 99 to 1 against his true judgments differing from 92.5, 90, 45, 54, 55, 82, 84.5, and 74, which are the average judgments of the two trials, by more than 10. Following the same method with the other four judges, the reliability of the average judgment of B is 1.77 ; that of C is 2.12 ; that of I) is 3.33 ; that of E is 2.34 ; the reliability being measured in each case by the probable average divergence of the true judgment from that obtained, by only two trials. Such judges as these then, in two rather casual and hasty ratings of an individual, approximate closely to the results they would give if they rated the individual an infinite number of times. Each judge's measures are at least characteristic of him.
In the second place, the five judges do not diverge far from each other in their estimates of these eight traits, as is shown by the table below.
This means that if we had an infinite number of such judges of X's intellect the chances are about 6 to 4 against their differing from 90 by more than 1.16, and 99 to 1 against their differing from 90 by more than 3.6. These two facts then, first that the individual judges in their second rating do not diverge far from their first, and second, that the five judges in their rating of these traits do not
( 559) diverge far from each, prove that the ratings do stand for some actual quantitative value and are not subject to mere chance. Character then can be measured quantitatively. Such complex traits
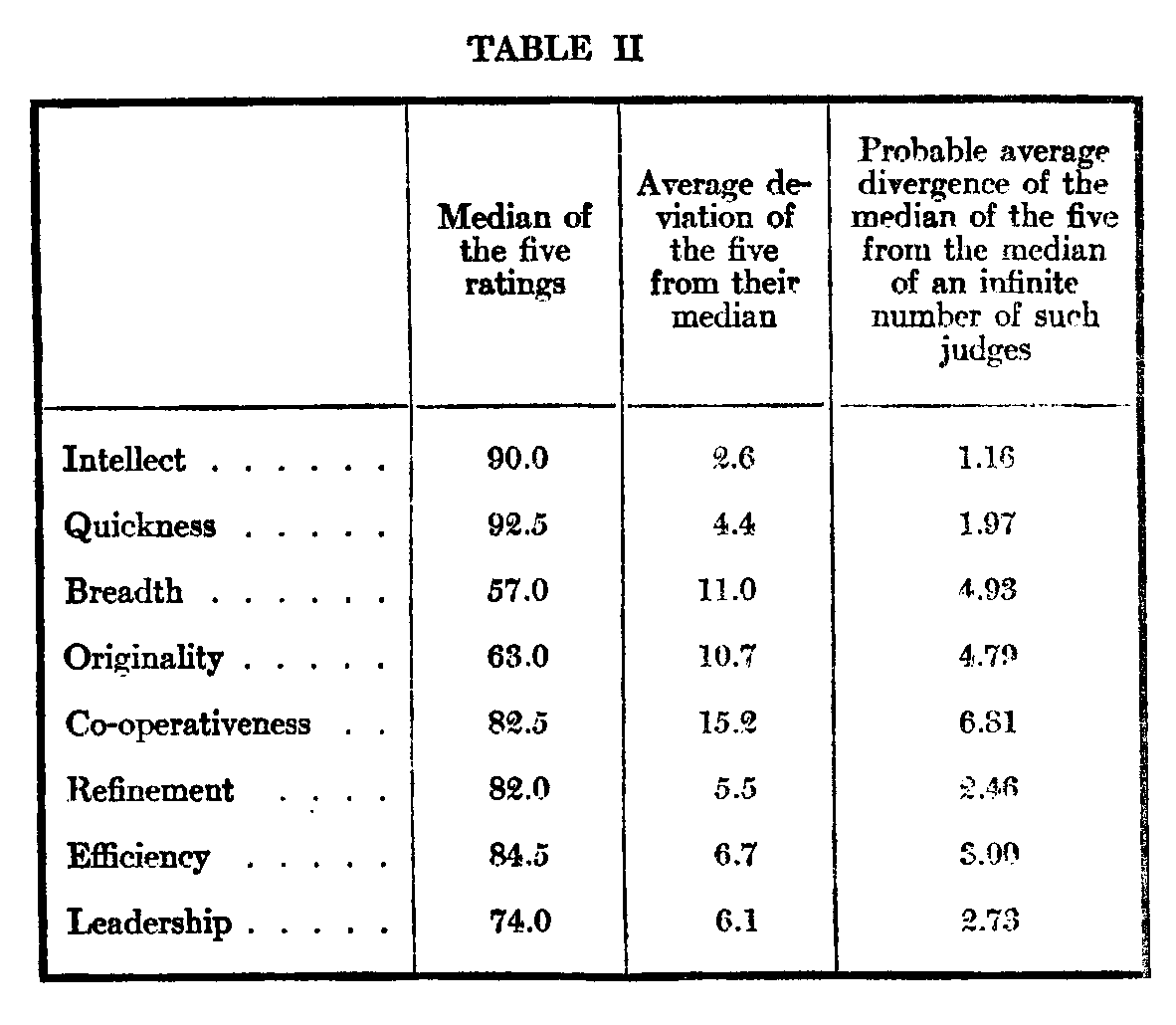
as refinement, leadership, etc., can be rated numerically.
The validity of the judgments in the sense of their correspondence with the actual character of X is then only a matter of the impartiality of the group of judges. If these five judges did as a group represent an impartial judgment of X the ratings of Table II would represent measures of character more valid and more precise than the
( 560) measurement of an individual's discrimination of length or reaction time or memory span obtained from five trials of the kind customarily made.
The certainty of impartiality in the judges can of course never be attained. All the world may be wrong. A working certainty is obtained by selecting judges at random from those who are intellectually competent and are trained in observation of human nature.
These conclusions would be insecure if based on the case of X alone, but they have been fully corroborated by various partial studies of the validity of judgment by other judges of other individuals. For instance, nine members of a college sorority were graded by five of their number with respect to this same list of traits. The different individuals of the nine do not receive the same grades and the different judges do agree to a large extent in their grades of the same individual. That is, the judgments are by no means random ; are reasonably precise ; and are valid in so far as the judges are impartial. The results obtained in the sample case of X may be expected in general.
From such a series of measurements as those in Table II, the question arises, How far is the order of excellence of X in the various traits shown by the table reliable ? The reliability of a difference between two measures equals the square root of the sum of the squares of the reliabilities of the
( 561) measures themselves. The reliabilities of the order ascertained may be seen from Table III.
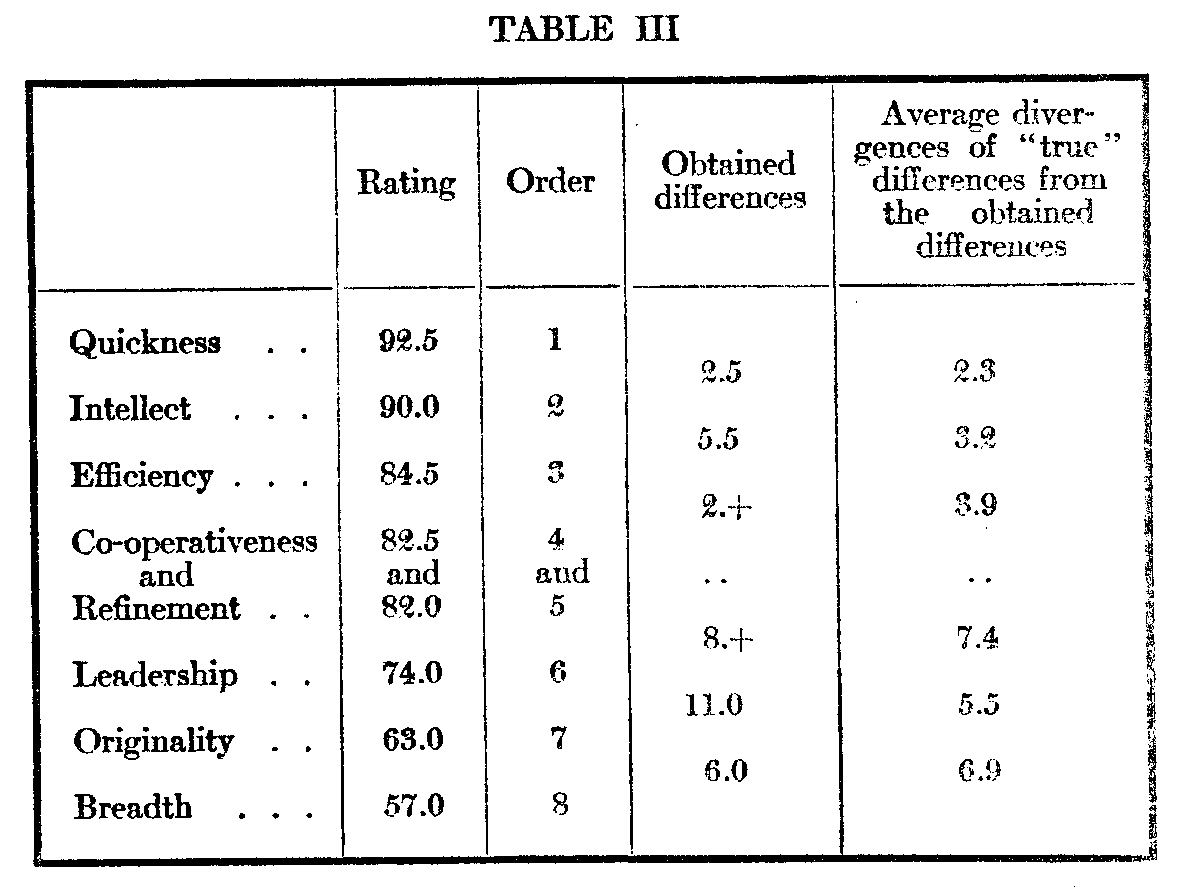
In so far as the judges are as a group impartial in their ratings of X in each of the traits in comparison with their average ratings of X for the whole eight (and that they are approximately so, there can be little doubt), there is certainty (in the score of a probability of 99 to 1) that X is higher in Quickness than in Refinement, Leadership, Originality, and Breadth ; that she is higher in Intellect than in Leadership, Originality, and Breadth ; and so on with other comparisons. The order Quickness-Intellect (1), Efficiency, Co-operativeness, or Refinement (2), Leadership (3), Originality and Breadth (4), is practically certain.
( 562)
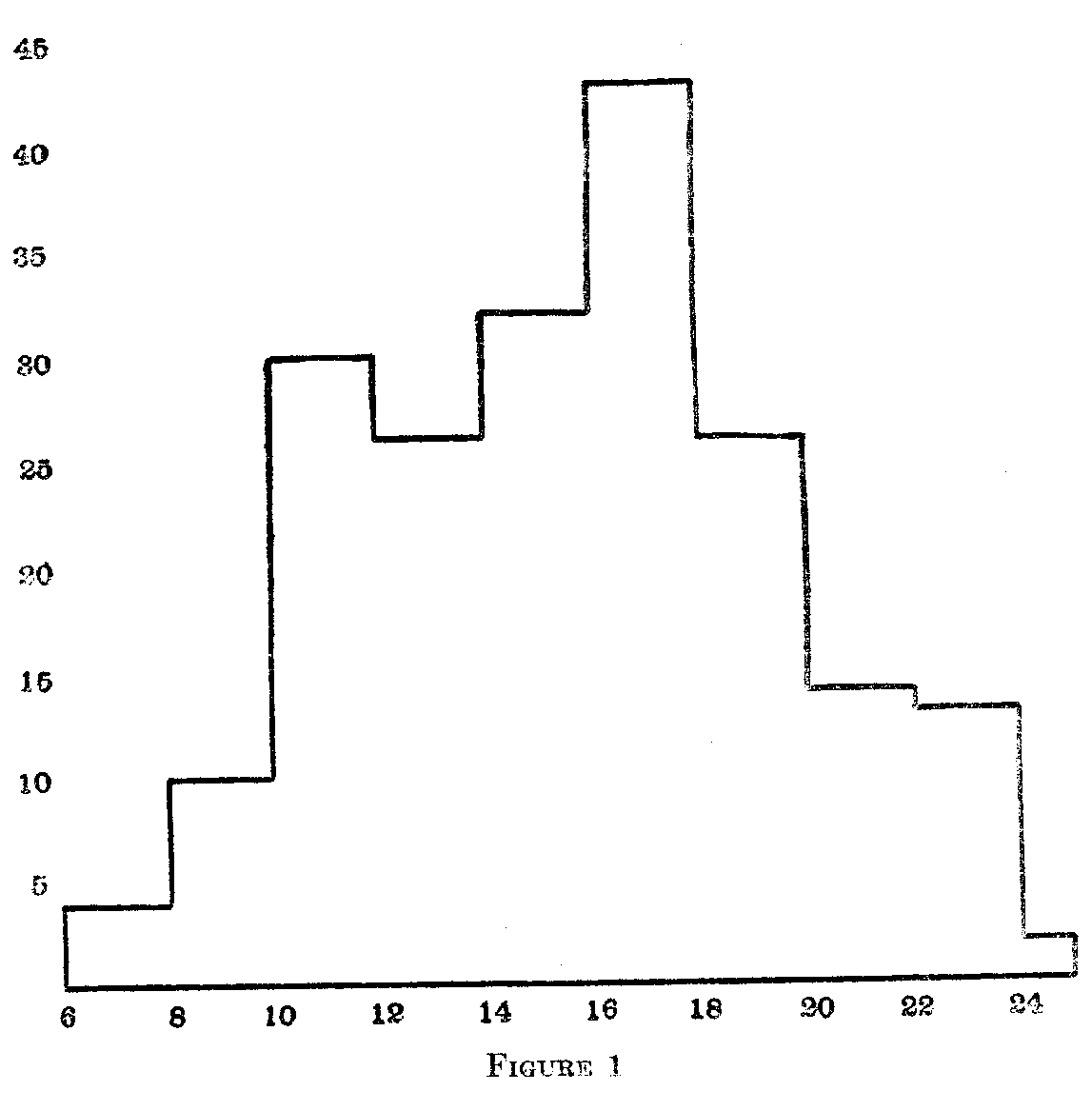
Having then a true estimate of X's rank in these traits. this knowledge might be used to obtain an answer to the question, Is the ability to judge character a measurable power ? It might be possible to rank people in their ability to judge the character of others in the same way that we rank people in their ability to read German, or react to a sound, or sort grays. To test this possibility two college classes were asked to rank X in the traits before mentioned. The directions given were the same as those given to the five judges with the additional request that no names appear on the papers. This was done in order that the judgments be as frank as possible. Three hundred and eighty-seven papers were received, and of these 100 were picked at random. The order of the eight traits determined by the five judges was taken as the standard order. The sum of the variations of each individual's judgment from the true order was found. For instance, one student ranked X as follows : 1 refinement, 2 intellect, 3 co-operativeness. 4 breadth, 5 quickness, 6 leadership, 7 efficiency, 8 originality. The variations of this ranking from the order given by the five judges are 3, 0, 2, 4, 4, 0, 4, 1 and their sum is 18. The 200 students were then distributed according to the sum of errors of displacement from the true order. The total distribution is shown in Fig. l..
This means that there were four students, who in ranking X in the eight traits, made only 6–7
( 563) errors from the standard order. that there were 3'! students who made 14–15 errors from the standard order, etc. It is evident that the sums of the variations from the standard order range from 6 to 24. Probably this does not mean that one
student is four times as good a judge of character as another. The students differed somewhat in amount of knowledge of X as well as in. capacity to judge and the variations due to chance are large. But the data ,do give reason to believe that people differ from each other in this ability as they do in
( 564) mathematical ability or in ability to spell, and that these differences in accuracy of judgment of character can be measured conveniently and precisely by first securing a true standard order of characteristics in say ten persons, who as a group are equally well known to the individuals whose power of judgment we wish to measure, and then proceeding as in the experiment.
This variability in people's power to judge character suggested two further questions: (1) Are there some people about whose character there will be a greater difference of opinion than about others? (22) Are there certain traits about which there is less agreement in judging them than others? To answer the first question it was necessary to have a group of people of about the same age and social standing who knew each other somewhat equally well. A small sorority in a college was decided upon as fulfilling these conditions fairly well. The list of characteristics with the directions as before were given to ten members of this sorority and each was asked to rank every other in all the traits. Three of the girls failed to send papers. The first step in dealing with the seven papers was to ascertain whether the same standard for judgment had been used by each one. To do this the grades of each observer were distributed and her median obtained. It was found that one of the observers had used a very much lower standard than the others, therefore her estimates were
( 565) omitted. The remaining six approximated very closely the same standard — 60 as Med. This left five judgments for each girl in every trait. The Med. and A. D. of the five judgments of each trait for A were obtained. Then the average of the A. D. was found. The same was done for each of the -other subjects. This average for each individual showed the relative variability of the judgments of these sorority members in the case of each other. They are as follows: A, 8.0; B, 7.5; C, 7.5; D, 7.5; E, 6.6; F, 6.5; G, 6.5; H, 6.1; I, 5.7; J, 4.1. From these figures it would seem that among ten girls who know each other well there may he twice as much difference of opinion about some one member of the group as about some other. A, about whom there seems to have been most difference of opinion, was ranked as below the average college girl in seven of the traits. J, about whom there seems to have been most agreement, was ranked at about the average, from 50 to 55 in most of the traits.
The second question, as to the variability in the judgments of certain traits, brought to light some interesting, if not very significant, results. As they were obtained from such a small number of judges, they are only tentative. The papers sent in by the sorority members were used. The aver-age of the A. D. for each trait for all individuals was obtained to show the relative variability of the different traits. The results are as follows :
( 566)

The most noticeable fact about this series is that there is comparatively
little variability — the figures follow each other very closely, there being but
a. difference of between the lowest. and the highest. However, it is interesting
to notice that the traits about which there is most difference of opinion are
Integrity, Kindliness, and Refinement. Evidently people use the words loosely or
their standards for judging these particular traits vary much. more than most of
the others do. From the standpoint of recommendation blanks sent out by
agencies, etc., this is rather unfortunate, for the blanks mentioned always
include matters of integrity and refinement and from these figures it seems
probable that any individual opinion would be less reliable in the ease of these
traits than in the case or any others of the list. Such traits as clearness,
mental balance, judgment, and originality — all of which are important factors
in the success of a teacher — are usually omitted though these
( 567)
are the very traits where the figures show the greatest reliability.
It would seem possible by the use of some such method as this carried out on a very much wider scale, to justify a list of traits, numerical estimates of which by competent people would be both reliable and significant.