Stimulus Dispersions in the Method of Constant Stimuli
Louis L. Thurstone
University of Chicago
The purpose of this paper is (1) to develop a method of numerically evaluating the stimulus dispersions for stimuli that have been experimentally presented by the constant method, (2) to compare two forms of approximation of the law of comparative judgment, namely, Case III which allows for differences in stimulus dispersion among the stimuli, and Case V which assumes that all of the stimulus dispersions are equal, and (3) to describe a criterion by which to decide whether Case III or Case V should be used with a set of data collected by the method of constant stimuli. Since the present study is a continuation of previous work on the law of comparative judgment the concept of stimulus dispersion (1) and the concept of the psychological or experiential continuum will not here be repeated. For the same reason the assumptions underlying the five cases of the law will not be repeated. We are concerned here with the solution of a problem that has been found rather troublesome, namely, the numerical evaluation of the dispersion or ambiguity of each stimulus. Description of the experimental data and the two cases under which they may be treated will be preceded by a short discussion of the logic of the problem.
Psychophysics is the quantitative study of the discriminatory process. In such a study we deal with two principal continua, namely, the physical stimulus increments and the apparent or experienced increments. These two continua are designated the R-scale for stimulus increments and the S-scale for the apparent or experienced increments. Fechner's law expresses the logarithmic relation between these two variables in the form S = k log R in which k is a constant and in which the experienced increments are measured from the experience of unit stimulus as an origin.
( 285)
A psychophysical problem may be stated in two essentially different ways. First, it may be the problem of describing the discriminatory process in terms of the physically measured stimuli or, second, it may be the reverse, namely, to describe the stimuli in terms of the discriminatory process. Both of these types of psychophysical problem employ the same experimental methods and the same logic. Of these two types of problem the first is much the more common in psychophysics but it is probable that the second type of psychophysical problem is much the more important for psychology. Limen determinations belong to the first type in which one aspect of the discriminatory process is described in terms of a stimulus measurement. The limen is a stimulus measurement which is used to describe the discriminatory process. It will be readily seen that this first type of psychophysical problem is much the more restricted because it can be stated only for those stimuli which can be rather unambiguously measured, physically, in the attribute by which they are discriminated. No such limitation exists for the second type of psychophysical problem in which we pivot on the discriminatory process so that stimuli and their differences are described in terms of the discriminatory process. Thus, for example, the similarity or difference between two stimuli A and B may be described in terms of the ease with which they are differentiated even though neither stimulus can be physically measured in the attribute by which the subject differentiates between them. Of course, the same problem can also be stated for those stimuli that can be so physically measured but physical measurement of the stimuli is in no sense a prerequisite for the description of their degree of similarity in terms of the ease with which they are actually differentiated.
Suppose that a series of brightnesses are to be studied by the two formulations here described. According to the first we should determine, experimentally, that brightness increment from any one of them as a standard which is correctly discriminated in, let us say, 75 percent of the attempts. That stimulus measurement would be the limen. But with the same data before us we may reverse the question and ask how
( 286) many experiential units there are between two of the brightnesses. That question can be answered without even knowing the photometric values of the brightnesses and without altering the psychophysical experiment.
In both of these forms of the problem we need to have an experiential unit of measurement. It is necessary for the limen determination as well as for our second formulation of the psychophysical problem. The just noticeable difference is regarded as experiential unity but it is of course measured physically. The writer has proposed a truly mental unit of measurement, the discriminal error (2), as a substitute for the just noticeable difference since the discriminal error is by definition an experiential process and as such it is more appropriate for measuring experienced increments than the physical measurement, the j.n.d.
In the method of constant stimuli there are two stimuli presented to the subject for discrimination in a prescribed attribute. If the stimuli can be physically measured it is of course possible to say definitely whether any judgment of the subject is correct or incorrect. The correctness of an experienced difference between the two stimuli is assigned then by pivoting on the physical measurement as relatively in-fallible. If the two stimuli cannot be physically measured in the attribute judged, then the judgment is handled statistically in the same way except that the judgment returned in the majority of the attempts is then called the correct order. This latter criterion of correctness agrees with the first and is applicable to stimuli that can be physically measured as well as to those stimuli that cannot be physically measured in the attribute by which they are discriminated. Hence the latter criterion is the more universal and psycho-logically the more significant.
The principal psychophysical problem is the measurement of the experiential increment between the two stimuli because their physical measurement presents no psychological problem when the attribute that is discriminated can be physically defined. In psychophysical problems of this type it has been assumed that equally often noticed differences are psycho-
( 287) -logically equal. This assumption is known as the Fullerton-Cattell theorem and it is no doubt correct for many simple stimulus series but it is not valid for stimuli that differ in what the writer has defined as stimulus ambiguity (I). By this is meant the dispersion projected by the stimulus on the experiential or psychological continuum that has been de-scribed so that it lends itself to objective experimental treatment.
The law of comparative judgment is the fundamental equation for the method of
constant stimuli. It expresses the experiential increment as a function of the
frequency of similar discrimination, Pa>b, and the two stimulus
ambiguities or dispersions on the experiential continuum, σa and σb.
The law has been discussed under five cases (1), each of which has its own
assumptions and approximations. In the simplest case the stimulus dispersions
are all assumed to be equal and the Fullerton-Cattell theorem is then valid. The
customary stimuli of psychophysical experimentation such as brightnesses, line
lengths, and lifted weights, are obviously so uniform as to stimulus dispersion
or ambiguity that the use-fulness of the equation of comparative judgment is
more clearly demonstrated on stimuli that may be assumed to vary considerably in
stimulus dispersion. Such is the case with the affective values (4) of
nationalities and races in response to the question, "Which would you rather
associate with? "
THE EXPERIMENTAL DATA
A printed schedule of pairs of nationalities and races was submitted to 250 children in the Hyde Park High School in Chicago. The instructions were as follows :
"This is an experimental study of attitudes toward races and nationalities.
You are asked merely to underline the one nationality, or race, of each pair
that you would rather associate with. For example, the first pair is:
ENGLISHMAN—SOUTH AMERICAN
"If, in general, you prefer to associate with Englishmen rather than with South Americans, underline Englishman. If
( 288) you prefer, in general, to associate with South Americans, underline South American. If you find it difficult to decide for any pair, simply underline one of them anyway. If two nationalities are about equally well liked, they will have about the same number of underlinings in all of the papers. Be sure to underline one of each pair even if you have to make a sort of guess."
The schedule contained a list of pairs of nationalities and races so arranged that each of the nationalities listed in Table I was paired with every other nationality and race in the list. Since there are thirteen nationalities in the list there were
n(n — I)/2 = 78 experimentally independent judgments from each subject.
It is entirely irrelevant for the purposes of the present problem whether each of the thirteen social stimuli were nationalities or races or religions in any anthropological sense. It is possible for example to have a prejudice against South Americans without reference to any particular South American country and hence such a category is legitimate for a psycho-physical study even though it might be entirely illegitimate in an anthropological study. We shall refer to the thirteen stimuli as nationalities without repeating this reservation.
In Table I we have a summary of the preferential judg-
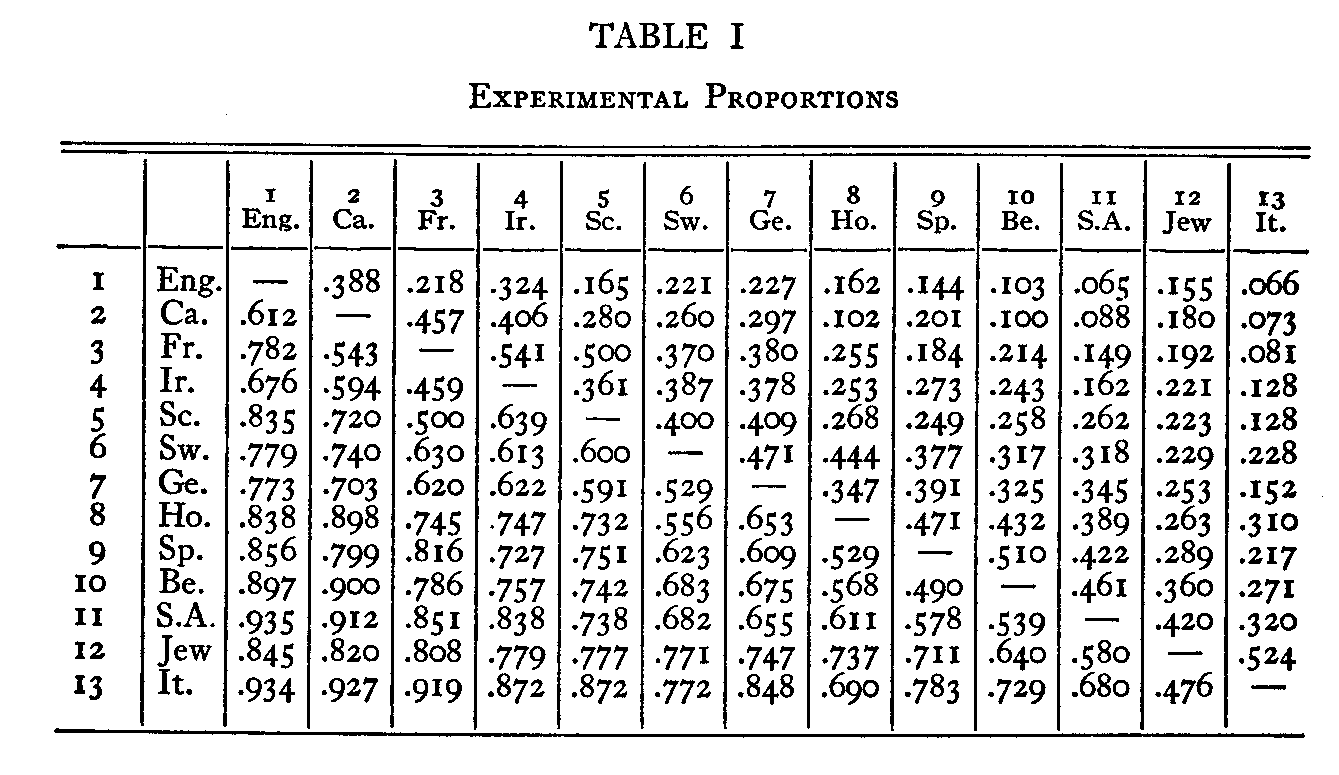
(289) -ments of our subjects. It shows the proportion of the subjects who preferred each nationality at the top of the table to each nationality at the side of the table. For example, the proportion of subjects who preferred Hollanders to Canadians was .102 and, since the intermediate category of judgment was not allowed, the proportion of subjects who preferred Canadians to Hollanders was .898. All of the other entries in Table I are read in the same manner.
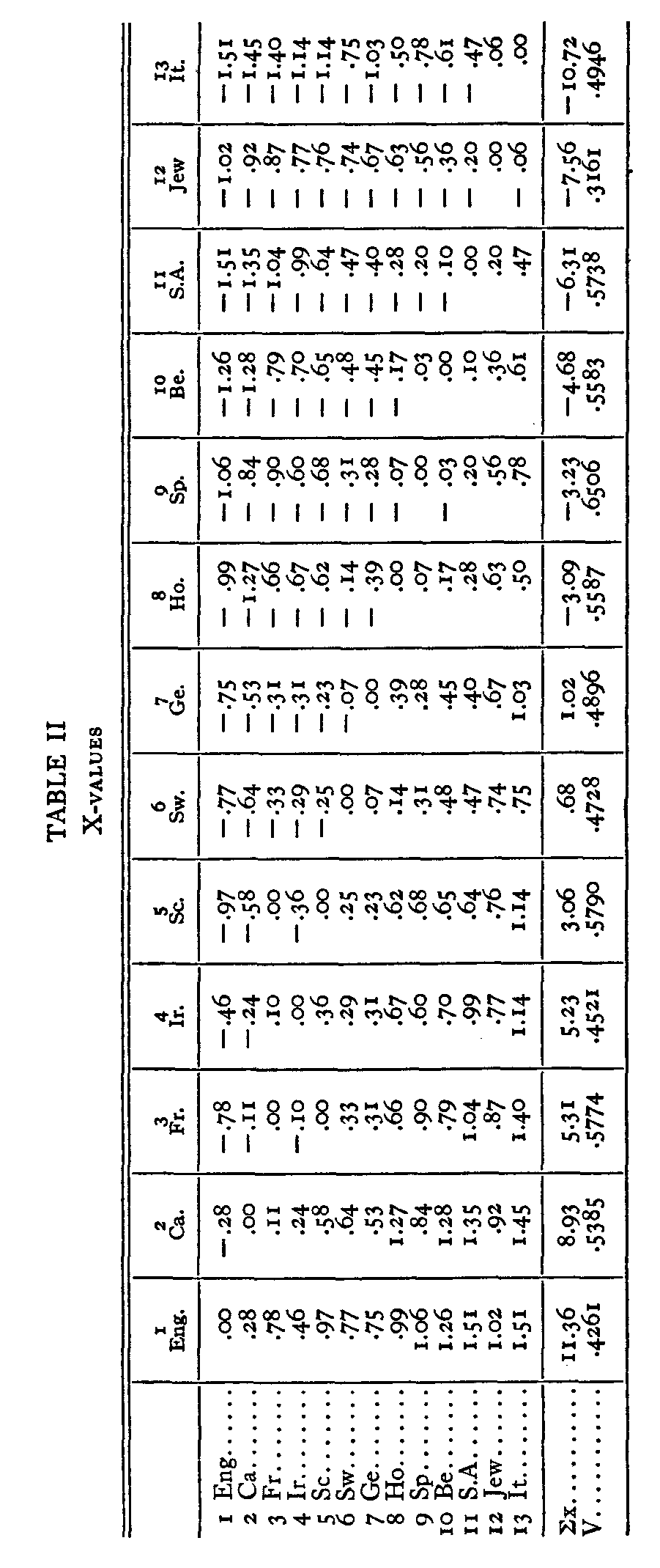
In Table II we have the corresponding x-values which were read directly from the Kelley-Wood tables. Continuing the same example, we enter the Kelley-Wood tables with the proportion .102 and we find the x-value 1.27 which has a negative sign because the proportion .102 is less than .50. When the proportion is greater than .50 the x-value has a positive sign (4). At the foot of each column is the algebraic sum of the x-values, Σx, and the standard deviation, V, of the column of x-values.
The law of comparative judgment in Case III is written in the form (1) :
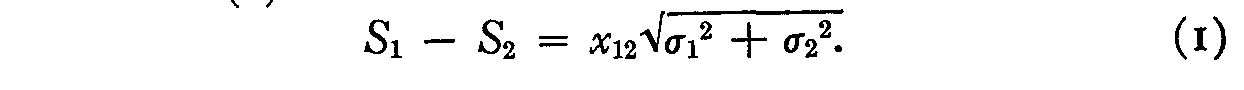
This equation can be written in the linear approximation form:
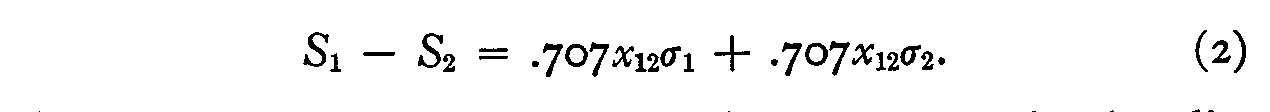
which has been called Case IV. When the two stimulus dispersions in (I) are assumed to be equal to unity the law takes the simplest form, namely,
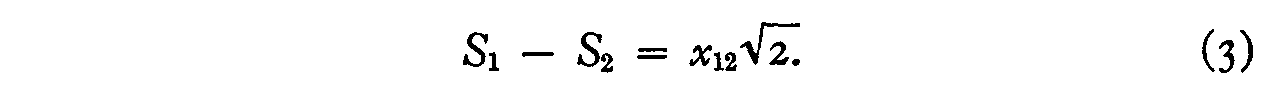
which we have called Case V.
CASE V OF THE LAW OF COMPARATIVE JUDGMENT
The data will be evaluated first by Case V because it is the simplest. Let Sk be the scale value of any one of the thirteen stimuli. We then have
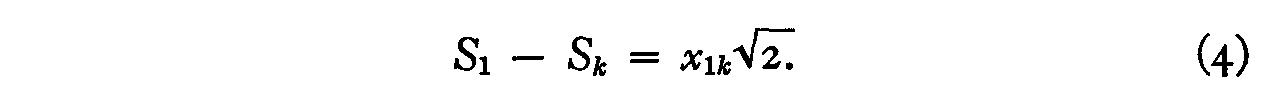
Summing for all thirteen stimuli, we have
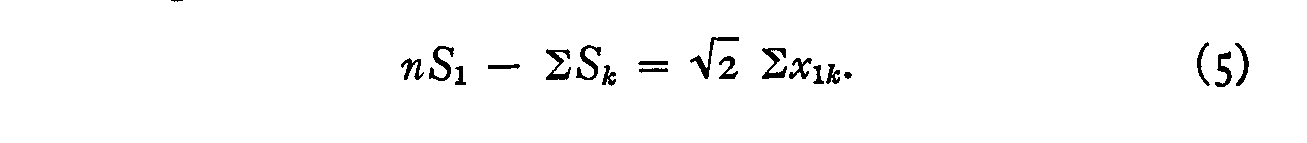
(290)
( 291)
But we may allocate the origin at the mean of all the experiential values so
that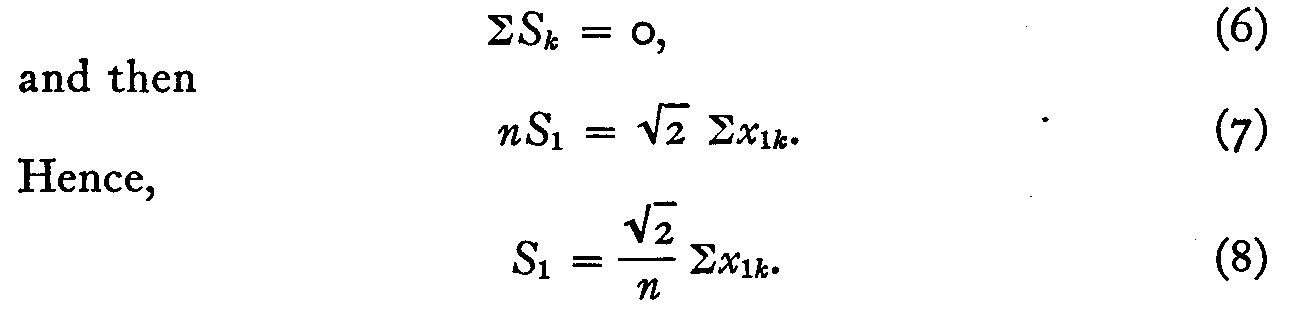
The sum of the first column of x-values is 11.36 and hence the affective or experiential value of the first stimulus is +1.2357. This is the affective value recorded for the English in Table III by Case V. All the other affective values by Case V are computed in the same manner. See Table III. The sum of the affective values in Table III is -0.0001 or practically zero as postulated in equation 6.
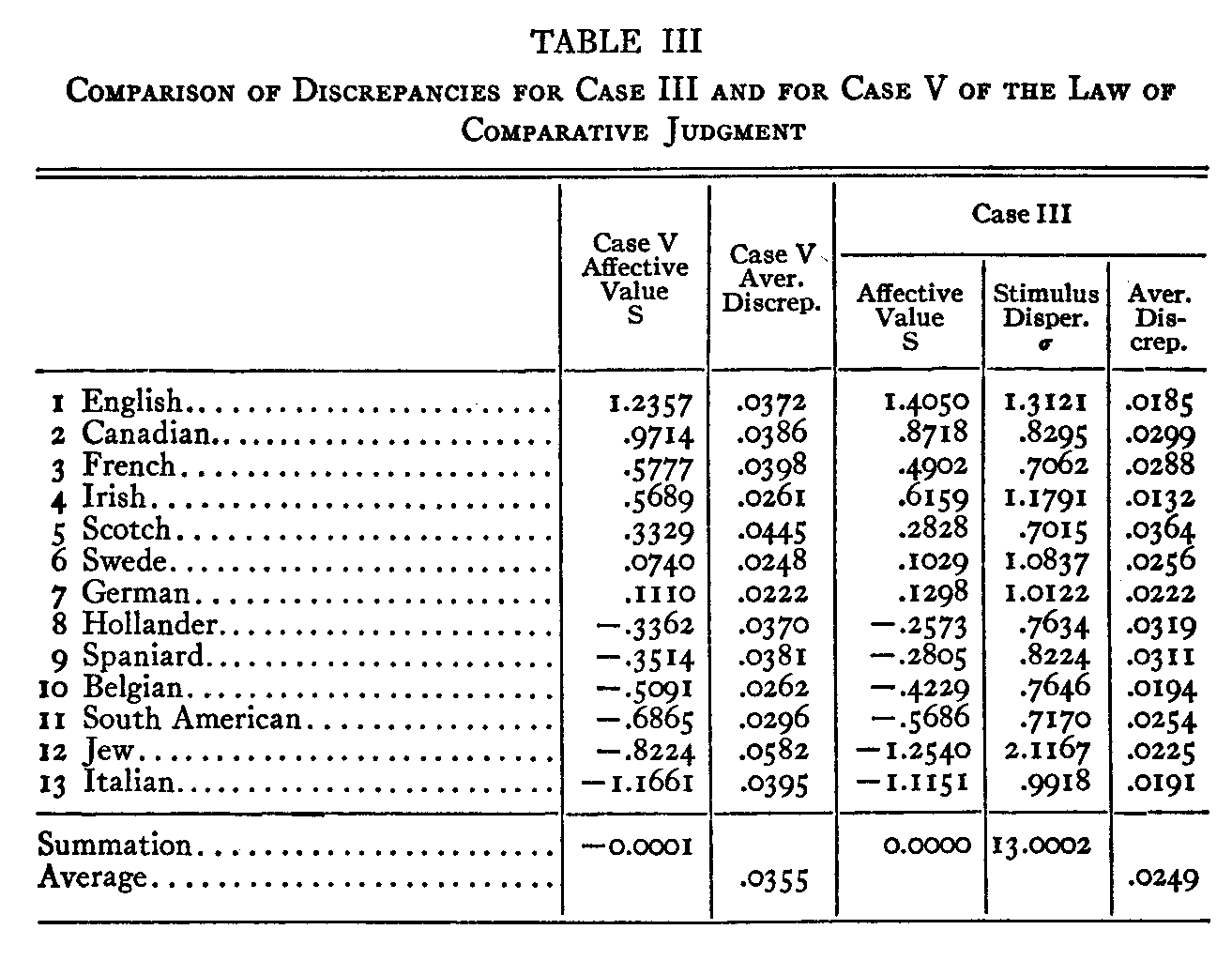
With the thirteen scale values in Table III calculated by Case V, we next ascertain how well these scale values fit the data. The thirteen scale values should lock the 78 experimentally independent proportions on Table I. For example,
(
292) the scale values of the Canadians and the Spaniards are +.9714 and
–.3514 respectively. Their difference is 1.3228 which when substituted in
equation 1 gives an x-value of .935 and this, by the Kelley-Wood tables, gives
an expected proportion of .825 favoring the Canadians when compared with the
Spaniards. The experimentally obtained proportion was .799 which shows a
discrepancy of .026. This is a fairly satisfactory agreement. In order to
ascertain the agreement over the whole table, the 78 discrepancies were
calculated as in the above example. In the fourth column of Table III we have
the average discrepancy between the experimental and the calculated proportions
for Case V. Thus, in Table III the average discrepancy between the twelve
experimental and calculated proportions for the English is .0372, for the
Germans it is smallest, namely, .0222, while for the Jews it is the largest,
namely, .0582. The average discrepancy for the whole table is .0355 which is
here the principal value sought. This value we shall compare with the average
discrepancy for Case III in which the stimulus dispersions are not assumed to be
equal.
CASE III OF THE LAW OF COMPARATIVE JUDGMENT
If we write equation 4 for any two stimuli such as the English, No. 1, and the Canadians, No. 2, we have
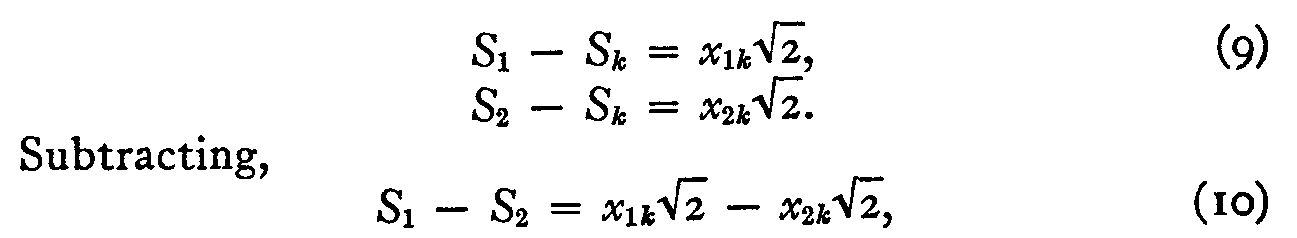
in which (S1— S2) is constant, namely, the difference between the two scale values for the English and the Canadians, irrespective of the nationalities that are successively represented by the notation k. Equation 10 may be rewritten in the form,
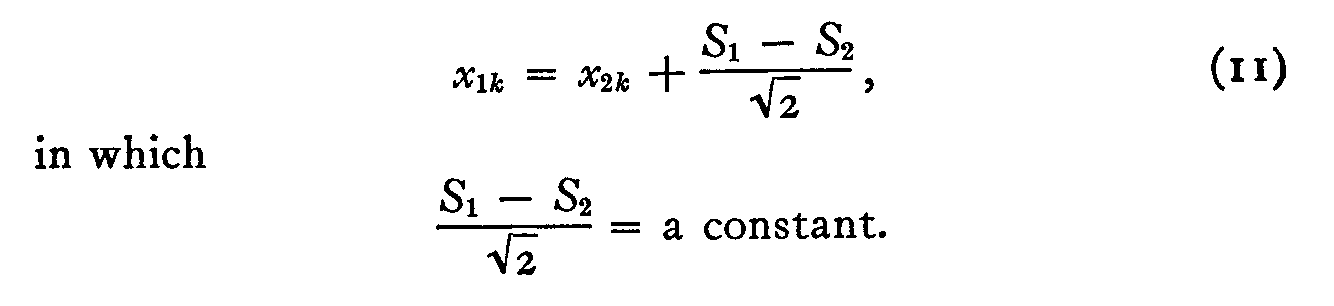
(293)
Now, this is evidently the equation of a straight line with a slope of unity. It may be tested by plotting experimental values of x1k against x2k and similar tests may be made for any other pair of columns in Table II. When that is done it is seen that the best fitting straight lines do not have a slope of unity and the author suspects the reason to be largely in the differences of stimulus dispersion among the thirteen stimuli. For this reason we may try Case III which does not make the assumption that the dispersions are all equal.
We may write the law of comparative judgment for two stimuli I and k in the form:
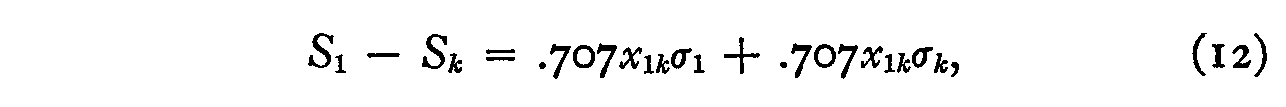
and, similarly, for the stimuli 2 and k:
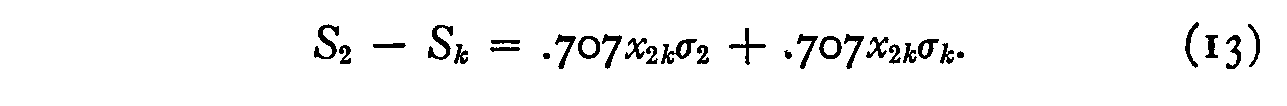
Subtracting, we have
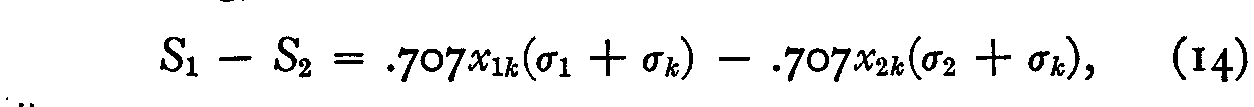
or
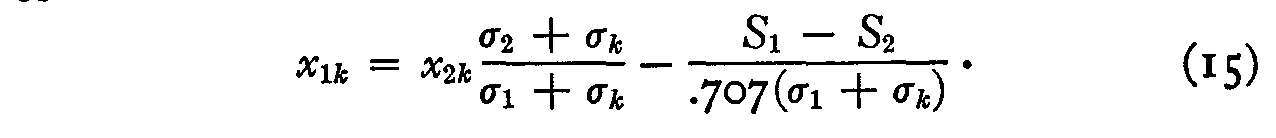
If x1k be plotted against x2k this plot should be linear with a scatter that is due to (1) chance errors in original proportions and (2) the ignoring of variations in σk which may be assumed equal to unity in the linear regression or approximation equation:
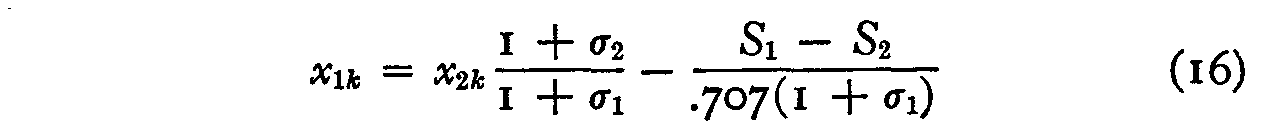
It should be noted that σl and σ2 are not assumed to be equal. The slope of this linear plot should be
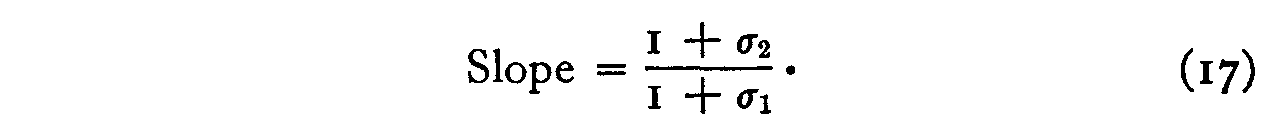
But the slope can also be determined from the ratio of the dispersion of the values of xlk and the dispersion of the value of x2k.
Let VI= standard deviation of values of x1k and
V2= standard deviation of values of x2k
( 294) Then
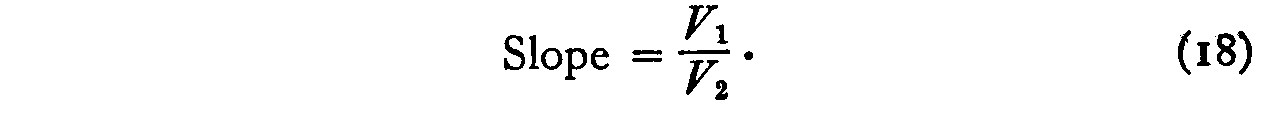
But equations 17 and 18 are two measures of the same slope. Hence, approximately,
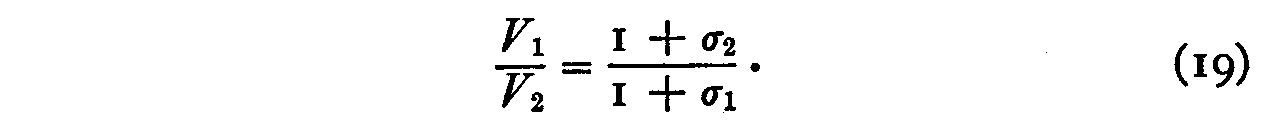
In other words, the dispersion of the values of xlk is inversely proportional to (1 + σl) and similarly for each of the other stimuli, so that
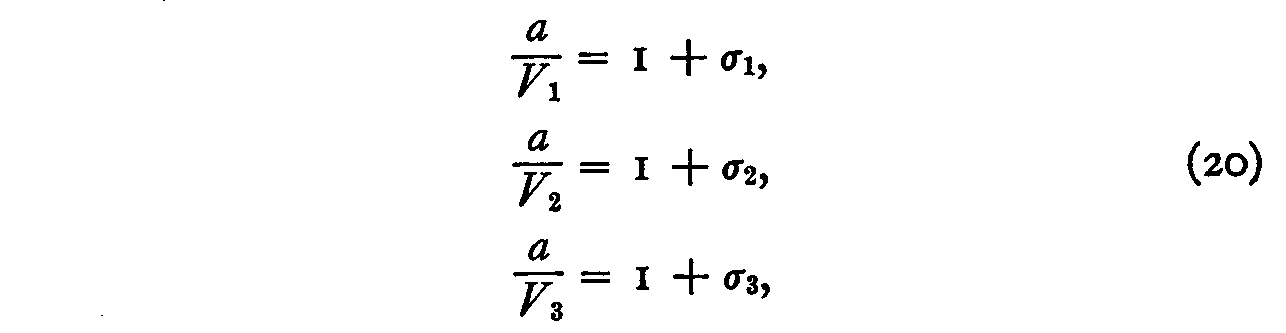
and so on, in which a is a constant. If we sum these n equations (20) we have
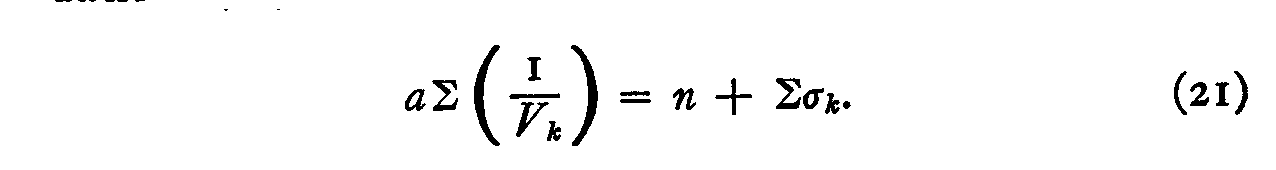
But we may define our unit of measurement as the average stimulus dispersion so that
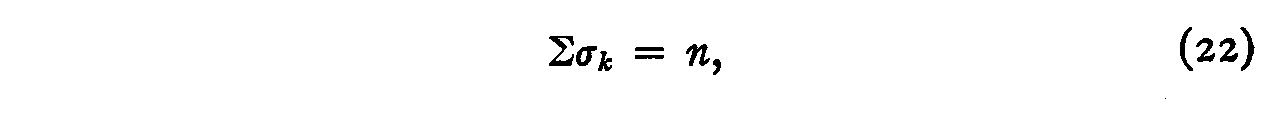
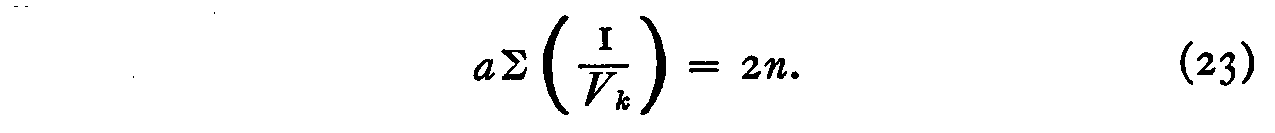
The value of the constant a may be readily determined from equation 23 as
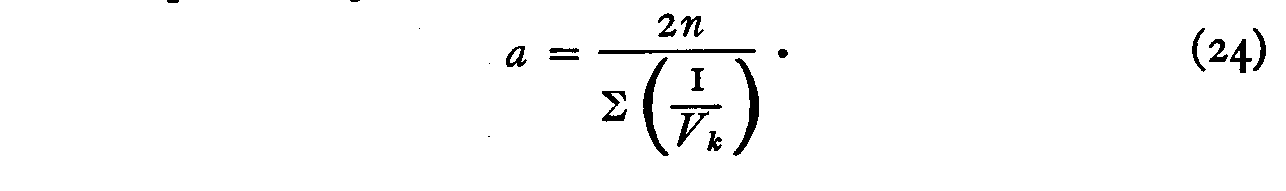
With the constant σ known we calculate each of the n stimulus dispersions from the following equations, obtained directly from equation 20,
( 295)
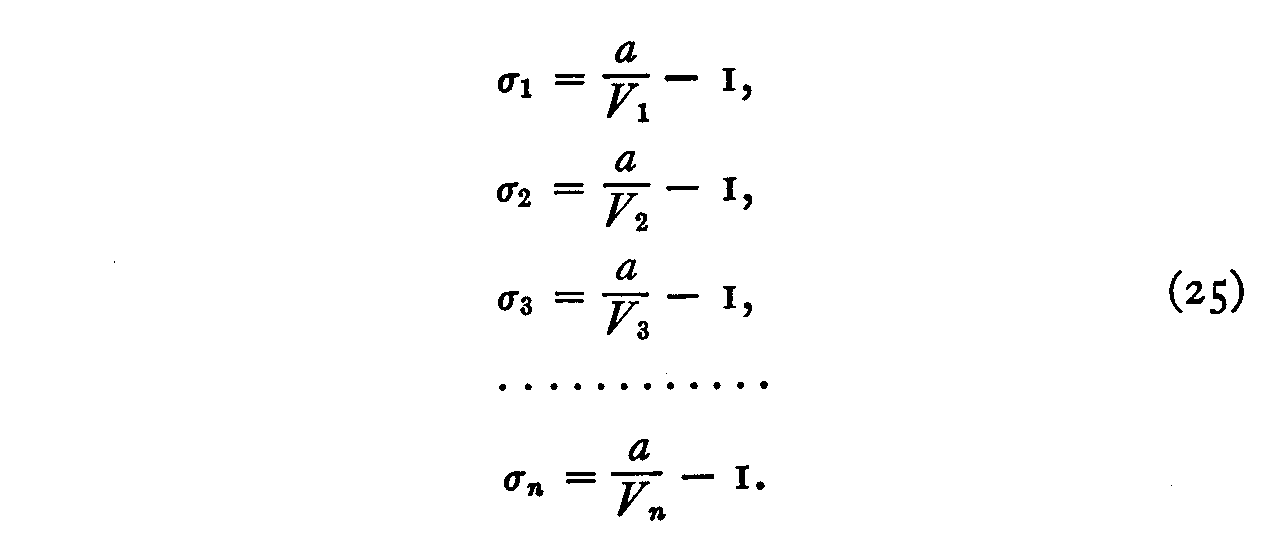
When the stimulus dispersions σl, σ2, σ3, . . . σn have been calculated, we may proceed with the calculation of the psychophysical values S1, S2, S3, . . . S.. This can be done as follows :
![]()
Summing, we have
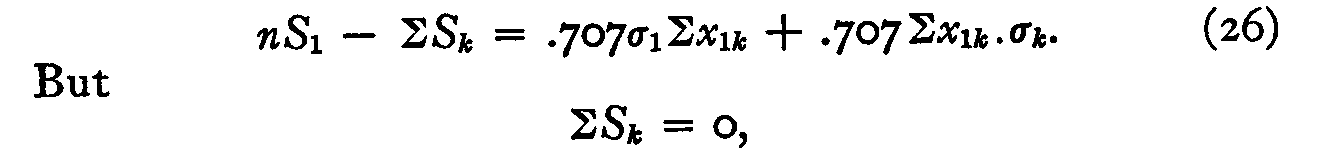
since we may place the origin at the arithmetical mean of the thirteen psychological values. Hence,
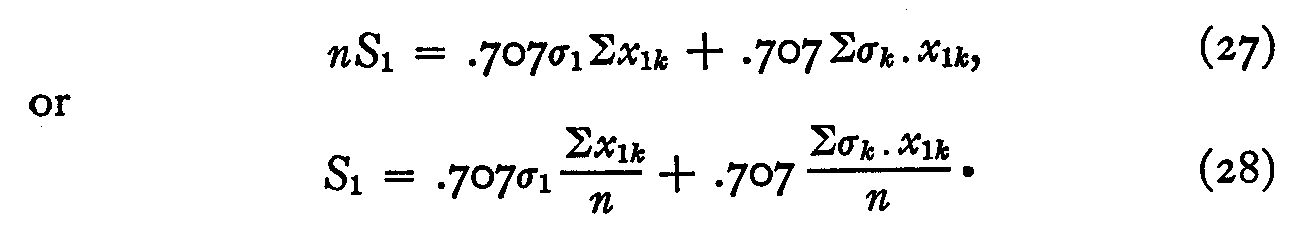
Let Mxl = mean of all values of x1k and similarly for each of the other stimuli.
Then
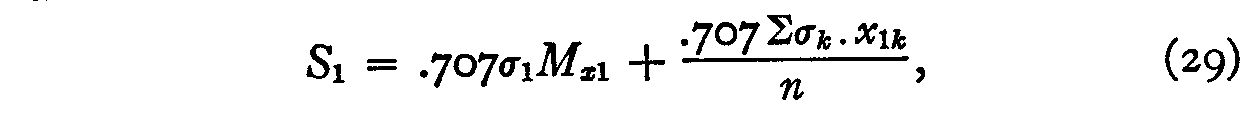
and a similar form can of course be written for each of the other stimuli.
The numerical work consists in calculating the standard deviations, V, of each column in Table II. Thus the standard deviation V of the first column is .4261. The sum of the reciprocals of these standard deviations is 26.3915 which
( 296) enables us to calculate the constant a by equation 24. It has a value of .98517. The stimulus dispersions can then be determined approximately by equation 25 and these have been recorded in column 6 of Table III for Case III. Their sum is 13, which is postulated in equation 22. The scale values in column 5 of the table are then computed by equation 29. Their sum is zero which satisfies the assumption of equations 26 and 27.
It will be seen in Table III that the discrepancies in scale value between Case III and Case V are in general largest for those stimuli that are found to have the largest stimulus dispersions and this is what should be expected, partly be-cause of the assumption in Case V that they are all equal and partly because of the assumption in Case III that they do not deviate markedly from unity.
The choice between the two cases should be made by noting which of them satisfies the experimental data with the least average discrepancy. With the thirteen scale values and approximate discrepancies calculated by Case III we can of course return to equation 2 for every pair of stimuli to calculate the proportion of the subjects who should prefer any one of the stimuli to any other. This has been done and the results are listed in the last column of Table III. The aver-age discrepancy between the experimental and the calculated proportions is 0.0249 which is smaller than the corresponding value for Case V.
SUMMARY
The numerical evaluation of the stimulus dispersions in the method of constant stimuli has been a troublesome problem. In this paper we have developed a procedure for obtaining an approximate value for the dispersion of each stimulus. The average discrepancy between the experimental and the calculated proportions is 0.0355 by Case V in which the stimulus dispersions are assumed to be equal but it is reduced to an average discrepancy of 0.0249 by Case III in which allowance is made for differences in stimulus dispersion. A criterion for deciding whether the simpler form of Case V or the more laborious Case III should be used for an experi-
( 297) -ment that has been conducted by the constant method is to plot pairs of columns of x-values in Table II. If the best fitting straight lines in these plots have a slope nearly equal to unity, then Case V can be used advantageously. If not, then a better agreement between experimental and calculated values will be obtained by Case III. In any event, the stimulus dispersions that are calculated by the procedure here described are approximate values. Their probable errors are undoubtedly large but the procedure does give a fairly good idea of the order of magnitude of the stimulus dispersions. For example, it is probably safe to assume that there is greater variation of attitude toward the Jews in our experimental population than for any of the other nationalities or races. This is found in the calculations according to which there is much greater variation in attitude toward the Jews than toward any of the other groups. It is approximately measured by the stimulus dispersion in Table III. This observation also agrees with the fact that the discrepancies for the Jews are much larger in Case V than for any of the other groups. In other words, the greater the deviation of the stimulus dispersion from the average dispersion of all the stimuli, the greater will be the error caused by the principal assumption of Case V and the greater will be the discrepancies between experimental and calculated proportions.
REFERENCES
1. THURSTONE, L. L., A law of comparative judgment, Psychol. Rev., 1927, 34, 273-286.
2. THURSTONE, L. L., A mental unit of measurement, Psychol. Rev., 1927, 34, 415-423.
3. THURSTONE, L. L., Three psychophysical laws, Psychol. Rev., 1927, 34, 424-432.
4. THURSTONE, L. L., Experimental study of nationality preferences, J. of Gen. Psychol., 1928, I, 405-425.
(Manuscript received April 20, 1931)