An Experimental Study of Nationality Preferences
Louis L. Thurstone[2]
Psychological Laboratories of the University of
Chicago and of
the Illinois Institute for Juvenile Research
The experiment here reported was designed as a rather severe test of the law of comparative judgment. This psychophysical law states the relation between the psychological separation of the stimuli (the sense distance) and the probability of correct discrimination on any single occasion. The law applies ideally to the situation in which a single observer makes several hundred discriminatory judgments for each possible pair of stimuli in any given stimulus series. The stimuli to which the law refers in its conventional psychophysical setting are the lifted weights, the grey papers, the line lengths, and the rest of the traditional stock-in-trade of the psychophysicist. The ideal situation above described constitutes Case I in the formulation of the law.[3] By a number of assumptions previously described, it is possible to apply the law to those situations in which a group of observers are used instead of a single observer and in which each member of the group makes only one discriminatory judgment for each possible pair of stimuli in the stimulus series. We shall here use the simplest form of the law, previously described as Case V.
'We shall also transfer the whole psychophysical reasoning from its traditional stimuli in which the subject responds to the question, "Which of these cylinders is the heavier?" (apologies for the stimulus error!) to the question, "Which of these two nationalities would you generally prefer to associate with ?" To transfer the application of the law from lifted weights to nationality preferences introduces
( 406) new factors into the judgments. The nationality preferences are saturated with prejudice and bias, with religious affiliations, and with wide differences in knowledge and familiarity. In addition to these variable factors, the group of 239 subjects was also intentionally left as heterogeneous as it was found to be among undergraduates at the University of Chicago. It is clear that with large proportions of Jews, Catholics, Negroes, Protestants, and students whose parents are foreign-born, it may be very questionable whether the distribution of attitude toward any one of the twenty nationalities is in any sense normal on the psychological continuum. However, when the calculated proportion of each judgment is compared with the corresponding experimental proportion, the average discrepancy is found to be only .03, which shows rather convincingly that the law of comparative judgment can be used for measuring not only the formal "sense distance" of conventional psychophysics but even so complex a continuum as the degrees of preference of a heterogeneous group of subjects for nationalities and races.
The experiment was performed by asking each of the 239 under-graduates to fill in a mimeographed schedule showing their racial and nationality preferences. The instructions on the schedule were as follows :
AN EXPERIMENTAL STUDY OF RACIAL ATTITUDES
This is an experimental study of attitudes toward races and nationalities. You are asked merely to underline the one nationality, or race, of each pair that you would rather associate with. For example, the first pair is:
Englishman—South American
If, in general, you prefer to associate with Englishmen rather than with South Americans, underline Englishman. If you prefer, in general, to associate with South Americans, underline South American. If you find it difficult to decide for any pair, simply underline one of them anyway. If two nationalities are about equally well liked, they will have about the same number of underlinings in all of the papers. Be sure to underline one of each pair even if you have to make a sort of guess.
American—Hindu
Englishman—Swede
Japanese—Italian
Hindu—Frenchman
Mexican—American
etc.
The list of pairs was continued so that every one of the twenty-one races or nationalities had been compared with every other one. This required
n(n—1)/2 =210
( 407) judgments which were mimeographed on three letter-sized sheets. The complete list of nationalities and races is given in the tables. In addition to these 210 judgments there were 21 repetitions, making a total of 231 pairs on the mimeographed forms. The purpose of the 21 repetitions was to verify empirically the probable errors of the proportions so that some estimate might be made of the probable error of the resulting scale values, both theoretically and empirically.
The law in the complete form is as follows :
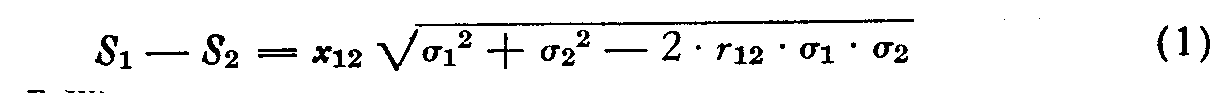
in which
(Sl – S2) = sense distance, i. e., the scale distance between the two modal discriminal processes. [4]
x12 = the sigma value corresponding to the observed proportion of judgments "Rl is greater than R2." R denotes the stimulus. The proportion is designated P1>2. The numerical value of x12 is positive when P1> 2 is greater than .50, and it is negative when P1> 2 is less than .50.
σ1 and σ2 = ambiguities (discriminal errors) of the two stimuli, R1 and R2.
r12 = the correlation between the discriminal deviations involved in the same judgment.
In the present study we have used Case V in which the law is applied to a group of observers, each observer giving only one judgment for every stimulus pair. In Case V it is also assumed that r12 = 0 and that the value of u is unity for every stimulus in the series. With these approximations the law takes the simpler form
![]()
when σ is chosen as the unit of measurement.
The first results are shown in Table 1. The interpretation of this table may be seen perhaps best by the following direct readings. Of the whole group, 89.8% preferred to associate with Americans rather than with Englishmen; 38.0% preferred to associate with Chinamen rather than with Japanese; 37.2% preferred to associate with Russians rather than with Italians. The rest of the table is interpreted in the same manner. These constitute the data on which our measurements will be based.
Our object is to calculate a scale value for each of the 21 nationalities. With these 21 scale values we shall prepare a table of 210 calculated proportions. The discrepancies between these two tables will be the criterion by which to judge the degree to which the law of comparative judgment is applicable to this type of data.
( 408)

( 409)

( 410) The first step is to ascertain the rank orders of the 21 nationalities. They are obtained by a simple summation of the proportions. These summations are given at the foot of each column in Table 1. The last row gives the absolute rank orders. The rank orders are: (1) American ; (2) Englishman ; (3) Scotchman, and so on.
These rank orders constitute a description of the group of undergraduates and it would vary from one group to another. In order to use this procedure for any interpretation regarding racial and nationality preferences, it is of course necessary to have a rather homogeneous group. Such a study is now being made with a large group of American-born students with American-born parents, and for several other rather homogeneous groups, similarly defined. Our present object is to test the measurement methods and it is a better test of our procedure to see how much internal consistency can be obtained with a heterogeneous group.
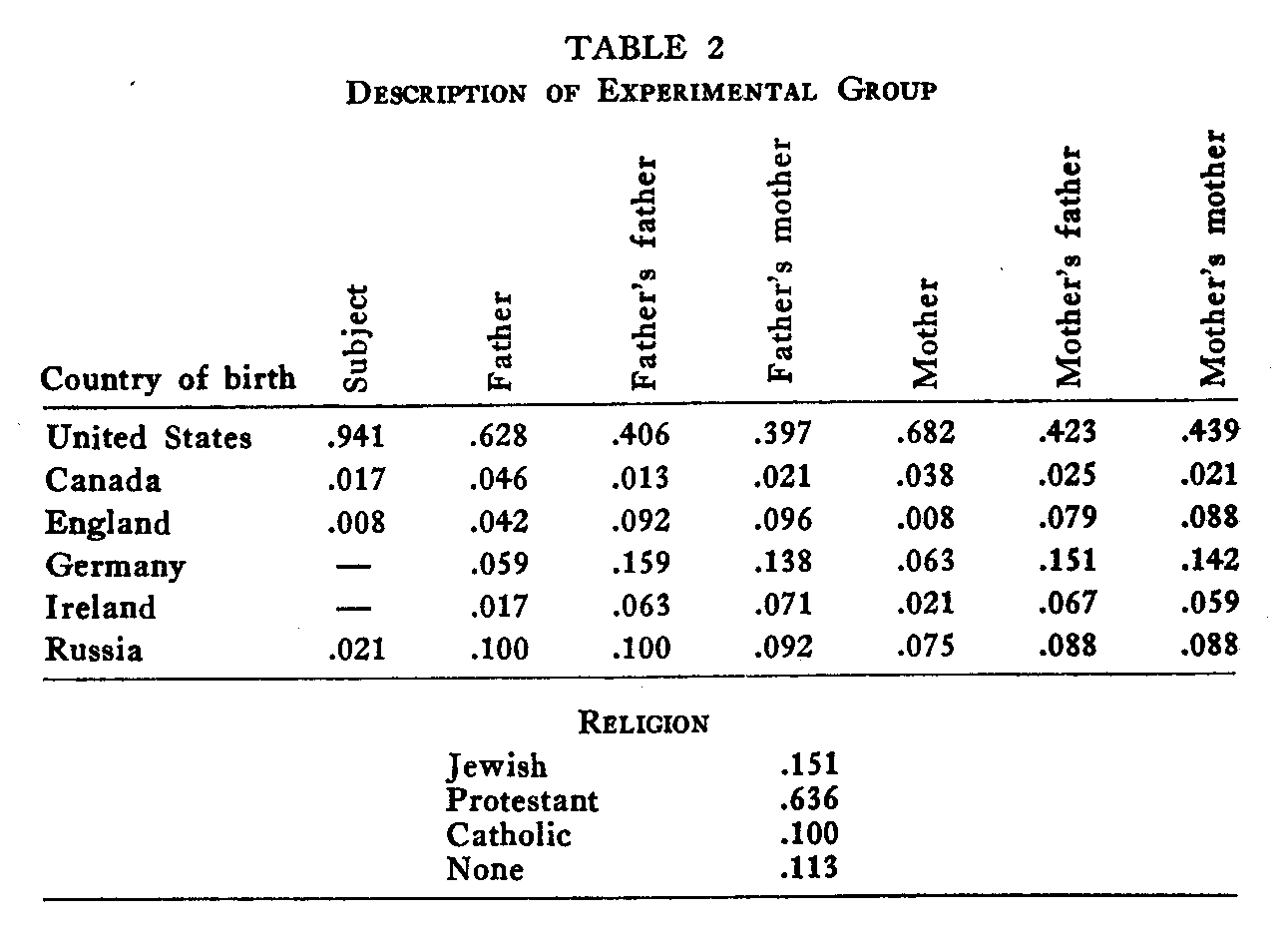
Some brief description of the group of undergraduates is in order because of the fact that the scale values of the nationalities naturally reflect the make-up of the group of subjects. Table 2 shows the representation of the principal countries among the 249 subjects.
The next step is to prepare a table of corresponding sigma values. This has been done in Table 3. Since the procedure of weighting is awkward in these calculations, we have merely dropped the most
( 411) unreliable proportions, namely those above .97 and those below .03. The rest are retained and are given equal weight in the calculations. It will be seen from the results that no serious damage is done by this additional approximation. The sign of each sigma value in Table 3 is positive when its corresponding proportion in Table 1 is above .50, and it is negative when the proportion is less than .50.
Let the scale values of the two nationalities whose scale separation is to be ascertained be designated S1 and S2 respectively. Let any other nationality be designated Sk. Then, by (2)
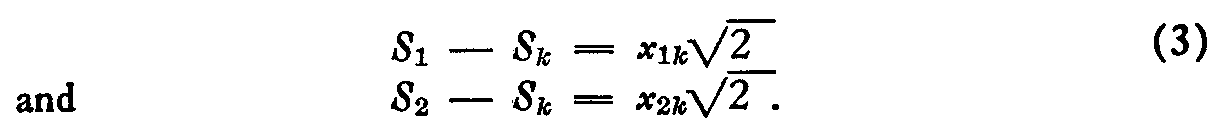
Subtracting,
![]()
Summing for all the nationalities, we have
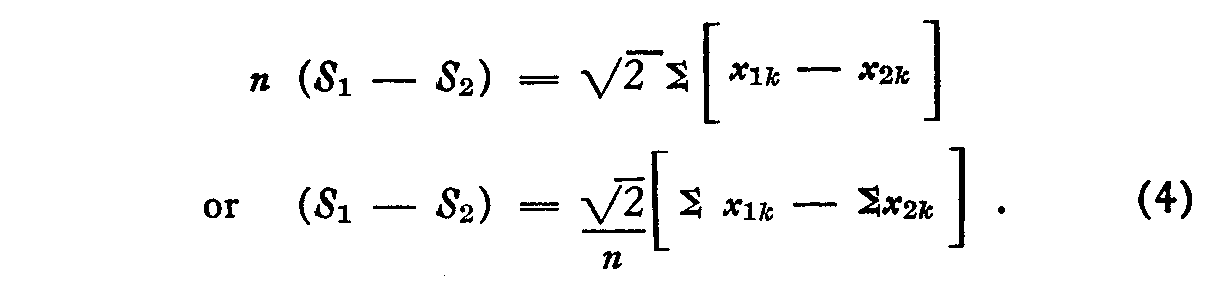
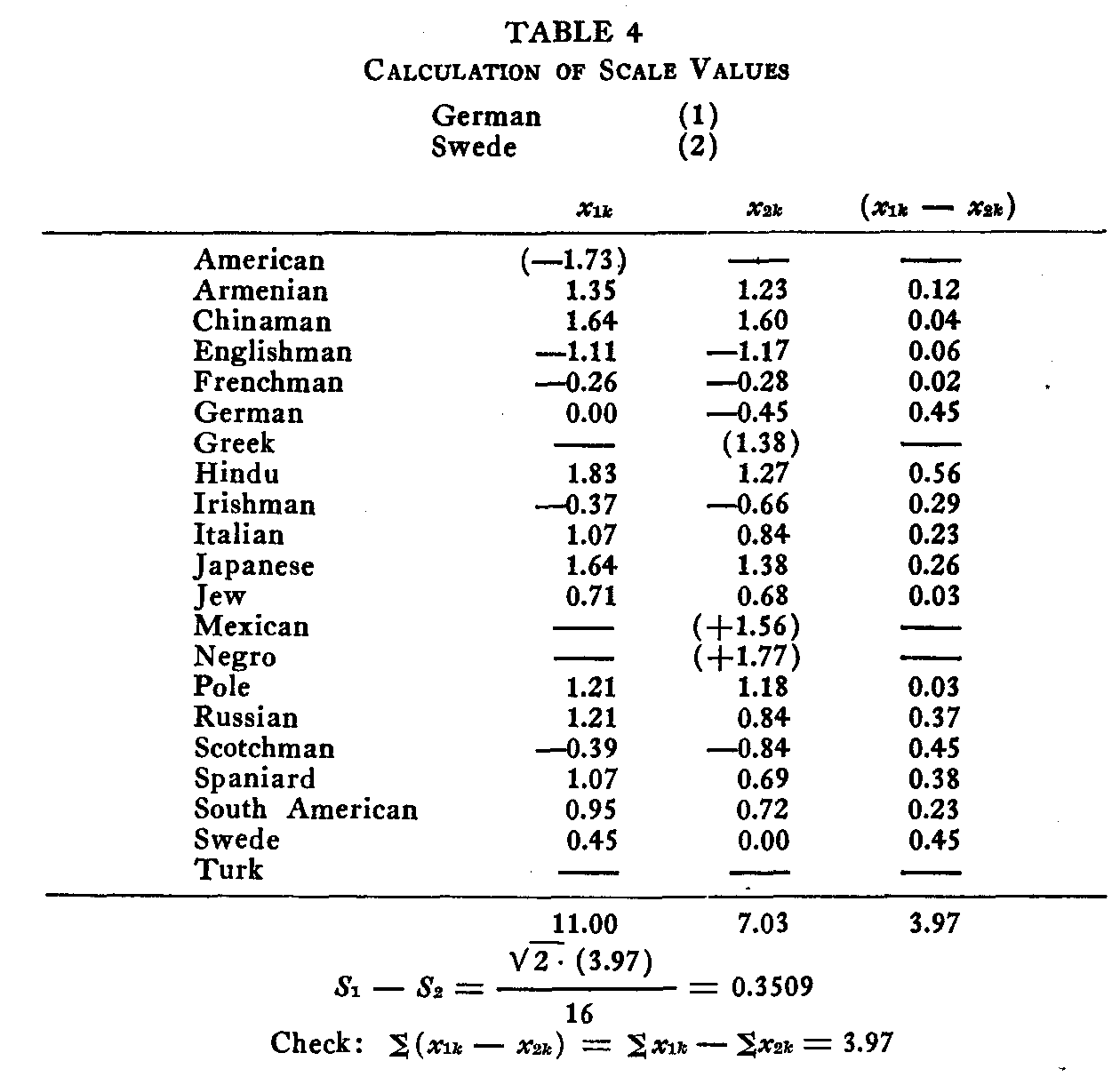
This enables us to ascertain the scale separation (S1 – S2) by making use of all the data. As an example of the application of the summation equation (4) Table 4 has been prepared. The first column is merely a list of the nationalities copied directly from Table 3. The second and third columns are copied directly from the columns "German" and "Swede" in Table 3.
The blank spaces in the second and third columns of Table 4 are transferred from Table 3. The entries in these spaces have been omitted from Table 3 because the proportions on which they are based are too unreliable, being either higher than .97 or lower than .03. In the fourth column of Table 4 are recorded the differences between the paired sigma values. Whenever one of the two sigma values is omitted, the corresponding difference is of course also omitted. The calculation of the scale separation between "German" and "Swede" is based therefore on the remaining sixteen pairs of sigma values as shown in the fourth column of the table. This fourth column is really inserted primarily for the purpose of check
( 412)

( 413)

( 414) on the arithmetical work because it is not needed logically for the calculation.
At the foot of Table 4 the substitutions in the summation equation (4) are shown. The arithmetical check on the calculations is also self-explanatory in this case. The scale separation between these two nationalities is 0.3509.
The order in which the scale separations are calculated is given by the absolute rank orders of the twenty-one nationalities shown
at the foot of Table 1. The first scale separation to be calculated was "American—Englishman." The second was "Englishman—Scotchman." The successive pairs are chosen from the absolute rank order of Table 1. Consequently there were twenty tables like Table 4 in the present study.
Theoretically, it should be possible to ascertain the scale separation between any two nationalities in the whole list even though they are quite far apart on the scale, but such a procedure would be based
( 415) on a small number of paired sigma values, many of them dropping out because of low reliability. If two nationalities are widely separated on the scale, there will be so many proportions of zero and 100% that the scaling cannot be satisfactorily made. A least square solution could be laid out which would take into consideration all of the proportions in the whole of Table 1 with a system of weights but the solution would be prohibitive. It would require the solution of a set of twenty normal equations with as many unknowns. Such a procedure is not feasible. For that reason the scale separations are determined for pairs of nationalities that are adjacent in absolute rank order.
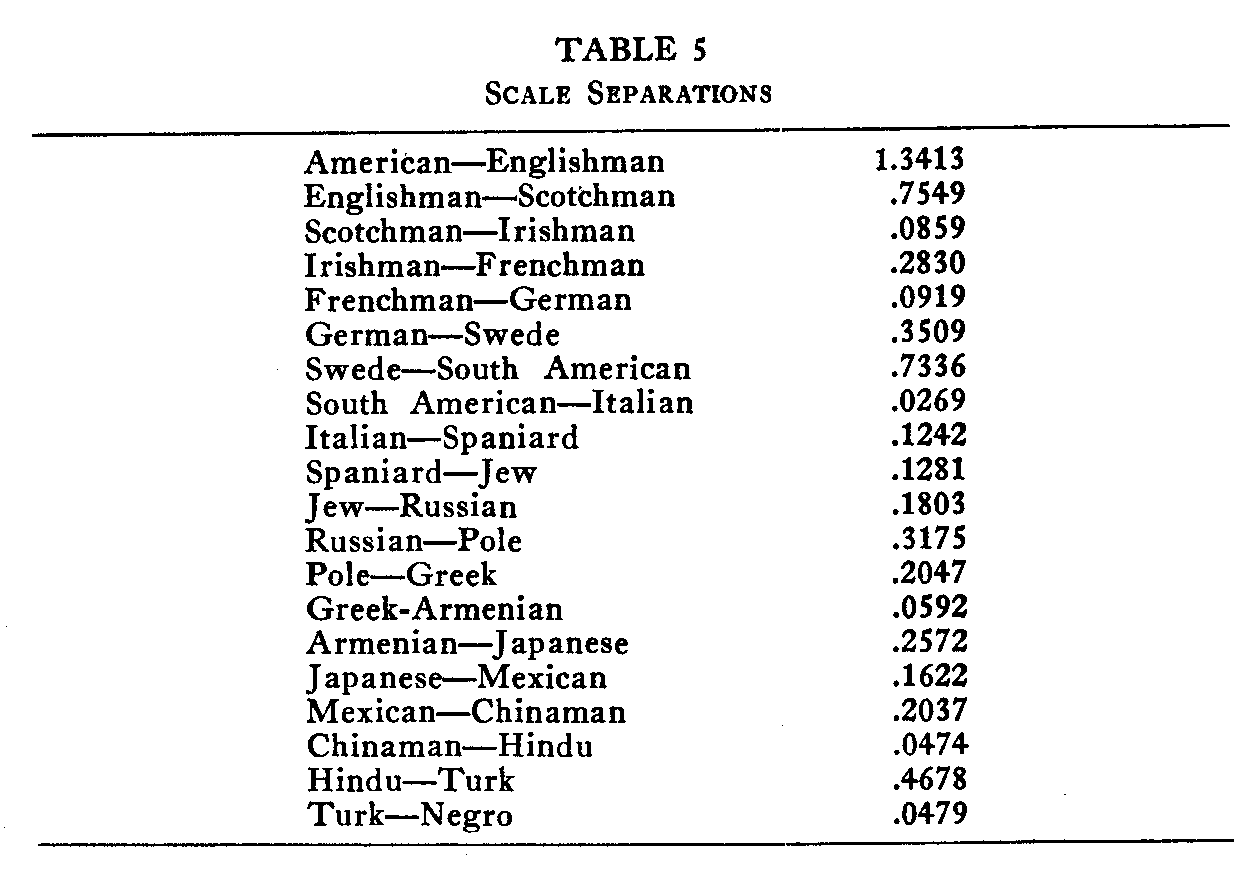
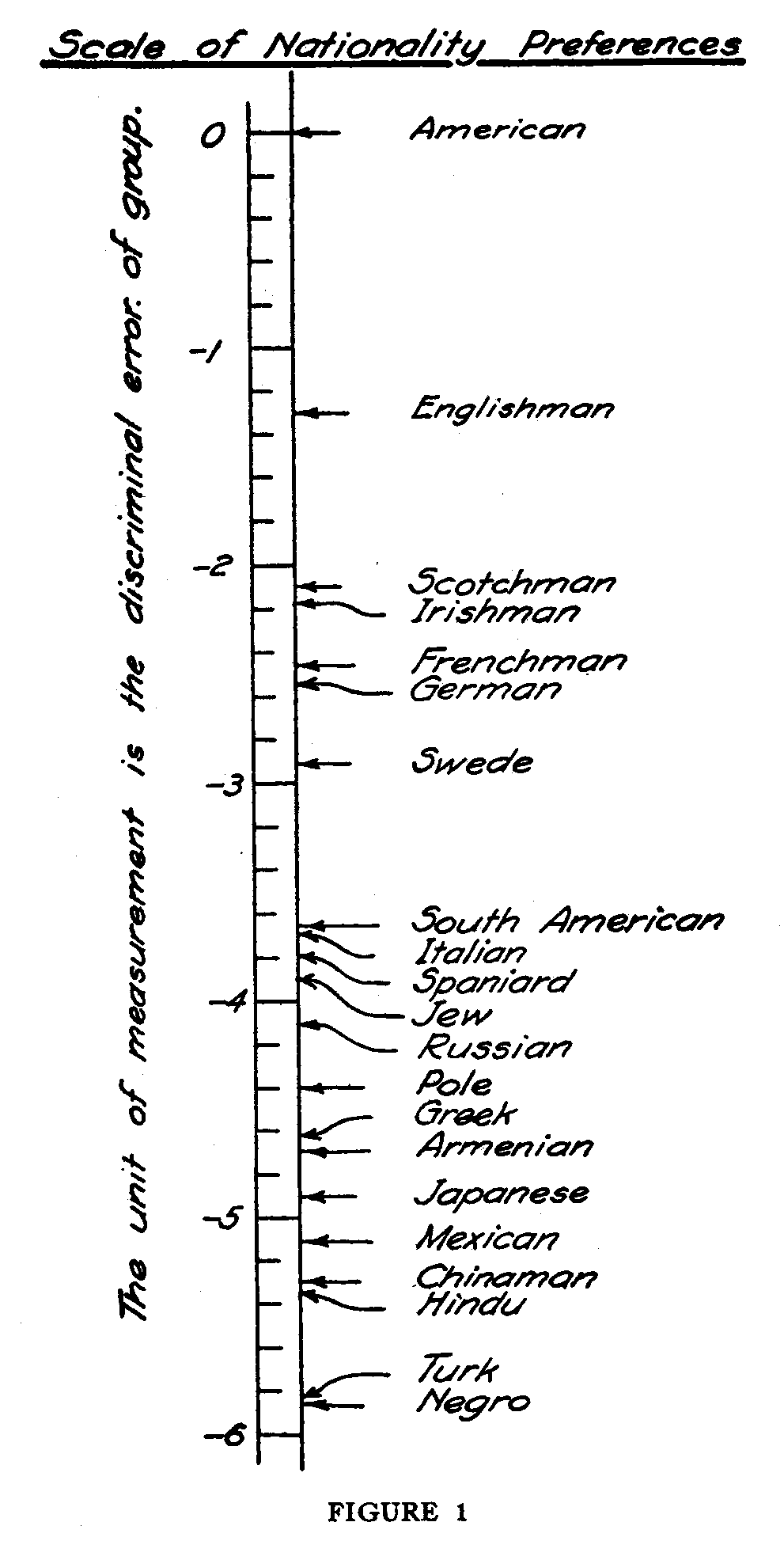
In Table 5 we have a list of the scale separations of the twenty pairs of nationalities which have been calculated by the procedure shown in Table 4. The next step is to adopt the scale value of one of these nationalities as an origin. The scale value of "American" was chosen as an origin and, since all other nationalities are preferred less often by our subjects, all of the other scale values are negative. In Table 6 the final scale values have been recorded. They are obtained directly from the scale separations of Table 5 with the scale value of "American" set at zero. It is of course clear that we are here dealing with a scale in which the origin is quite arbitrary. The law of comparative judgment gives the scale separation but says nothing about measurement from any origin.
In Figure 1 the scale values of Table 6 have been represented
( 416)

graphically, but it should be borne in mind that this figure represents merely the distribution of attitude toward these various nationalities in the particular group of this study. If we should want to compare the attitudes of two groups, it would be possible to scale the same list of nationalities for both groups separately and then to correlate the two sets of scale values. A high correlation between the two sets of scale values would show objectively that the two groups have very similar attitudes toward the nationalities in question while a low correlation would indicate that the two groups are very different in their national preferences. It would, in fact, be rather interesting to make such comparisons for representative groups of students at the universities in different countries and such a study is now being planned.
If two groups were to be compared in the manner suggested above, it is conceivable that the two scales would differ considerably in the range of scale values. The present group of subjects has a range of nearly six sigma for the whole list of twenty-one nationalities. Now, if another group should have a range of, say, only three sigma, it would indicate that the latter group is more international in its attitudes, more tolerant of national differences. A wide range of scale values indicates rather strong and rather uniform national preferences. An internationally minded group would give proportions hovering more closely about .50 and hence the scale separations would be, on the whole, smaller than the scale separations for a prejudiced
( 417)
(418) group. We have here a psychophysical tool for making objective the national attitudes of a group. It is conceivable that the method may be of some use in the objective measurement of social attitudes that are usually reported with the prejudice or bias of individual authors and investigators.
With the twenty-one scale values before us in Table 6, we want to ascertain how much internal consistency we may have in such a scale. In order to test for internal consistency we shall use the scale values as the basis for a set of calculated proportions which may be compared with the experimental proportions from which we started. We return to equation (2). With the scale values known we may calculate the value of x12 and this may be converted into the corresponding proportion by the aid of a probability table. This will be the calculated proportion which is to be compared with the corresponding experimental proportion. An example of the calculations is shown in Table 7. The first column contains the list of nationali-
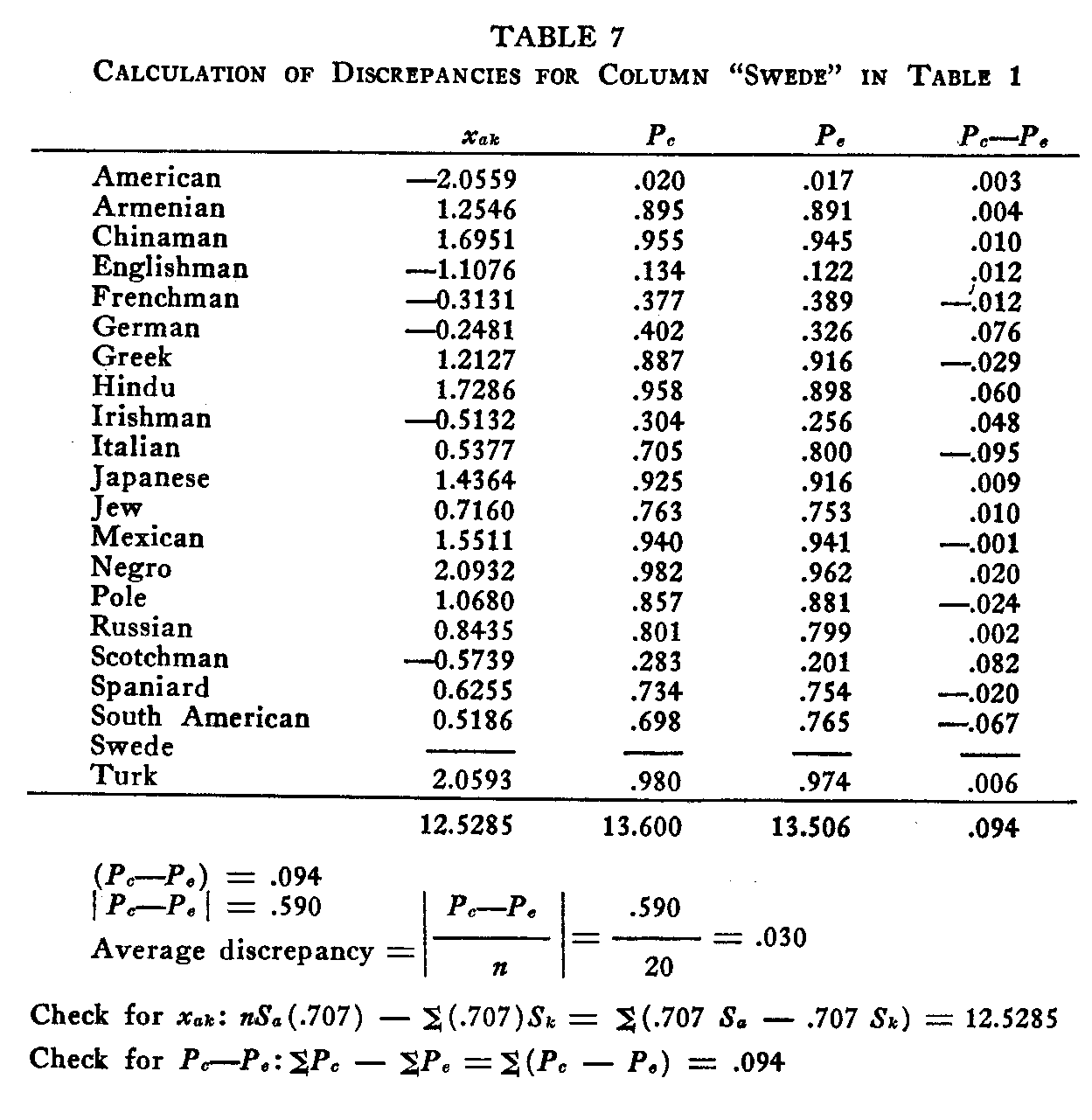
(419) -ties as in the previous tables. The second column gives the calculated value of
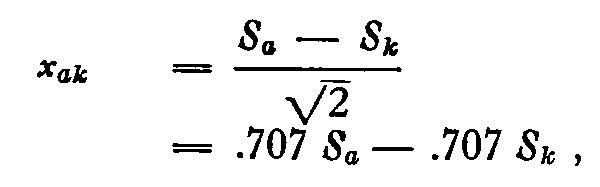
in which
xak = the sigma value of the calculated pro-portion of subjects who should prefer nationality "a" rather than nationality "k."
Sa = the scale value for "Swede."
Sk= the scale value of each of the other nationalities in turn.
Consequently, the second column in Table 7 will be calculated by the formula
xka
= .707 X 2.9079 — .707 Sk
= 2.0559 — .707 Sk.
The next column gives the calculated proportion, Pc corresponding to the calculated value of xak. It is obtained directly from the Kelley-Wood tables. Adjacent is the experimental proportion, Pc obtained from Table 1. The discrepancy between the experimental and the calculated proportions is shown in the last column of Table 7. The average discrepancy for the whole column is calculated at the foot of the table. The last column of the table is inserted partly to enable one to inspect the discrepancy for each pair of nationalities and also for the purpose of arithmetical check on the calculations. The average discrepancy for the twenty nationalities compared with "Swede" is .03 which happens to be the same as the average discrepancy between Tables 1 and 8. The calculations in this study involved twenty-one tables like Table 7, one for each column of Table 1. The average discrepancy of .03 for the twenty comparisons with "Swede" is shown at the foot of the column "Swede" in Table 8. The last row of Table 8 shows the average discrepancy for the twenty comparisons with each nationality.
Inspection of the discrepancies for the different nationalities reveals that the highest discrepancy of .06 occurs for "Jew." Since 15% of the subjects were Jews and since the prejudice against them is common among other members of the group, it is quite probable that the distribution of attitude toward the Jews in this group of subjects deviates considerably from the normal probability curve. It might even be bimodal. Even if the distribution can be represented roughly as bell-shaped, its dispersion would probably be larger in this group than the dispersion for other nationalities. Either one of these factors would cause a noticeable discrepancy between the experimental and the calculated proportions because our procedure in Case V as-
( 420)

( 421)

( 422) -sumes that the distribution of attitude toward each nationality is normal and that the dispersions are the same for all of the nationalities and races.
The average discrepancy between Tables 1 and 8 is shown in the last row of Table 8 to be .0299 or practically three per cent. It is very satisfactory considering the fact that the equation that has been used for the scaling contains a number of assumptions that are undoubtedly only roughly approximated by the data.
There were twenty-one repeated pairs in the original mimeo-graphed forms on
which the nationality preferences were recorded by the 239 subjects. These
repetitions were so arranged that every nationality was represented twice in the
twenty-one repeated pairs. The repetitions were scattered at random throughout
the lists so that the subject would have slight opportunity to recall his first
judgment on a particular pair if he was at all in doubt. The object of these
extra or repeated pairs was to ascertain the average error of the original
proportions themselves so that these might be compared with the magnitude of the
discrepancies between the experimental and calculated proportions. The average
difference between the two proportions of the repeated pairs was .019 or nearly
two per cent. When this error of the original proportions is compared with the
discrepancy between the experimental and calculated proportions which was .0299
or practically three per cent, it is seen that the psychophysical method here
described fits the data with surprising ac-curacy. In fact, the average
discrepancy of two per cent in the original experimental proportions accounts
for a part of the discrepancy between the experimental and the calculated
proportions.
SUMMARY
1. The principal object of this study is to show that psycho-physical formulations which are made ideally for discriminatory judgments of simple physical stimuli can be applied also to discriminatory judgments involving social values even when these values are loaded with prejudice or bias. The law of comparative judgment in its simplest form, Case V, is here applied to discriminatory judgments of preference for nationalities and races. The group of 239 subjects was intentionally heterogeneous in that 40% or more of the parents and grandparents were foreign-born, 15% were Jews, 64% were Protestants, and 10% were Catholics.
2. The method of paired comparison was used as the experimental procedure. A proportion of judgments of preference was determined for every possible pair of nationalities. On the basis of these experimentally observed proportions the scale value of each nationality or race was calculated by the law of comparative judgment. These are shown graphically in Figure 1.
( 423)
3. The internal consistency of the calculations is shown by the discrepancies between the experimental and the calculated proportions. The average discrepancy between them was only three per cent. The average difference between the repeated proportions in the original form was two per cent.
4. The law of comparative judgment can be used for measuring objectively the degree of similarity between two groups as regards their national and racial attitudes, prejudice, or bias. This is accomplished by correlating the scale values of the same list of nationalities for both groups. If the correlation coefficient is high, the two groups are similar in their attitudes toward nationalities and races. If the coefficient is low, they are different in their national and racial preferences.
5. Another application of the law of comparative judgment is in the quantitative measurement of the degree of tolerance of a group for the nationalities in the list. Any measure of the scatter of scale values for the whole list can be used as a quantitative index of the tolerance of the group. 'When the scatter is wide, the tolerance is low. When the scatter 'is small, the group is correspondingly more tolerant.
6. The law of comparative judgment can be used to describe objectively the
attitudes of a group of subjects toward nationalities and races. The same method
can undoubtedly be used also for describing the attitudes of a group toward
other social values which are saturated with prejudice and bias. The method is
free from the effects of the personal bias of the individual investigator. It is
hoped that psychophysical tools may find application not only in the restricted
field of sensory discrimination but also in the study of other psychological and
social values.
University of Chicago
Chicago, Illinois