Psychophysical Analysis
Louis L. Thurstone
The purpose of this paper' is to present a new point of view in psychophysics and to trace some of its implications. In the determination of a difference limen, the psychophysical judgment, no matter which of the classical methods is followed, is traditionally considered to be a function of two factors, namely, (1) the separation or difference between the two physical stimulus magnitudes, and (2) a discriminatory power measured in terms of sense distances or just noticeable differences. The psychological continuum, no matter what it may be called, is supposedly determined by these just noticeable differences or equal appearing intervals, which are by definition assumed to be equal. The stimulus magnitudes are laid out on this continuum as landmarks, and the psychological separation between them is stated in terms of just noticeable differences or equal appearing intervals.
It will lead to a rather more flexible and illuminating analysis if we start out a little differently. I shall suppose that every psychophysical judgment is mainly conditioned by four factors, namely, the two stimulus magnitudes or the separation between them, the dispersion or variability of the process which identifies the standard stimulus, and the dispersion or variability of the process which identifies the variable stimulus. The present analysis will concern these variables and finally the experimental procedures by which they may be isolated.
At the outset it may be well to make clear some things that will not be assumed. I shall not assume that the process by which an organism differentiates between two stimuli is either psychic or physiological. I suppose it must really be either, or perhaps both, but it is indifferent for the present argument whether the processes by which we identify or discriminate grays and loudnesses and handwriting specimens are mental or physiological. Hence this analysis has nothing really to do with any psychological system. I shall try not to disturb the main argument with systematic irrelevances or with my personal notions regarding the psychic or physiological nature of the psychophysical judgment.
Further, I shall not assume that sensations, or whatever the identifying and discriminating functions may be called, are magnitudes. It is not even necessary for the present argument to assume that sensations have intensity. They may be as qualitative as you like, without intensity or magnitude, but I shall assume that sensations differ. In other words, the identifying process for red is assumed to be different from that by which we identify or discriminate blue.
A term is needed for that process by which the organism identifies, distinguishes, discriminates, or reacts to stimuli,
( 369) a term which is innocuous and as noncommittal as possible, because we are not now interested in the nature of the process. "Sensations," or more generally, "subjective conditions," would be good terms, but "physiological states" or "intraorganic conditions" would also be satisfactory. In order to avoid any implications, I shall call the psychological values of psychophysics discriminal processes. The psychophysical problem concerns, then, the association between a stimulus series and the discriminal processes with which the organism differentiates the stimuli.
In Figure 1 let the circles Rl, R2, R3, R. represent a series of stimuli which constitutes a continuum with regard to any prescribed stimulus attribute. It is not necessary to limit psychophysical analysis to stimuli which have intensity or magnitude as their principal attribute. For example, a series of handwriting specimens may be arranged in a continuum on the basis of general excellence. They would of course arrange themselves in a different continuum if some other attribute were specified, such as size of letters, legibility, coarseness of pen, or what not. Similarly, a series of spectral colors may be
( 370) arranged in a continuum for discrimination of brightness, chroma, saturation, apparent remoteness from red, or what not. Psychologically, some of these attributes can be measured, while physically the measurement may even be impossible. We are assuming, then, that a series of stimuli has been arranged in a continuum according to any attribute about which one can say "more" or "less" and that psychophysics need not be limited to stimuli which have magnitude or size, such as lifted weights and the brightnesses of grays.
Referring again to Figure 1, suppose that each stimulus in the series has a discriminal process which is a psychic or physiological function of the organ-ism. Thus the stimulus R6 has a discriminal process S6 with which the discrimination of the stimulus takes place. These discriminal processes, whatever be their nature, can be labeled only in terms of their corresponding stimuli, so that the discriminal process S6 is labeled by the stimulus R6 with which it is associated. In the same manner the other discriminal processes in the series may be labeled by the stimuli which produce them. Naturally the discriminal processes would arrange themselves in a totally different order by changing the attribute of the stimuli by which they are arranged in a continuum. We have then two continua, one for the stimuli and one for the discriminal processes of these stimuli. The stimulus continuum must, of course, be defined in terms of some definite stimulus attribute. The discriminal continuum is a qualitative one which does not necessarily have either magnitude or intensity.
There is, of course, no possibility of recording experimentally in any direct way these discriminal processes that correspond to a series of stimuli. It is possible, however, to make some interesting inferences about the psychological continuum indirectly. The stimuli may be used to designate locations in the psychological scale just as though the stimuli, or their names, were used as tags or landmarks in a continuum which has otherwise no identifying marks or mileposts. It is the relative separations between these landmarks on the qualitative psychological continuum which it is the central problem of psychophysics to survey. In the figure there is no attempt to indicate quantitatively the relative separations between the stimuli or between their psychological correlates. The diagram indicates only that for each of the stimuli in the stimulus continuum one may postulate a discriminal correlate and that these psychological correlates also form a continuum of some kind. Nothing more is known, for the purposes of measurement, about the psychological continuum except that a discrete series of discriminal processes of unknown nature can
( 371) be used as landmarks along its course and that these processes or landmarks are experimentally controllable or identifiable only in terms of the physical stimuli that produce them.
So far the argument has proceeded as though there were a fixed one-to-one relation between the stimuli and their respective psychological correlates. It may be assumed that this relation is not so fixed as might be indicated by Figure 1. It undoubtedly happens that stimulus R6, for example, does not always produce the same discriminal process S6. The present method of psychophysical analysis rests on the assumption that constant and repeated stimuli are not always associated with exactly the same discriminal process but that there is some qualitative fluctuation from one occasion to the next in this process for a given stimulus. This raises an interesting possibility. It might happen, for example, that stimulus R6 has ordinarily S5 as its discriminal process but that sometimes the qualitative fluctuations would spread to S4 or to Ss. It might even happen, although rather seldom, that the stimulus R5 would have as its process Ss or S7. It should be recalled that each of these processes or qualities is identified by that stimulus which most frequently produces it, so that S4, for example, is habitually associated with R4 and so on. This is the fundamental idea of the psychophysical analysis of the present paper.
The variability of this connection between the stimulus and its discriminal process works both ways. A given process S5 would be associated most frequently with R5 but occasionally also with adjacent and closely similar stimuli in the stimulus continuum, such as Rs, R4, R6, R7. Similarly, the stimulus R5 can be thought of as most frequently associated with the process or quality S5 but occasionally with the adjacent qualities, such as Ss, S4, S6, S7. Since the discrimination between stimuli is made in the processes of the psychological continuum, we shall be concerned with the latter of these two regressions, namely, the qualitative fluctuations in the discriminal processes that are associated with a constant and repeated stimulus.
The psychophysical relations may be summarized, so far, in the following propositions.
(1)A series of stimuli R1, R2, Rs . . . Rn can be arranged in a continuum, with reference to any prescribed quantitative or qualitative stimulus attribute.
(2)These stimuli are differentiated by processes of the organism of unknown nature, and they are designated Si, S2, Ss . . . Sn,, respectively. Every stimulus Rk is identified by the organism with the process Sk● These processes may
( 372) be either psychic or physiological or both. In this discussion they are referred to as the discriminal processes or qualities.
(3)When the discriminal processes Sl. . . S are considered in the same serial order as the corresponding stimulus series, they constitute what may be called the discriminal continuum or the psychological continuum. This continuum is the correlate of the already postulated stimulus continuum.
(4)It is assumed that the correspondence Rn — S is subject to noticeable fluctuation, so that Rn does not always produce the exact process Sn. but sometimes nearly similar processes S+1or S,_7and sometimes even S.4-2or Sn_2. It goes without saying that the numerical subscripts are here used to denote qualitative similarity and that no quantitative attributes are thereby necessarily injected into the discriminal processes. This fluctuation among the discriminal processes for a uniform repeated stimulus will be designated the discriminal dispersion.
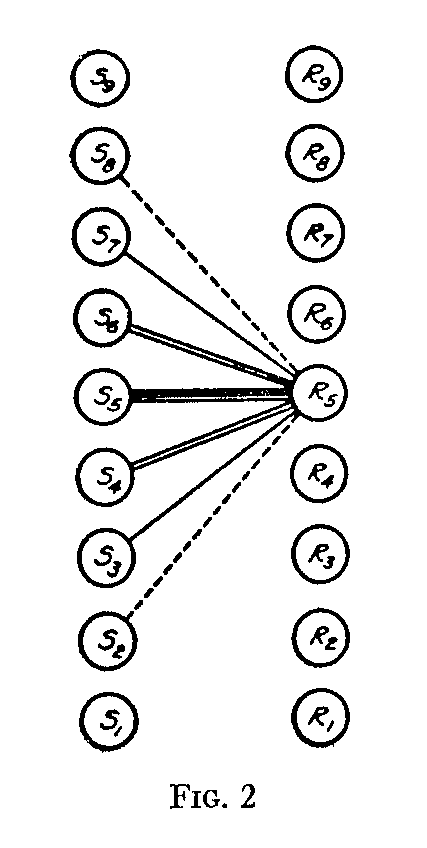
In Fig. 2 are represented the two continua, one for the stimulus series and one for the corresponding discriminal processes. Let R5 be one of the stimuli in the stimulus series. It is assumed that some discriminal process S5 occurs more frequently with this stimulus than any of the other processes. Hence it is designated the modal discriminal process for that stimulus. In this sense S5 is the modal discriminal process for the stimulus R5, and so on.
The relative frequencies of the different processes are represented for stimulus R5 in a rough diagrammatic way. Thus there are three lines connecting R5 with S5 to indicate the relation between the stimulus and its modal discriminal process. There are only two lines connecting the adjacent processes with the same stimulus R5, and this represents the relatively lower frequency of this association. The processes S3 and S7 are connected with the same stimulus with only one line to represent relatively infrequent association. Finally, the dotted lines represent in the same manner very infrequent association between the processes so marked and the stimulus R5. The extreme processes without connection with R5 represent, then, those processes which are so different from the modal process for Rs that they never occur in association with the given stimulus or that such association would take place only under unusual conditions as affected by practice, fatigue, sensory adaptation, successive or simultaneous contrast, and so on.
The simplest and perhaps the most obvious plan for scaling would be to assign linear values to the discriminal processes, with reference to a given stimulus, inversely proportional to the frequencies with which these processes occur with the given stimulus. With Rs as the given stimulus in Figure 2 the reckoning would start with the corresponding modal process Ss as an origin or datum. For this stimulus the other processes could be assigned distance values from S5 inversely proportional to their frequencies of occurrence with the given stim-
( 373) -ulus. Any plan that might be adopted is subject to experimental test in that the separations between the processes can be scaled with reference to each of the various stimuli. Naturally these scale distances between the processes should remain practically constant, no matter what the stimulus may be, in order to have a valid measuring method. Experimental test shows that the plan just suggested of assigning distance values on the psychological continuum breaks down. It is found that the separations between the processes do not retain stable values when they are determined for different stimuli. Therefore some other plan must be adopted.
The normal probability curve has been so generally abused in psycho-logical and educational measurement that one has reason to be fearful of criticism from the very start in even mentioning it. The only valid justification for bringing in the probability curve in this connection is that sit presence can be experimentally tested. The writer has found experimentally that the normal probability curve was not applicable for certain stimuli. In most of the experiments the distributions are reasonably close to normal.
Since the assumption of a normal distribution for the discriminal dispersion can be experimentally verified and limited to those stimulus series where its reality can be tested, it will be reasonable to make this assumption subject to verification in every case. The hypothesis can be stated as follows: The discriminal dispersion which any given repeated stimulus produces on the psychological continuum is usually normal. The frequencies with which the discriminal processes occur for a given stimulus ordinarily describe a normal distribution when plotted on the psychological continuum as a base. In experimental practice the procedure is the reverse of this hypothesis because the frequencies are known first experimentally, and from these frequencies we construct the psychological continuum. The writer has found in several studies that the separation between any pair of processes remains practically constant no matter which of the neighboring stimuli is used as a base for the calculation. Such is not the case, however, when the separation of any pair of processes is assigned values directly or inversely proportional to their frequency of occurrence.
In Figure 2, where R5 is chosen as the stimulus, we should therefore, according to this hypothesis, assign scale values to the various processes as distances from S5 as an origin. These distances would be assigned in terms of the standard deviation of the distribution of process frequencies. There is, of course, no further unit in terms of which this standard deviation can be ex-pressed. It is itself a unit of measurement because all that we can do with the psychological continuum is to lay off linear separations between the processes proportional to their true value, since, so far as we know, there is in the nature of
( 374) the case no further absolute unit of measurement for the psychological continuum. But we shall see that it is possible to compare the discriminal dispersions for two stimuli and to determine experimentally the ratio of any two of these dispersions. Psychological measurement depends, then, on the adoption of one of these dispersions as a base and the use of its standard deviation as a unit of measurement for the psychological continuum under investigation.
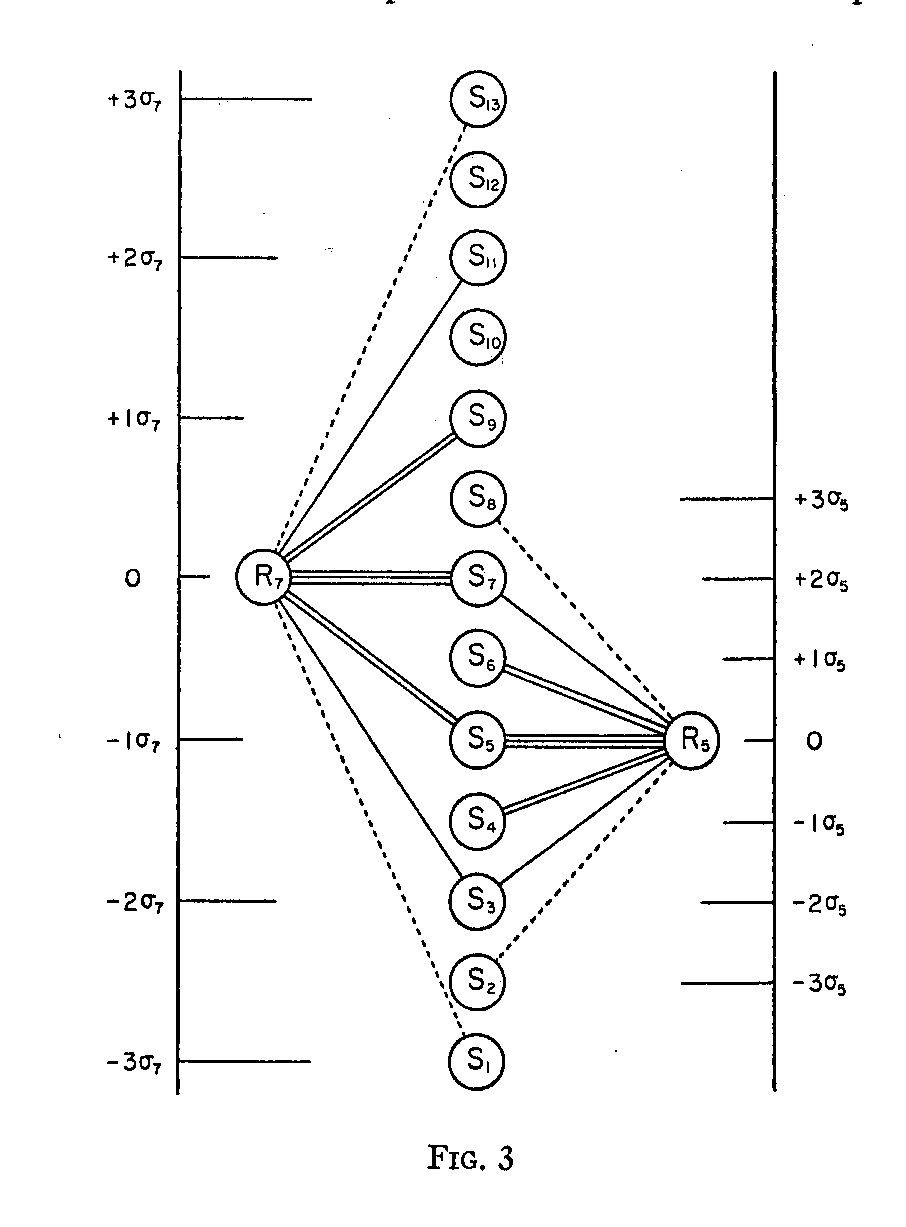
In Figure 3 let the column of thirteen circles represent so many discriminal processes, each of them being a modal discriminal process for a stimulus with the same numerical designation. Two of these thirteen stimuli are indicated in the figure, namely, R5 and R7. Suppose that these stimuli are arranged in a continuum according to any prescribed stimulus attribute, and let R7 be more ambiguous, or less sharply defined, than R5. An example would be two specimens of handwriting, one of which would be a beautiful but unusual handwriting, or perhaps it might be written in a foreign language,
( 375) or it might be in German script, which would possibly call forth judgments influenced by prejudice from factors other than those of the hand-writing characteristics. If the experiment involves the comparison of loudnesses, a variation of the certainty or ambiguity of judgment for a particular stimulus might be caused by variations in timbre or pitch. Ordinarily, psychophysical experiments are so set up as to avoid, as completely as possible, the introduction of extraneous factors to influence the ambiguity of judgment, and the stimuli are made into as homogeneous a series as may be experimentally possible.
In Figure 3 the two stimuli are represented as differing in the certainty with which they can be judged as to the prescribed attribute for the stimulus continuum, and R7 is indicated as the more variable or uncertain of the two. The modal discriminal process for R7 is S7as before, and the discriminal processes S5, S5, SI might be assigned deviation values of 1σ,
( 376) 2σ, 3σ, respectively, from S7 as a datum. These deviation values would be assigned on the basis of the frequency with which each of these processes occurs with R7 as a stimulus. With the same diagrammatic representation let the other processes be assigned their deviation values from S7as a base, and let the same processes be assigned frequency-deviation values from S5as a base for stimulus R5. In Figure 3 these hypothetical deviations are given numerical values. Note from the figure that the discriminal process S5 which is modal for stimulus R5 has a deviation value of -10-7 for stimulus R7. Similarly, the discriminal process S4 has a deviation value of -1.50-7 for stimulus R7, while it has a deviation value of -10-5 for stimulus R5. If this analysis is correct, it should happen not infrequently that the stimuli which constitute a continuum according to any prescribed stimulus attribute are subject to varying degrees of dispersion when they are perceived or judged. Some stimuli are probably placed with reference to the prescribed attribute more accurately and consequently with a smaller discriminal or subjective dispersion than other stimuli. It is probably true that this variability of the discriminal dispersion on the psychological continuum is of relatively less serious importance in dealing with strictly homogeneous stimulus series, but it becomes a serious factor in dealing with less conspicuous attributes or with less homogeneous stimulus series, such as handwriting specimens, English compositions, sewing samples, oriental rugs. In measurements of the type known as judgment scales the discriminal dispersion on the psychological continuum becomes one of the unknowns to be determined as well as the scale value of the specimen. Every specimen in such a series presents two unknown values to be determined, namely, the scale value of its modal discriminal process on the psychological continuum and its discriminal dispersion.
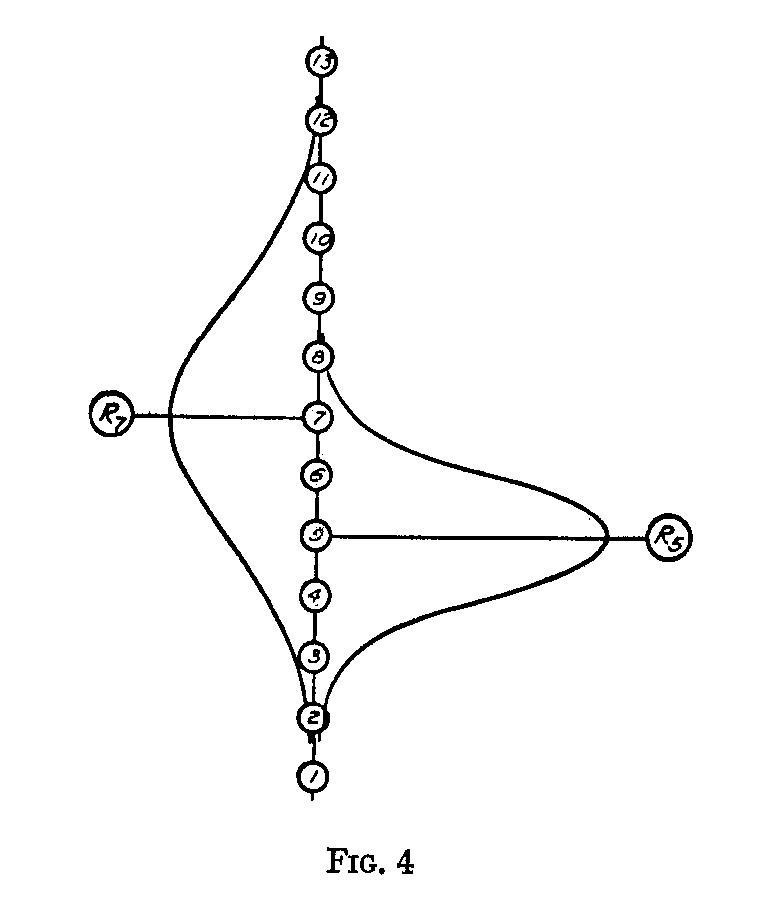
Instead of the diagrammatic representation of Figure 3, two normal probability curves may be substituted, subject of course to subsequent experimental verification. This has been done in Figure 4. Here the psychological continuum has been constructed on the hypothesis that the discriminal processes describe a normal distribution when plotted on that continuum. When R7 and R5 are presented for a comparative judgment, each of the stimuli produces a discriminal process of some kind, and the certainty of the discrimination may be assumed to be mainly a function of the difference between these two processes. If R7 happens to be associated with one of the processes at the upper range of its discriminal dispersion and if R5 happens to be associated with one of the processes at
( 377) the lower end of its discriminal dispersion, then the discrimination is made with ease and the judgment is correct. If these conditions are reversed so that R7 has a process slightly be-low its modal process while R5 happens to have a process slightly above its modal process, then the two stimuli may even have the same discriminal process, and there would be no possibility of a confident discrimination. Finally, if on some occasion R7 happens to have a process unusually low in its scale, while R5 has a process higher in the psychological scale, then the judgment would be made, perhaps even with confidence, that R5 is greater than R7, and the judgment would be recorded as incorrect. The discrimination is considered, then, as a function of the discriminal difference between the two processes that happen to be associated in the same judgment. By the discriminal difference is meant the linear separation on the psychological continuum between the two processes involved in any particular judgment. It may be designated S7.5 or more generally Ska. The discriminal difference is the same as the sense distance if we allow that the sense distance for two stimuli fluctuates from one occasion to the next.
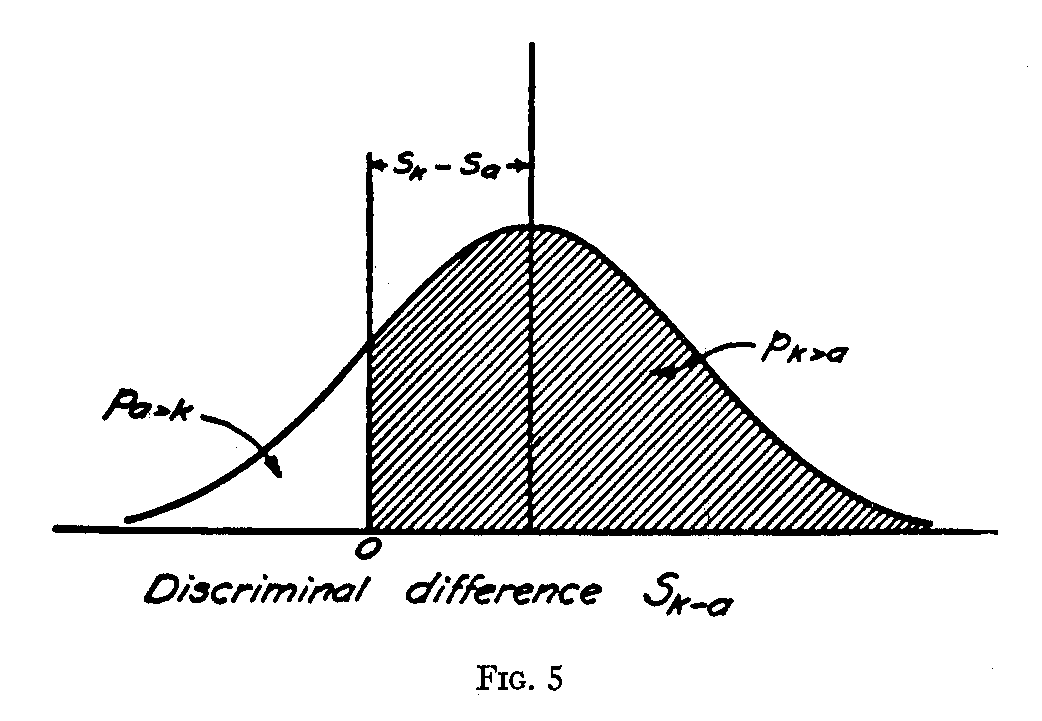
If in a long series of experimental judgments it were possible to isolate the two discriminal processes for every judgment and if the separation between these two processes for every judgment were recorded, one could tabulate them in the form of a frequency table of discriminal differences. These differences would of course be expressed in terms of some unit of measurement on the psychological continuum. Let the standard stimulus be A and the variable stimulus K. The mean
( 378) of the distribution of discriminal differences would be the mean or true difference (Sk— Sa), and its standard deviation would be
σka = √ (σk2 +σa2 )
on the assumption that deviations from the modal processes for the two stimuli are not correlated. This distribution is represented in Figure 5. The base line of this distribution represents discriminal differences in terms of any desired unit of measurement on the psychological continuum. The mean is (Sk— Sa) because that is the difference between the two modal processes. The origin represents a difference of zero. This would occur when the two stimuli happen to be associated with the same discriminal process, in which case there is no discrimination possible. The points to the right of the origin on the base line represent positive values for the differences Ska in which Rk has a process higher in the scale than Ra. Similarly, the points to the left of the origin represent negative values for the discriminal difference Ska in which Rk happens to have a process lower in the psychological scale than Ra. It should be recalled that Ska or Ska represents the sense distance between two stimuli on any particular occasion, whereas Sk Sa represents the mean sense distance for several hundred judgments, and it is in scale construction called the "true" sense distance or scale distance between the two stimuli.
For the present it will simplify analysis to assume that any discriminal difference, no matter how small, is directly reflected in the judgment. A correction may be inserted for this approximation by which a discriminal difference limen can be calculated, but this correction will not seriously alter the results. It may be assumed for the present that all positive discriminal differences, Ska, result in the judgment "Rk greater than Ra" and that all negative discriminal differences result in the judgment "Ra greater than Rk." If the two paired stimuli are presented N times, there will of course be observed N discriminal differences, and their expected distribution is represented in Figure 5. The shaded portion of that figure represents the expected proportion of judgments "Rk greater than Ra," and these judgments would be correct if K is higher than A. The unshaded portion of the surface represents the expected proportion of judgments "Ra greater than Rk." The proportion of correct judgments will of course increase if the two stimuli are chosen farther apart. Also, the proportion of correct judgments will increase if stimuli are chosen with smaller discriminal dispersions. If the shaded
( 379) area is greater than N/2, it represents correct judgments. If it is less than N/2, it represents the proportion of incorrect judgments.
A discriminal difference, Ska, is not necessarily a magnitude. It is a pair of processes, a pair of qualities. The only way in which numerical value is assigned to it is by placing each of these processes on a measured continuum by means of the frequency with which each of them is associated with the same stimulus. The difference between these two assigned linear values is the discriminal difference, Sk Sa. The scale distance, Sk— Sa, can be defined as the most common discriminal difference, Ska.
At this point we have arrived at a measure which can be experimentally verified. By the method of constant stimuli it is readily possible to ascertain the actual proportion of judgments "R7 greater than R5" for the two stimuli. This proportion is a function of four variables, namely, S7, S5, σ7, σ5,. If there are n stimuli in the stimulus series, there will be 2n unknowns to be evaluated, namely, n scale values for the modal discriminal processes and n scale values for the discriminal dispersions. If every stimulus is used in turn as a standard, the number of possible pairs of stimuli will be
T = (n (n 1))/2 .
Since there is an experimental proportion "a greater than b" for every possible pair of stimuli, it follows that there will be n(n — 1)/2 observation equations and 2n unknowns. One of the modal discriminal processes can be chosen as a datum or origin for the psychological scale, and one of the discriminal dispersions can be chosen as a unit of measurement for the construction of a psychological scale. This reduces the number of unknowns to (2n — 2) or 2(n — 1).
| Table I | ||||
|---|---|---|---|---|
| Number of stimuli in the series n |
Total number of unknowns (2(n-1) |
Number of observation equations, T = n(n-1)/2 |
||
| 1 | 0 | 0 | ||
| 2 | 2 | 1 | ||
| 3 | 4 | 3 | ||
| 4 | 6 | 6 | ||
| 5 | 8 | 10 | ||
| 6 | 10 | 15 | ||
| 7 | 12 | 21 | ||
| 8 | 14 | 28 | ||
| 9 | 16 | 36 | ||
| 10 | 18 | 45 | ||
(380)
Table 1 shows, for stimulus series of varying length from 1 to 10, the number of available observation equations and the total number of unknowns. When the stimulus series has less than four stimuli, the number of unknowns is greater than the number of observation equations, and the problem therefore cannot be solved. When there are four stimuli in the series, the number of observation equations exactly equals the total number of unknowns, and the problem can then be solved by simultaneous equations. When the stimulus series has more than four stimuli, there are more observation equations than there are unknowns, and the problem must then be solved by the method of least squares or by some other method of balancing errors of observation.
The fundamental psychophysical equation can then be stated in the following form:
Sk Sa = Xka√(σa2 + σk2 ) [2]
in which Sk and Sa are the two modal scale values on the psychological continuum for the two stimuli Rk and Ra.
Xka is the sigma value for the experimentally observed proportion of judgments "Rk greater than Ra." When these proportions are greater than .50, the stimulus Rk is higher in the psychological continuum than Ra.
σk = the discriminal dispersion of Rk on the psychological continuum.
σa = the discriminal dispersion of Ra on the psychological continuum.
The assumptions underlying this psychological equation are as follows:
(1) That every stimulus in the stimulus series is associated with a modal discriminal process with which the organism identifies the stimulus for a prescribed attribute.
(2) That the modal discriminal process for any given stimulus retains at least some of its identity even when the stimulus is combined with other stimuli into a single perceptual judgment.
(3) That the modal processes may be arranged in a linear psychological continuum in the same serial or rank order as the corresponding stimulus series.
(4) In addition to arranging the discriminal processes in rank or serial order, linear separations between them are assigned on the assumption that the discriminal dispersion for any stimulus is normal on the psychological continuum. This assumption is subject to experimental verification.
(5) That the discriminal deviations for the different stimuli are uncorrelated. This is a fairly safe assumption, but if they are correlated, the psycho-physical equation (2) becomes
Sk Sa = Ska√(σa2 + σa2 2 · rka · σk · σa) ,
in which case the numerical solution becomes unwieldy.
(6) That all positive discriminal differences Ska give the judgment "k > a," that all negative discriminal differences Ska give the judgment "k < a," and that discriminal differences of zero, Ska = 0, are equally distributed between "higher" and "lower" if only two judgments are allowed. This is a close approximation to truth, but a correction can be introduced in terms of a discriminal difference limen for judgments "equal" and "doubtful." This correction is left for a separate paper.
Experimental Procedure for Verifying Assumed Normality of Discriminal Dispersion
Assumption (4), that the discriminal dispersion for any stimulus is normal on the psychological continuum, may be experimentally tested by ascertaining whether the separation between any two modal processes (sense distance) remains constant no matter which of the stimuli is used as a base. Consider Rk as the base or standard for equation (2). Then the proportion of judgments k > a will be controlled by the relation
Sk Sa = Xka√(σk2 + σa2 ) [2]
Similarly for the proportion of judgments k > b
Sk Sb = Xkb√(σb2 + σk2 )
Subtracting,
Sb Sa = Xka√(σk2 + σa2 ) Xkb√(σk2 + σb2 ) [3]
If the same equation is written with Rl , Rm , Rn as standards, we have
Sb Sa = Xla√(σl2 + σa2 ) Xlb√(σl2 + σb2 )
= Xma√(σm2 + σa2 ) Xmb√(σm2 + σb2 )
= Xna√(σn2 + σa2 ) Xlb√(σn2 + σb2 )
If every separation, such as Sb — Sa, remains constant when determined by different stimuli, such as Rk, Rl, Rm, Rn, as standards, then internal consistency for the measurements has been demonstrated, and the validity of assumption (4) is thereby established. Such internal consistency depends on the nature of the assumed distribution of discriminal processes by which the psychological continuum is constructed.
The point of view that I am describing has many implications bearing on well-known psychophysical principles. One of the conclusions to which the present analysis leads is that Fechner's law and Weber's law are really independent and that it is consequently incorrect to speak of these two laws jointly as "the Weber-Fechner law." Another important conclusion relates to the well-known hypothesis that equally often noticed differences are equal. The present analysis shows that hypothesis is incorrect because it is possible for two differences to seem unequal on the average and yet be equally often discriminated. Other implications concern the limitations of the phi-gamma hypothesis in psychophysical experimentation and the distribution of judgments of equality. A few applications of the concept of discriminal dispersion are described below.
Fechner's Law
Fechner's law is usually phrased as follows: S=KlogR, in which S represents sensation intensity, which we have here called scale value. The notation R refers to stimulus intensity or magnitude. It will be noticed that in writing our psychophysical equation nothing has been said about stimulus magnitudes or intensities because of the fact that many stimulus series that are subjected to psychological measurement are not capable of quantitative measurement on their objective side. For example, the relative excellence of a series of handwriting specimens may be measured on a psychological continuum, but the corresponding physical "magnitudes" probably do not exist as a single variable. The physical handwriting specimens cannot be readily measured as to the stimulus variable "excellence."
Fechner's law can be applicable only to those stimulus series in which the attribute which is being judged can also be physically isolated. Then, if the discriminal separations of the psychological continuum are plotted against the physical stimulus attribute and if this plot is logarithmic, Fechner's law is verified.
In many cases there is no possibility of making sure that the physical variable really corresponds to the psychological one. For example, a series of circles can be arranged in a stimulus series in accordance with their diameters. The discriminal experiments may then be carried out with instructions to indicate which of two exposed circles is the larger without specifying further what is meant by larger. The circles would no doubt arrange them-selves in the same serial order in the psychological continuum as in the stimulus continuum, so that the two series would have exactly the same rank orders. Now, if we want to verify Fechner's law, we should plot the separations between the modal processes for the circles along the psychological continuum against the corresponding physical stimulus variable. Shall we plot diameters on the base line, or shall we plot areas? These two plans would arrange the stimulus series in the same rank order, but the relation between diameter and area is not linear. Both diameter and area would be physical variables covariant with the apparent bigness of the circles. Now, if Fechner's law is verified for one of these physical variables, it could not possibly be verified for the other because of the non-linear relation of diameter and area. If we should find experimentally that Fechner's law is satisfied by plotting the psychological continuum against the diameters, for example, that would not justify the conclusion that Fechner's law applies. We could artificially force Fechner's law everywhere by merely selecting that particular stimulus variable which does give a logarithmic relation with the psychological continuum. Fortunately, the law has been shown to hold true for many stimulus series in which there is hardly any possibility of an ambiguous stimulus variable, and its universality therefore commands our respect.
Weber's Law as Independent of Fechner's Law
In the present discussion Weber's law is interpreted broadly for the frequently observed relation between the stimulus magnitudes and the scale distances on the psychological continuum. I am not here limiting myself to those particular applications of the law by which it is restricted to sensory intensities. The law is not always verified for sensation intensities, but, on the other hand, I have found it applicable to some other stimulus series that are not sensory intensity magnitudes. The present discussion of Weber's law concerns the functional relation between stimulus magnitudes and psychological scale distances without implying that the law is limited to sensory stimulus intensities.
Weber's law and Fechner's law are often described together, and they are frequently called jointly "the Weber-Fechner law." The two laws are independent, so that either one of them may be applicable without the other being verified for a particular set of data. The two laws must be separately verified for any given set of data.
Weber's law is usually stated as follows: The just noticeable increase of a stimulus is a constant fraction of the stimulus. The term "just noticeable" is ambiguous, so that it is necessary to specify how often a stimulus increase must be correctly noted in order for the stimulus increase to be called "noticeable." This frequency is often placed arbitrarily at 75 per cent of the judgments when two judgments are allowed. Restating Weber's law with this provision so as to remove the ambiguity of the term "just noticeable," we have the following statement of the law: The stimulus increase which is correctly discriminated in 75 per cent of the attempts, when only two judgments "higher "and "lower," or their equivalents, are allowed, is a
( 384) constant fraction of the stimulus magnitude. With reference to Fechner's law there are two cases under which Weber's law may be verified. In Case 1 Fechner's law is postulated, and in Case 2 it is not postulated.
Case 1. Let the stimulus magnitude be designated Ra, and let it be in-creased to the magnitude, Rb, at which separation the two stimuli are correctly discriminated in 75 % of the attempts by the constant method and with two judgments allowed. At this separation between the two stimuli our psychophysical equation (2) takes the following form:
Sb Sa = Xab√(σa2 + σb2 )
which, when stated explicitly for the required proportion of 75 % judgments "b greater than a," becomes
SQ2 SQ=X, = 0.674. (4)
Z b' a
Weber's law states that any pair of stimuli, Ra and its increased magnitude Rb , corresponding to the two modal processes S. and Sb in the above equation, are such that the fraction Rb/Ra remains a constant no matter what the absolute magnitudes of the stimuli may be. It is clear from the above equation that the separation between the two stimuli which gives a result of 75 per cent correct judgments is a function not only of the two stimulus magnitudes and their corresponding modal processes but also of the discriminal dispersions for the two stimuli. Weber's law may be verified under Case 1 if an additional condition is satisfied, namely, that the discriminal dispersions are the same for all the stimuli. If the discriminal dispersions are not constant, then it is possible for Fechner's law to be applicable when Weber's is not. If the discriminal dispersions are equal for all the stimuli, then equation (4) may be written as follows:
and since the discriminal dispersion which is here assumed to be constant may be taken as a unit of measurement on the psychological continuum, we have
or
Sb Sa = √2 · 0.674 [6]
( 385)
This relation is obtained by condition (2) above. But Weber's law states a constant relation in terms of the stimuli. This transformation can be made by Fechner's law as follows:
Sa = K log Ra
Sb = K log Rb
Sb Sa = K [log Rb log Ra]
Sb Sa = K log Rb/Ra [7]
or simply
log Rb/Ra = constant
and hence
Rb/Ra = constant
thus verifying Weber's law. But in order to verify Weber's law under Case 1, it was necessary to make two assumptions, namely, that Fechner's law applies and also that the discriminal dispersions are constant. If stimuli were used of varying degrees of homogeneity or ambiguity, the discriminal dispersions would not be constant, and it would then be possible to discover that Fechner's law is applicable when Weber's law is not.
Case 2. It is possible for Weber's law to be applicable when Fechner's law is not verified and when the discriminal dispersions are not all equal. This is best illustrated by a short list of stimuli with hypothetical discriminal dispersions. For the purpose of this illustration we can assume any relation between S and R except the logarithmic relation of Fechner's law. Let us tabulate some paired values for S and R such that S = R2. This is clearly, then, a case in which Fechner's law does not apply. In Table 2 the first column identifies the six stimuli in the hypothetical series. Column R designates the stimulus magnitudes. Column S shows the scale values of the cor-
| Table II | ||||
|---|---|---|---|---|
| Stim. Series | R | S=R2 | σ | P(R+1) > R |
| 1 | 10.00 | 100 | 20.00 | .75 |
| 2 | 11.00 | 121 | 23.94 | .75 |
| 3 | 12.10 | 146 | 29.16 | .75 |
| 4 | 13.31 | 177 | 35.40 | .75 |
| 5 | 14.64 | 215 | 43.40 | .75 |
| 6 | 16.11 | 259 | 51.90 | .75 |
(386) -responding modal processes (sensation intensities). Column a shows a hypothetical series of discriminal dispersions. By means of the fundamental psychophysical equation [2] it can then be shown that the stimuli 1 and 2 are correctly discriminated in 75 % of the judgments, that stimuli 2 and 3 are correctly discriminated in 75 % of the judgments, and so on. Since the ratio of each stimulus magnitude to the next lower stimulus magnitude is always 1.10 in this table and since these successive pairs of stimuli are correctly differentiated in 75 % of the observations, we conclude that Weber's law has been verified by these hypothetical data. The only new factor that we have introduced is the plausible assumption that the discriminal dispersion may not be constant throughout the whole stimulus range. With an assumed variation in the discriminal dispersion we find that it is logically possible to have a set of data in which Weber's law is verified but in which Fechner's law is not verified. All that is necessary for the discriminal dispersion to vary from one stimulus to another is that the stimuli be unequal in the ambiguity or difficulty with which they are judged, and this surely must happen much more often than we suspect when the stimuli consists in such qualitative values as handwriting specimens or specimens of English composition. It is quite probable that the variation in discriminal dispersion is rather slight and perhaps negligible when the stimulus series is rather homogeneous. A good example of a homogeneous stimulus series is a set of cylinders for the lifted weight experiment in which size, color, texture, shape, and even temperature are ruled out of the experiment by keeping them constant. In such experiments it is probable that the discriminal dispersion stays constant.
Finally, if the discriminal dispersions can be assumed to be equal through-out the whole stimulus range, then Fechner's law and Weber's law become identical. The frequent association of these two laws as though they were always identical depends on the constancy of the discriminal dispersion. It may be expected, in psychophysical experiments with stimuli that are not experimentally kept constant in all but one stimulus variable, that one or two stimuli in the series are more difficult to judge than the rest. In such a case these one or two stimuli will have larger discriminal dispersions than the other stimuli, and the consistency of the psychological continuum is thereby disturbed if these variations are not accounted for in the derivation of the scale values.
( 387)
Equally Often Noticed Differences Are Not Necessarily Equal
It is usually assumed that equally often noticed differences are equal on the psychological continuum. They are rarely assumed to be equal on the stimulus continuum. It is, however, incorrect to assume that pairs of stimuli are equally distant on the psychological scale even though all the pairs are equally often discriminated. It is not even correct to say that stimulus differences seem equal, or that they are subjectively equal, just because the differences are equally often noticed. Two pairs of stimuli may be equally often discriminated, while one of the separations may on the average actually seem greater than the other.
Referring again to the psychophysical equation (2), the psychological or apparent separation between two stimuli Ra and Rb is expressed by the difference (Sb — Sa), measured on the psychological scale, which is a scale of appearances or impressions. The frequency with which the two stimuli can be discriminated is, however, a function of their respective discriminal dispersions as well as their modal discriminal processes. The separation between the modal processes can also be called the mean sense distance. Here again, if we can assume that the discriminal dispersions are constant, then it is correct to say that equally often noticed differences are psychologically equal, but that assumption should be tested before constructing a psycho-logical continuum or scale by means of this assumption.
A Possible Effect of Practice
It is probable that practice has the effect of reducing the discriminal dispersions and that this may account for the shifts in the proportions of correct judgments in psychophysical experiments. If two stimuli are presented to an unpracticed subject for whom these stimuli have relatively large discriminal dispersions, the denominator of equation (4) will be relatively
large while the numerator remains constant. Graphically, the situation can be represented in Figure 5 by increasing the standard deviation of that probability curve while the separation (Sk— Sa) remains constant. This produces a low proportion of correct judgments. With practice, the subject reduces the discriminal dispersions, and this might be represented in Figure 5 by reducing the standard deviation of that curve while the separation between the two modal processes remains constant. The effect is to increase the proportion of correct judgments. Naturally, stable results for the construction of a psychological scale depend on reaching such a practice level that the discriminal dispersions will remain prac-
( 388) -tically constant throughout the experiments. The interpretation of the psychophysical equation in connection with the effect of practice would be that two lights, for example, seem just about as bright to the practiced laboratory subject as to an unpracticed subject. Practice in psychophysical experimentation does not make one of the lights seem brighter or the other one weaker. The two lights retain their same general level of brightness except for sensory adaptation and contrast, which are momentary effects. But there is a practice effect in the capacity to discriminate between the two lights. This is determined by the discriminal dispersion or subjective observational error. Here again, equally often noticed differences are not necessarily equal subjectively or psychologically.
Experimental Test
The simplest experimental procedure for verifying the assumption that the discriminal dispersions are constant for any particular stimulus series is probably to arrange a table showing the proportion of judgments, Pa>b, for all the possible pairs of stimuli. If there are N stimuli, such a table will contain N(N — 1) entries if identical stimuli are not experimentally compared. From such a table the stimuli can readily be arranged in rank order. From the table of proportions of judgments, a corresponding table of sigma values can be prepared. One can then plot a graph for Xka against Xkb in which a and b are standards. If the discriminal dispersions are equal through the stimulus series, the graph should give a linear plot with a slope of unity. This may be demonstrated as follows:
If in the psychophysical equation
Sk — Sa = Xka ·√ (σk2 + σa2 ) [2]
we assume that the discriminal dispersions are equal, the equation becomes
Sk — Sa = Xka ·√2σ2
= Xka · σ ·√2[5]
and if we use the discriminal dispersion as a unit of measurement on the psychological scale, we have
Sk — Sa = Xka ·√2 [6]
By symmetry it follows that
Sk — Sb = Xkb ·√2 [7]
Subtracting and transposing,
Xka = Xkb + ( Sb Sa ) / √2 [8]
( 389)
This equation is in linear form, and if Xka is plotted against Xkb, we should have a linear plot. The slope should be unity and
Y-intercept = ( Sb Sa ) / √2 [9]
If the plot is linear, it proves that the assumed normal distribution of discriminal processes is correct. If the slope is unity, it proves that the discriminal dispersions are equal. It is left for a separate paper to apply this method to educational judgment scale data.