The Unit of Measurement in Education Scales
Louis L. Thurstone
University of Chicago, and Institute for Juvenile Research
The purpose of the present study is to show that the quartile deviation which is commonly, though incorrectly, called the probable error, or PE, is not valid as a unit of measurement for educational scales. Its defect consists in that it does not possess the one requirement of a unit of measurement, namely constancy. It fluctuates from one age to another. Hence the calculation of so called "PE values" for test items is of questionable value when these values are thought of as constituting a scale to represent several ages and grades. I hope to show that although the so-called PE scaling procedure is inadequate, the problem of scale construction can be solved so as to attain a valid unit of measurement for educational achievement.
In order to demonstrate the variation in the PE unit of measurement I shall apply an absolute method of scaling to the data for one of the best known educational scales. I have previously described this method of absolute scaling[2] and it will be used here on the data published by Trabue[3] for his language scales.
It should be stated at the outset that while I shall refer freely to Trabue's monograph with suggestions for improvements in scaling tech-
( 506) -nique, such references should not be taken as derogatory of Trabue's contribution. On the contrary, I have selected his monograph for this study because it is unusually complete in the data presented. His study was carried out with admirable completeness and he utilized the scaling technique developed by Thorndike and it is an improvement in this technique that I wish to illustrate by the application of an absolute scaling method to the data of Trabue's monograph.
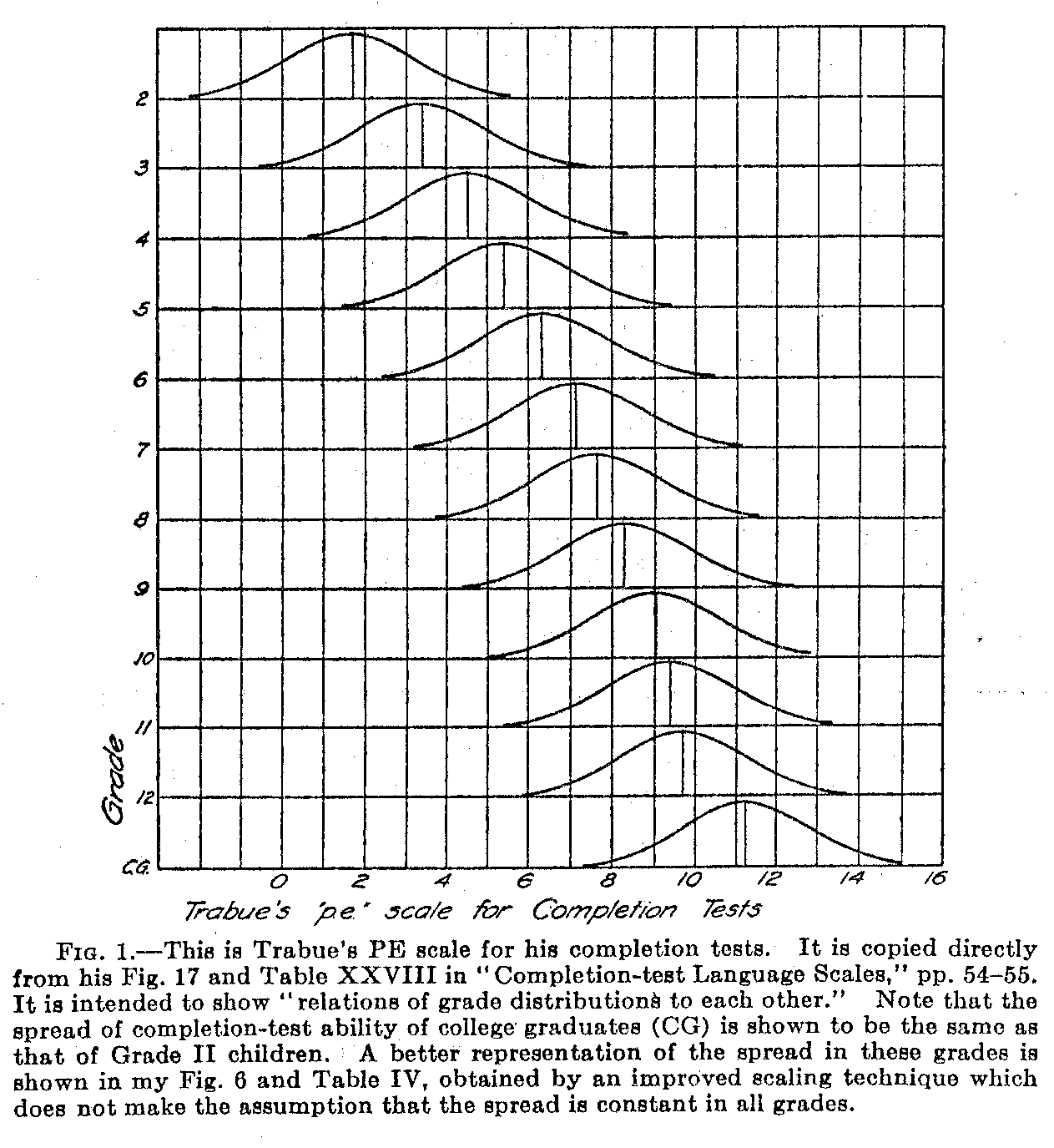
One of the principal final results of Trabue's calculations is represented in his Fig. 17 which is reproduced here as my Fig. 1. In reproducing the figure, I have separated the distributions of language ability
( 507) of the several grades on separate lines in order to facilitate analysis. Otherwise the figures are identical.
The interpretation of the diagram is as follows: On the upper line is a probability curve representing the frequency distribution of language ability to be expected in Grade II. The curve can be drawn to any convenient scale and the unit of measurement is the standard deviation of that surface or the quartile deviation (the so-called PE). The sentences in the language tests are given sigma values (or PE values) in accordance with the proportion of Grade II children who fill in the sentences correctly. The more difficult sentences will, then, be located toward the right of the mean while the easier sentences will be located toward the left of that origin.
On the second line of Fig. 1 is drawn another probability curve with the same standard deviation as the first. By this curve Trabue represents the distribution of language ability for Grade III children and it is located slightly to the right to represent the fact that the children move up in ability from the second to the third grade. Hence the mean of the Grade III distribution is higher than that of Grade II when the two surfaces are considered with reference to the same base line. On the base line of this surface one may also locate the sentences and it will be noticed that since the two surfaces overlap, many of the sentences will be common to both the Grade II and the Grade III distributions. The sigma value of each sentence may also he deter-mined for the Grade III distribution by the proportion of Grade III children who fill in each sentence correctly. Since we have two independent sigma values for each of the overlapping sentences, one for the Grade II children and one for the Grade III children, we are able to determine the lateral displacement between the two surfaces. It is by this means that one may determine the inter-grade interval, as it is called, which is the lateral or base line distance between the means of the two distributions.
At this point appears an assumption which is involved in the educational scaling technique developed by Thorndike, an assumption which is rarely stated explicitly and which will appear in our analysis to be not valid. The assumption is that when the distributions of abilities of several grades are plotted on a common base line or scale, their spreads or standard deviations will be equal. That assumption is implicit in the scaling technique of Thorndike but the assumption is not valid. In Trabue's monograph Fig. 17, with its supporting calculations (reproduced as my present Fig. 1), shows the spread in
( 508) language ability of Grade 11 children to be the same as that of college graduates. Now it seems hardly likely, even without the. application of an absolute scaling method, that the dispersion or spread in ability of Grade I1 children can be as great as that of college graduates because with the Grade II children there can be relatively little language ability to spread, whereas college graduates whose mean performance is of course very much higher on the scale have much more possibility for variation. However, this is a, priori reasoning which might be incorrect although it seems plausible. The absolute scaling method to which we can submit the data, answers this question on a factual basis. We shall then find that the PE unit commonly used in educational measurement is more than twice as large for the high school seniors as it is for Grade II children. It can also be shown that the inconsistencies in scale values which Trabue finds in his data are attributable to the fact that, his. unit of measurement the PE, is subject to gross variation in magnitude.
In order that the absolute scaling method may be clear, apart from its algebraic setting, let us consider first a hypothetical example in which the numerical relations have been simplified. Let Fig. 2 represent two grade distributions which refer to the same educational scale as a base line. The surfaces are drawn on two separate base lines for the sake of clarity. Let the distribution A represent the lower grade and B the upper grade. The mean performance of B is represented as higher in the scale than that of A which is to be expected since B is the higher grade. The lettered points on the base line of A may represent sentences, or other test items, which have been allocated along the base line in accordance with the proportion of right answers for group A. Let these sigma values take the numerical form shown in Table I. It will be seen that the sentences are arbitrarily spaced one sigma apart. Assume that the B distribution really has a spread twice that of group A as indicated in Fig. 2 and that the mean performance,,_ de B is equal to a performance of +3.Ov in the A-distribution. Find the sigma values .for the same sentences as determined by the performance of grade B are as represented in Table I.
Thorndike's scaling method consists in determining first the scale value of each test item for each grade separately with the mean of each grade as an origin. The difficulty of a test item for Grade V children, for example, is determined by the proportion of right answers to the test item in that grade. The difficulty is expressed as a deviation from the mean of that grade. «'hen a test item has been scaled in
( 509) several grades, the scale values so obtained will of course be different because of the fact that they are expressed as deviations from different grade means as origins. He then reduces all of these measures to a common origin in the construction of an educational scale by adding to each scale value the scale value of the mean of the grade. This procedure assumes that the distributions of abilities in the several grades are all of the same dispersion and that they differ only in lateral displacement along the scale. The procedure is well illustrated in Fig. 1 or in Trabue's Fig. 17.
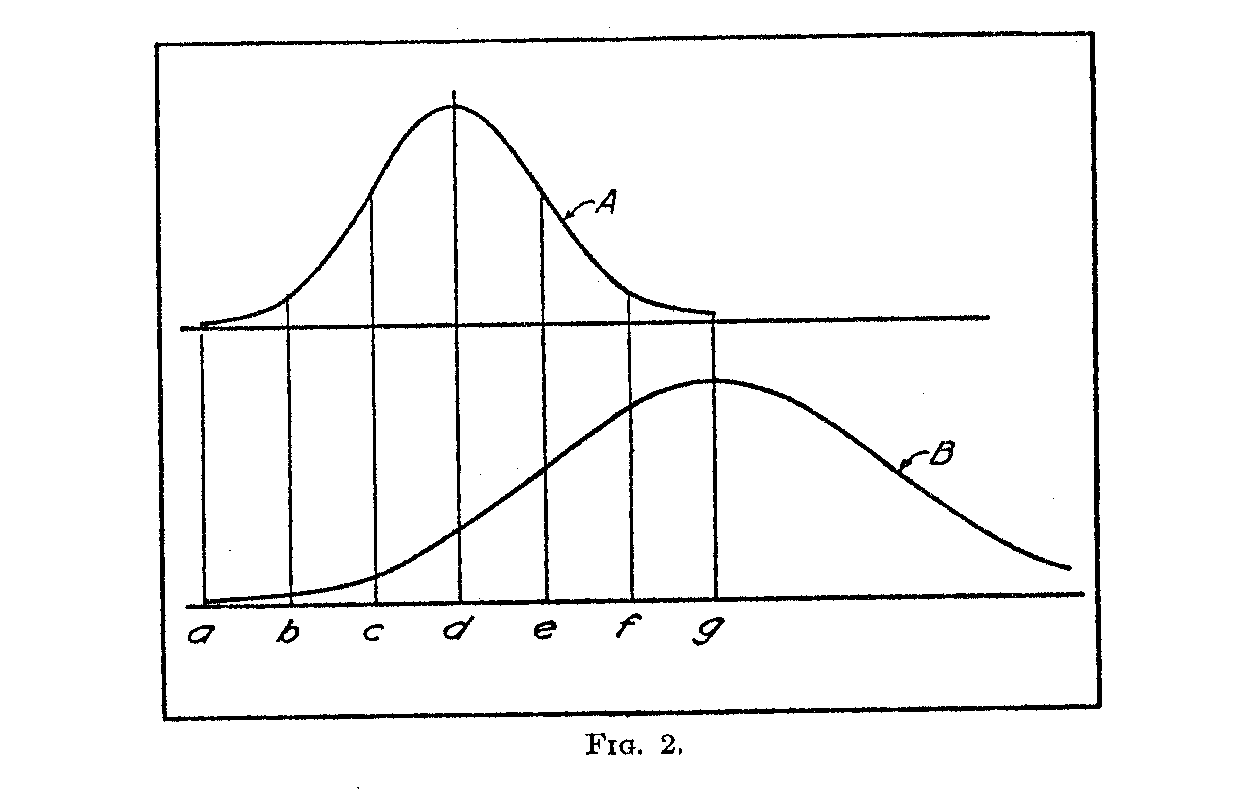
Referring to Fig. 2 it is clear that in order to reduce the overlapping sentences or test items to a common base line or scale it is necessary to make not one but two adjustments. One of these adjustments concerns the means of the several grade groups and this adjustment is made in the Thorndike scaling methods. The second adjustment which is not made by Thorndike concerns the variation in dispersion of the several groups when they are referred to a common scale.
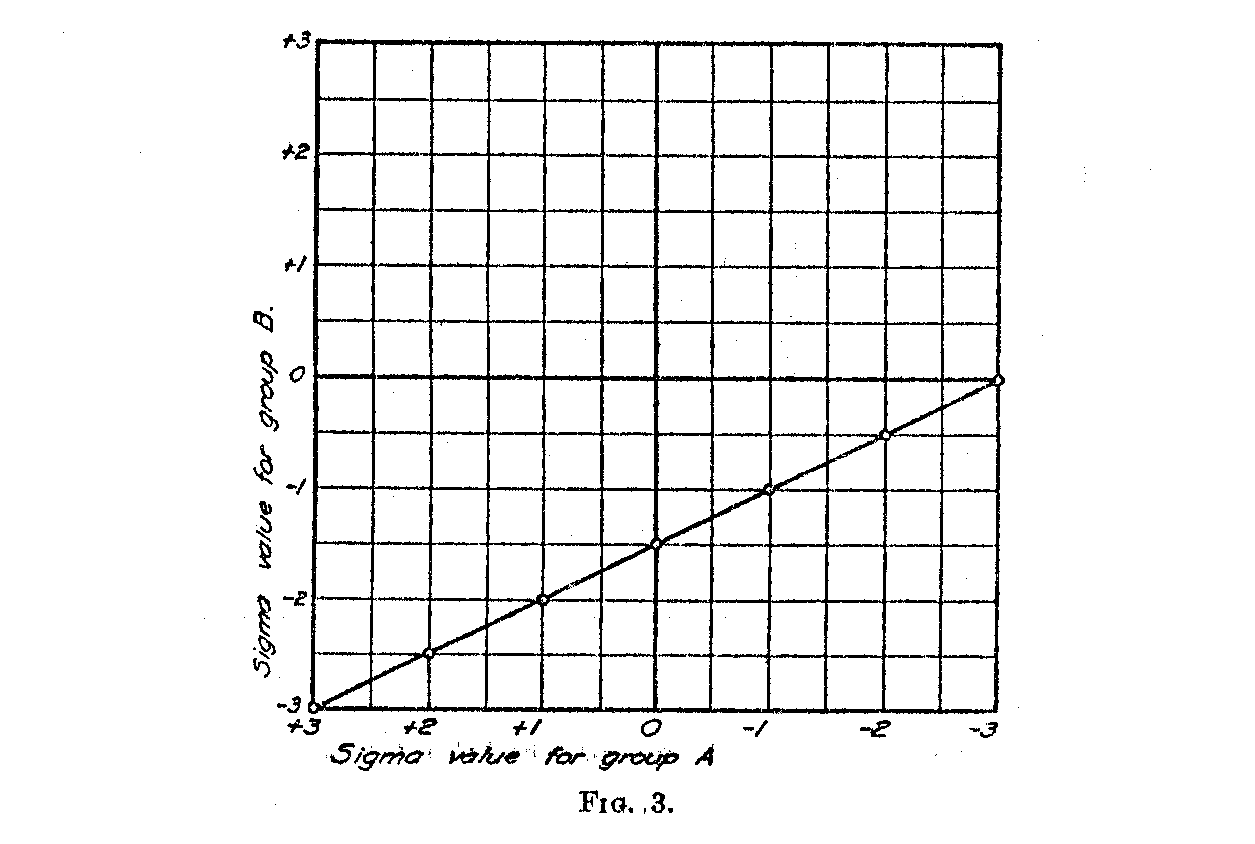
Table I represents for the fictitious and simplified example the scale values of the six test items in the two grades. If these paired scale values are plotted, the result is Fig. 3. The slope of this line is the ratio of the two dispersions, σA/σB. The slope of the line in Fig. 3 is 1/2 and this is consistent with the fact that in the hypothetical example the ratio σA/σB. = 1/2. We are dealing here with two differ-
( 510) -ent units of measurement, one for the A-distribution and another for the B-distribution. We may construct a common scale for the two distributions with either one of these two units but we can not guarantee consistent results by assuming that they are equal.
For the purpose of absolute scaling I have used the data of Trabue's Table XXXIV, page 62. The detail of the new method has been described in a previous article.[4] Tarbue's table was converted into a table of proportions and this in turn was re-stated in terms of sigma values for each grade separately.
The method consists in scaling each adjacent pair of grades. From the calculations one obtains two facts, the displacement of the two means, and the ratio of the two dispersions. In Table II an example of the calculations is reproduced for Grades VII and VIII. The first column shows the sentence number which corresponds to the numbering in Trabue's table. Columns 2 and 3 show the sigma values of the sentences for Grade VII, the tabulation having been separated into two columns for the positive and negative sigma values. Columns 4 and 5 show similarly the sigma values for the overlapping test sentences in Grade VIII. Only those sentences were here recorded which had proportions of right answers in both of these grades of more than .10
( 511) and less than .90. The elimination of the extreme proportions is made on account of the low reliability of these proportions. Strictly speaking, all of the sigma values should be weighted in accordance with the corresponding proportions but this has not been done on account of the considerable increase in arithmetical labor.
The last two columns in Table II give the squares of the sigma values in the previous columns. Table II shows a complete arrangement of the data for the absolute scaling of the two grades, VII and VIII, upon the same base line. The necessary summations are also given in Table II.
Table III shows a summary of all the necessary calculations for scaling Trabue's data for the grade combination VII and VIII. These calculations refer to equations (6) and (7) in my previous article. The mean of the lower grade, M7, and the standard deviation of that grade group, σ7, are obtained from similar calculations for the grade combination VI and VII. The unit of measurement adopted for the scaling is the standard deviation in language test ability for Grade II, and the origin for the scale is arbitrarily located at the mean performance of Grade II. It may be seen from Table III that
σ7 = 1,22081σ2
σ8 = 1,32713σ2
Hence these two grade groups do not have the same dispersion in language ability. The ratio between their dispersions is
σ7 / σ8 = .91988
and when it is considered that there is a progressive increase in dispersion from one grade to the next, this variation plays havoc with the educational scaling methods which assume that the dispersion is constant.
The steps in the absolute scaling method can be summarized briefly as follows:
1. Prepare a table showing the proportion of correct answers for each test item for each grade.
2. Convert this table into another table showing the sigma value of each test item for each grade or age group. This is done in the usual manner with the aid of a probability table. If quartile deviations (the so-called PE) are preferred, the table may be so arranged.
3. For each pair of adjacent grades construct a table like Table II. Since Trabue's data extend from Grade II to Grade XII inclusive,
( 512) there were in this study 10 tables similar to Table II. These tables represent respectively the grade combinations 2-3, 3-4, 4-5, and so on to 11-12.
4. Make the summations indicated in Table II.
5. Then arrange the calculations as indicated in Table III for each 1 grade combinations. In this study there were therefore 10 tables of calculations similar to Table III. The dispersion of one of the grade groups may be selected as a unit of measurement and its mean may be chosen for an origin. The standard deviation in completion test ability for Grade II was chosen as the unit of measurement for the whole scale and its mean performance was chosen as the origin, or zero, for the scale. It is clear that any other grade may be so used and the origin, or zero, may be placed at any other position, but it should be remembered that educational scales of this type do not have any real zero. The origin is necessarily in the nature of an arbitrary zero.
The calculations reproduced in Table III yield two important facts; namely, the scale value of the mean performance of Grade VIII and the standard deviation of performance in that grade. These are respectively
M8 = 3.07644
and
σ8 = 1.32713
The calculations should be carried to five decimal places even though the final figures may not be quoted to more than one or two decimals. This is a precaution which is advisable on account of the form of the algebraic expressions involved.
In addition, Table III also shows the equation of the line of relation for the scale values in the two grades. This equation, for Grades VII and VIII, is as follows:
X8 = .9198SX7 – .31722
in which X8 represents the sigma value of a test item for Grade VIII and X7 represents the sigma value for the same test item from Grade VII.
6. A graph is then drawn for each grade-combination like Fig. 4. This graph shows the relation between Xr and Xs and the numerical values are obtained directly from Table II. Since there are 36 sentences which give proportions of correct answers in both Grades VII
( 513) and VIII which are less than .90 and more than .10 there will be that many points shown in Pig. 4.
7. Plot the equation of the line of relation obtained in Table III on the graph of Fig. 4. If the arithmetical work is correct this line should be a good fit for the plotted points. Figure 4 shows a good fit and it thereby guarantees that at least no gross arithmetical errors have been made.
If the plot, in Fig. 4 should be distinctly non-linear, the present scaling method is not, applicable. Non-linearity here shows that the
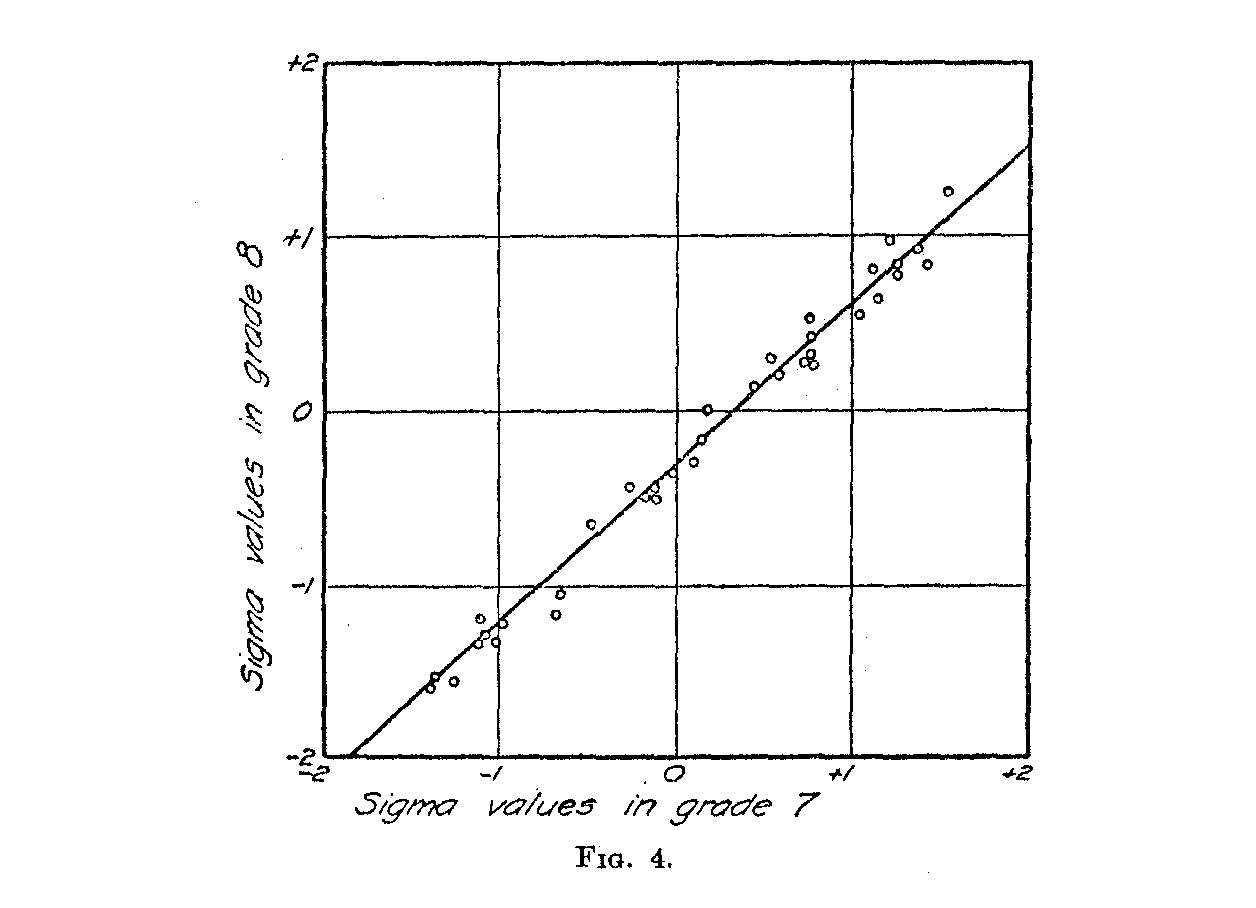
two distributions concerned cannot both be normal on the same scale. If the plot is linear, it proves that both distributions may be assumed to be normal on the same scale or base line. The slope of the line shows the ratio of the two dispersions and the intercepts show the lateral displacement of the two means when both distributions are plotted on the same scale
The results for all the 10 grade combinations in Trabue's data are shown in Table IV. Note that the dispersion for Grade VIII is about 33 per cent larger than that of Grade II and that the dispersion of Grade XII is more than twice as large as that of Grade II. According to the customary methods of constructing educational scales these
( 514) dispersions are assumed to be equal. In order to have a scale with positive scale values for all the sentences, the origin was placed at – 3σ2 for the column of scale values in Table IV.
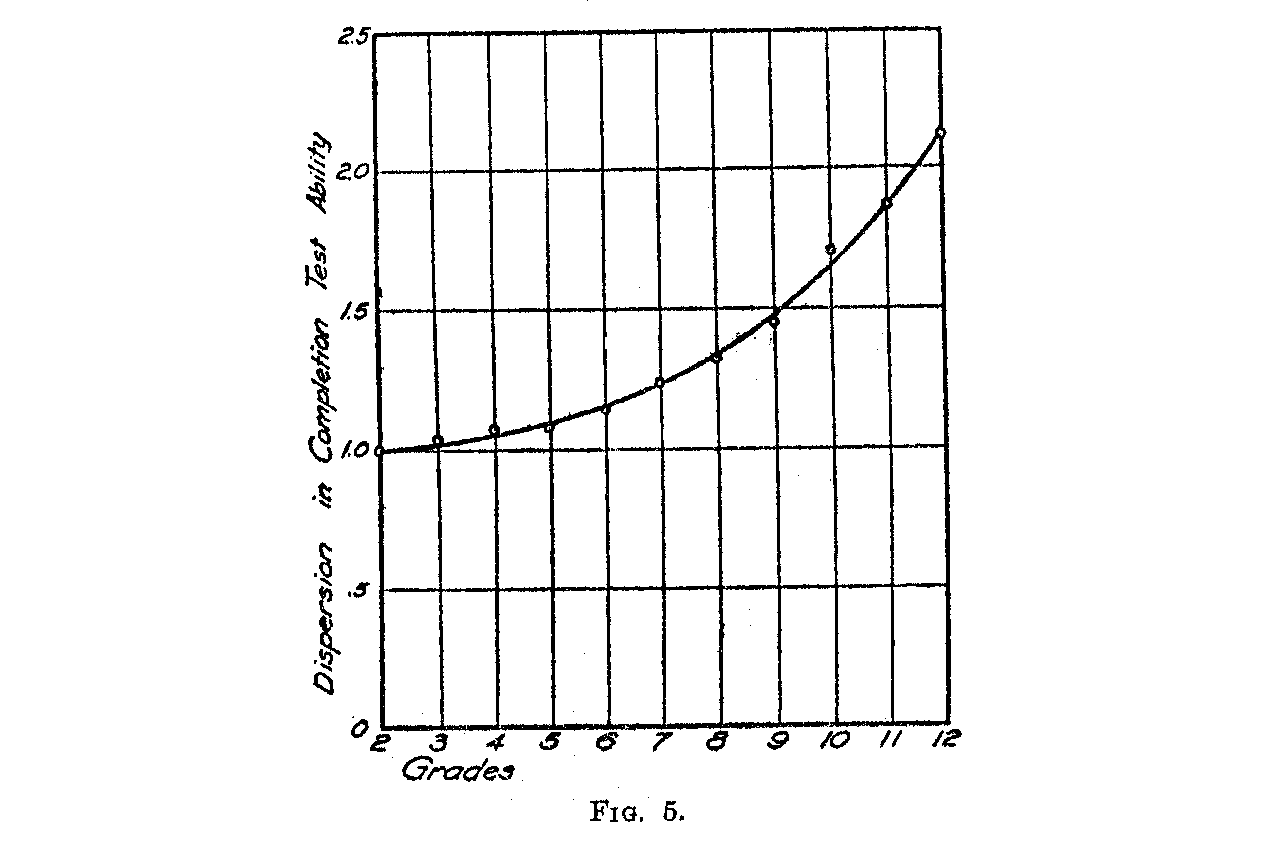
The rate at which dispersion in the sentence completion test increases through the grades is shown in Fig. 5. Note that the rate of increase is positive. The conclusion is inevitable that children tend to become more unlike in the ability measured by the Trabue tests as they progress through the grades. Figure 5 is obtained from Table IV.
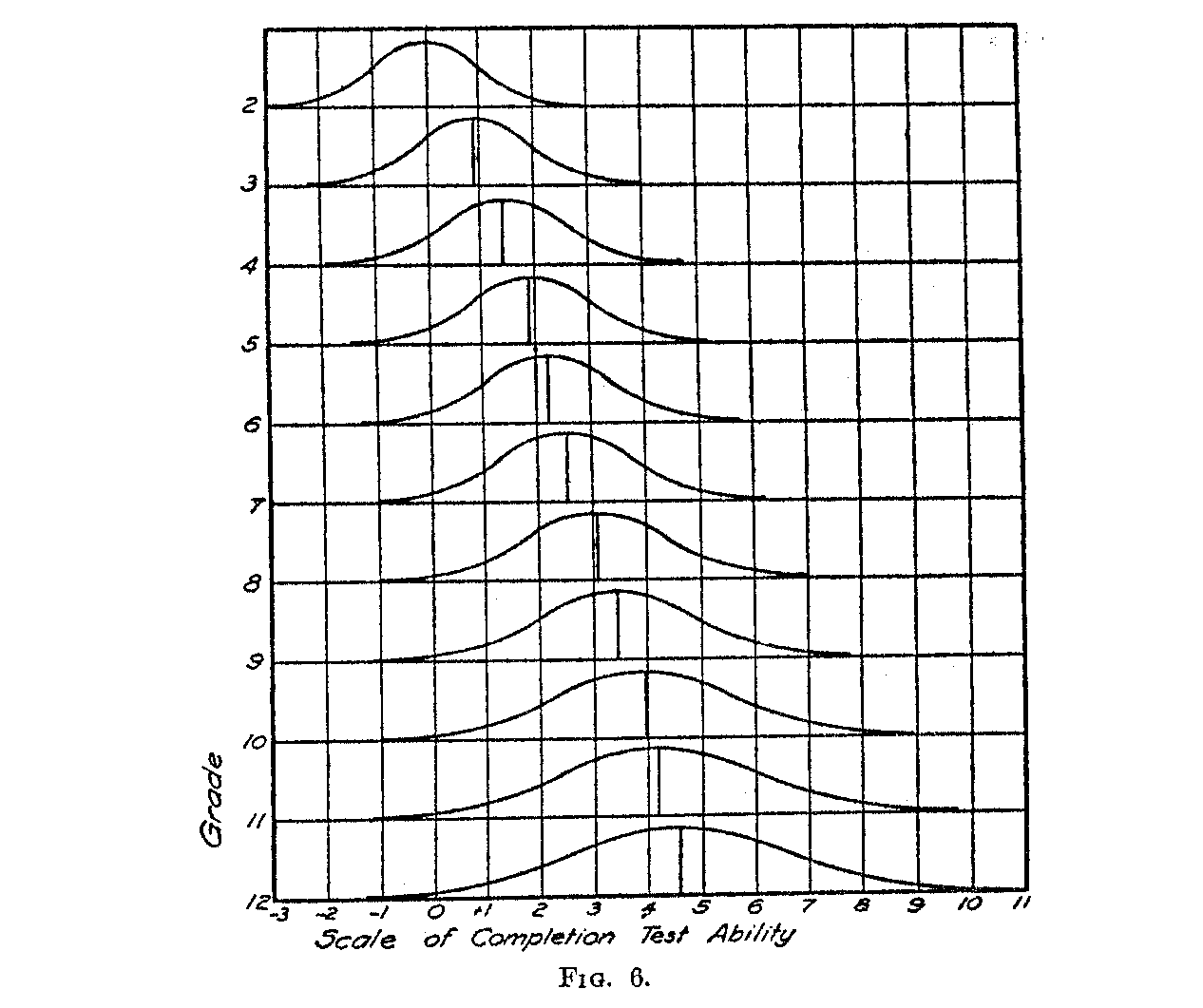
We are now ready to draw a graph showing the distributions of completion test abilities in all of the grades upon the same scale. This has been done in Fig. 6 the data for which are obtained from Table IV. Note that these distributions do not look like those of Fig. 1 which were copied directly from Trabue's Fig. 17 and Table XXVIII.
When we have ascertained the mean and standard deviation of each grade-group, referred to a common base line or scale, we may allocate each test item on that scale. Trabue has done this with consider-able completeness but he says of his tabulation: "It will be noticed in Table XXIX that there is a tendency for each sentence to have a higher location in the higher grades than it has in the lower grades." It is more than a "tendency." In his more complete Table XXXVI, all but one of the 56 sentences jump in scale value about three or four
( 515) PE units and some as much as 5.5 PE units which is more than half the range of the whole scale. He attempts an explanation for it which is probably not correct. The reason is that the unit by which the scaling is accomplished is itself variable. It increases with age, as has been shown, and it should therefore not be expected that the scale values of the items should remain constant when determined independently for the different grades.
In his Table XXXVI, page 64, sentence 1, for example, is given a "location above zero" of 1.15 when determined by the data for Grade II, and 6.65 when determined by Grade XII. This conspicuous drift in the data is avoided by the scaling method here proposed.
Our analysis corresponding to Trabue's Table XXXVI is as follows: For every grade, we have calculated a mean, M, and a dispersion, v, and these are listed in Table IV. The scale value of any particular sentence is then determined by the relation
Sk = Mg + Xk σg (1)
( 516)
in which
Sk = difficulty or scale value of sentence k.
Mg = grade mean of grade g.
Xk = sigma value of observed proportion of correct answers
to sentence k in grade g.
σg = dispersion of ability in grade g.
The application of the above equation may be seen in the following example: Referring to Trabue's Table XXXIV, page 62, we find that 1008 children in Grade VI filled in sentence 20 correctly. Since Trabue gives 1158 as the perfect score, he calculates the proportion of correct answers to be equivalent to about 87 per cent. With these data given, we determine the sigma value of this question to be -1.126 σ6.
The values of M6 and σ6 are obtained from our Table IV and we then have
S = 5.27918 – 1.126 x 1.13879 = 3.9537
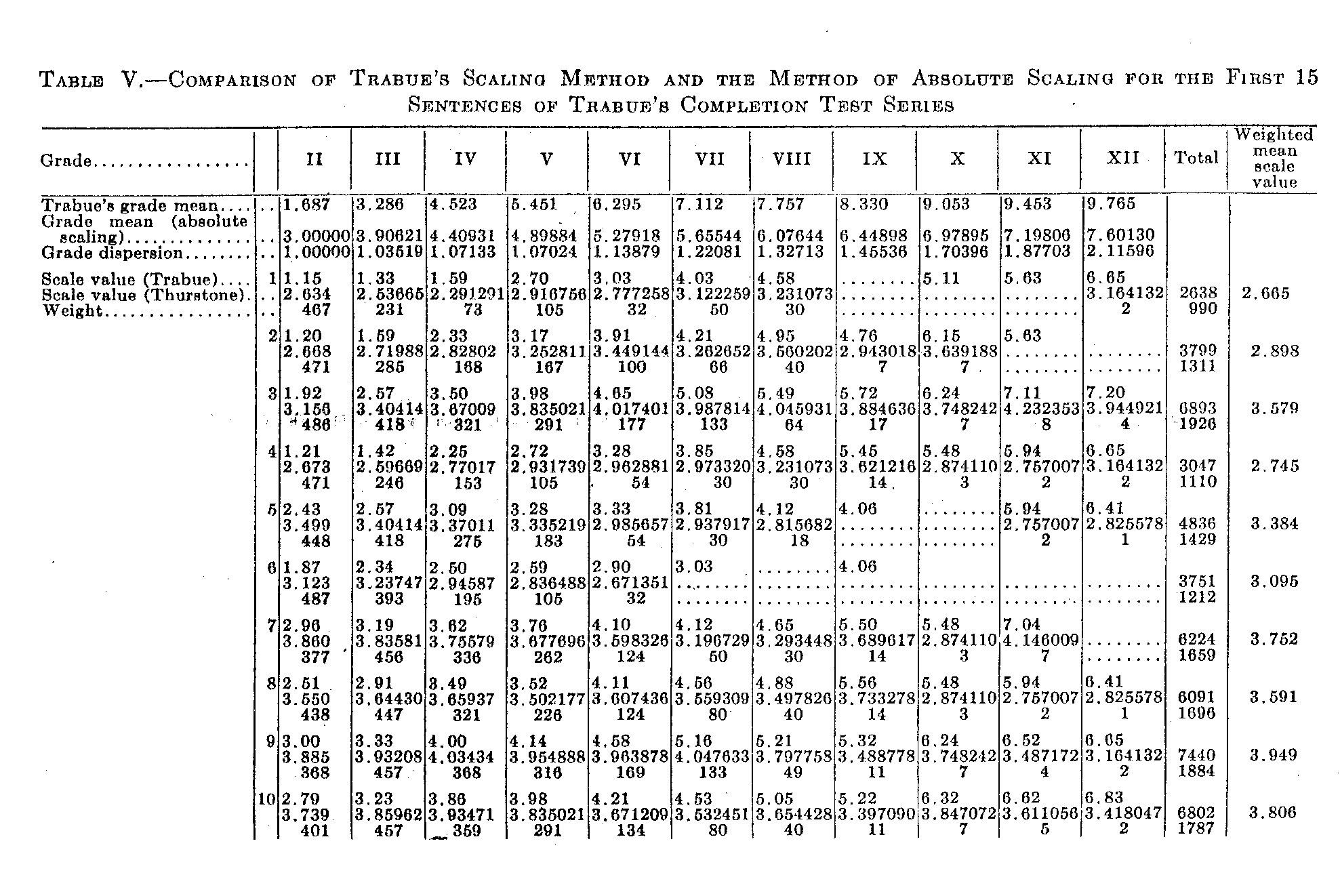
This is, then, the scale value of sentence 20 as. determined by the performance of Grade VI children. In a similar manner we have calculated the scale value of each of the 56 sentences for each of the twelve grades. The results are shown for the first 15 sentences in Table V. The rest of the table can be readily reproduced from the raw data of Trabue's Table XXXIV and our Table IV.
Table V has been arranged so that the two scaling methods may be directly compared. At the top of the table are given three facts for each column namely (1):Trabue's grade mean, (2) our grade mean, and (3) our measure of dispersion for each grade. The sentence numbers are indicated in the first left-hand column. The first line of each group of three entries represents Trabue's scale value, obtained from his Table XXXVI. The second entry is our scale value. In the third line is recorded the weight that is to be assigned to our scale value.
The comparison may be made horizontally. For example, Trabue calculated the scale values for sentence 10 in the different grades as follows (see my Table V or his Table XXXVI):
|
Scale Values for Sentence No. 10 |
||||||||||||
| Grades | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Trabue | 2.79 | 3.23 | 3.86 | 3.98 | 4.21 | 4.53 | 5.05 | 5.22 | 6.32 | 6.62 | 6.83 | |
| Absolute Scaling | 3.74 | 6.86 | 3.93 | 3.84 | 3.67 | 3.53 | 3.65 | 4.00 | 3.85 | 3.61 | 3.42 | |
(517) Note that the Trabue scale values range from 2.79 to 6.83 PE units while our scale values, determined by the method of absolute scaling, hover about 3.8 as a mean.
Similar comparisons may be made for other sentences in Table V. The first line for each sentence shows the Trabue scale values for that sentence in the different grades. The second line for each sentence shows our scale values, determined by the method of absolute scaling. Note the constant increase in Trabue's scale value for each sentence from grade to grade and the smaller chance fluctuations in our scale values.
On the basis of a tabulation similar to Table V for all of the 56 questions we have ascertained the number of sentences for which the last entry is higher than the first. I find that in 22 sentences the last entry happens to be higher than the first, while in 34 they happen to be lower than the first. The fluctuation in scale values in our data are due primarily to variable or chance errors which are in comparison small.
Before a mean scale value can be calculated for each sentence, it is
necessary to note that the reliabilities of the scale values for any particular
sentence are not the same in the several grades. The scale values recorded in
Table V must be weighted before a mean scale value for each sentence can be
calculated. There are three factors that determine the reliability of a scale
value calculated from equation (1). These are (1) the number of cases on which
the original proportion of correct answers is calculated, (2) the actual
proportion of correct answers, and (3) the dispersion of the grade-group. The
reliability of a proportion of a normal probability surface is as follows:[5]
σp = ( σ/√n ). (√(pq/Z2)
Since the weight should be inversely proportional to the square of the reliability, we have
w = (n/σ2) . (Z2 / pq)
The value of p is known from the raw data, and also the number of cases, n. The factor q = 1 – p. The value of Z is ascertained in a probability table. In the present study the factor Z2 / pq was calculated for values of p which were recorded to two decimals only. The
( 517) value of σ is found in Table IV. The weights so determined constitute the third entry of each set in Table V.
By means of the weights we are now able to calculate the weighted mean scale
value for each of the 56 sentences. The weighted mean scale value for each
sentence is
mk = wk.1Sk.1 + wk.2Sk.2 + wk.3Sk.3 . . . + wk.12Sk.12
wk.1 + wk.2 + wk.3 + . . . wk.4
in which
mk = weighted mean scale value of sentence k.
wk.1 , wk.2 , wk.3 , etc. = weight assigned by equation (2) to sentence k in Grades I, II, III, etc., respectively.
Sk.1 + Sk.2 + Sk.3 = scale value assigned by equation (1) to sentence k in Grades I, II, IH, etc., respectively.
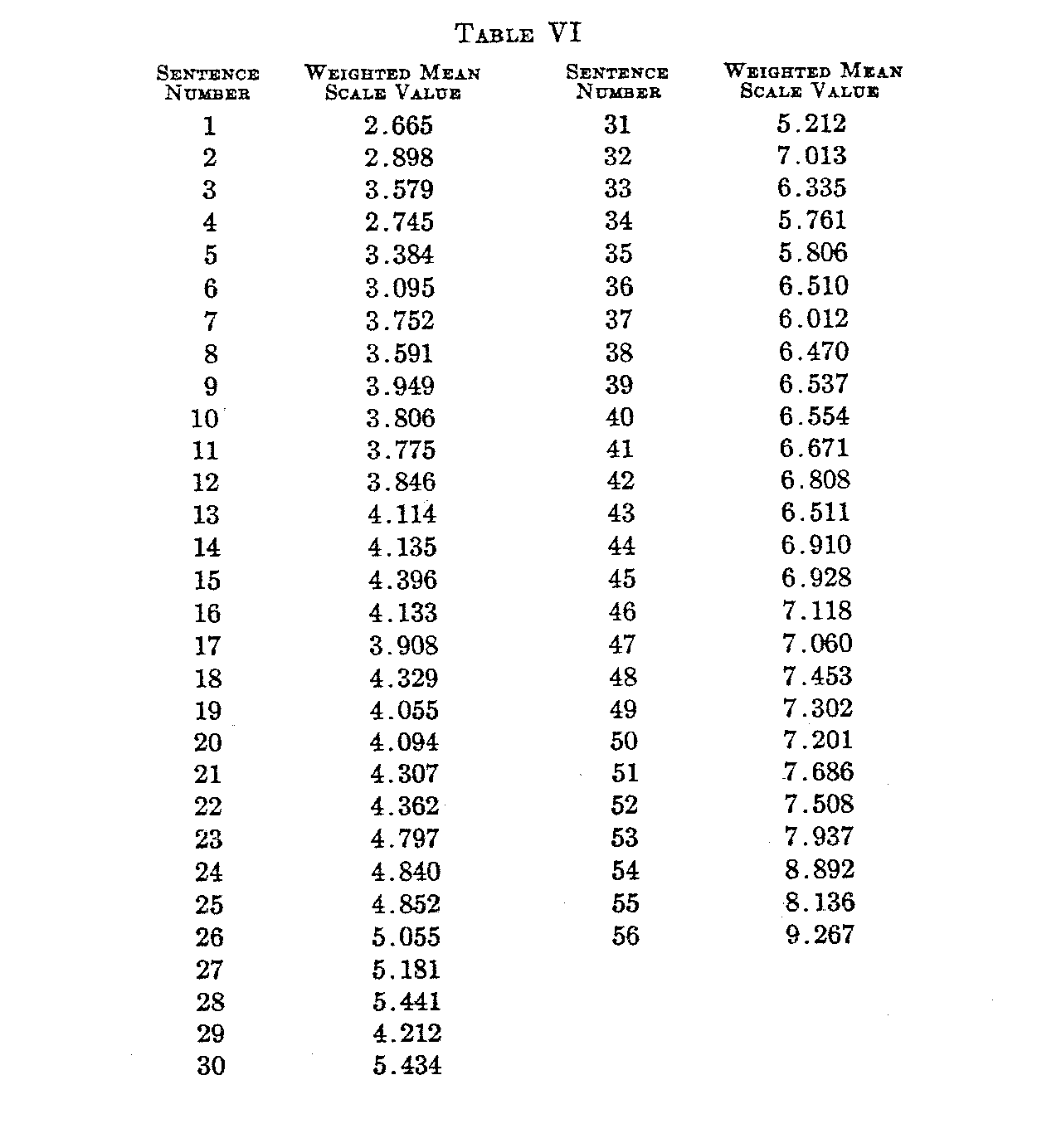
Table VI shows the weighted scale value for each of Trabue's 56 sentences. In this table the origin is placed at -3 σ2 a, in which σ2 is the dispersion of ability in Grade II and σ2 is itself the unit of measurement.
SUMMARY
1. The main purposes of this study have been (1) to show that the quartile deviation or the so-called PE is entirely unsuited as a unit in educational scale construction because of the fact that it is subject to considerable variation among the different grades and ages, and also (2) to offer a solution to the problem of scale construction. The variation in the PE unit has been shown on the data of Trabue for sentence completion tests because his study is one of the best known and best prepared scaling projects of the type here discussed.
2. It has also been shown that inconsistencies which Trabue discusses in his own scale values disappear by the application of an absolute scaling method which takes into account the fact that dispersion is itself a variable among different grade and age groups. The detailed description of this absolute scaling method has not been repeated here because it has previously been described in another article, but examples of each type of calculation involved have been reproduced here to facilitate the application of the method to other educational scaling data.
3. The method of absolute scaling enables us to ascertain whether two, age or grade distributions can be represented as normal surfaces on the same base line even though the original raw-score distributions be skewed. The test consists in the linearity of the plot illustrated in Fig. 4.
( 519)
4. The method of absolute scaling is independent of the number of easy or difficult items in the scale. The fact that the test items are bunched close together in difficulty or spread apart on the scale has no effect on the scaling of the several age or grade groups. The fact that one happens to use questions that are relatively hard or easy for a grade group has no effect on the inter-grade interval or the inter-age interval in the absolute sealing method here described unless the data are so badly bunched as to affect the scaling on account of unreliability of extreme proportions.
5. The method of absolute scaling here used is based on successive comparisons of adjacent age or grade-groups, such as II–III, III–IV, IV–V, etc. For the present, only those test items have been included which gave proportions of correct responses between 10 per cent and 90 per cent in both of the adjacent groups and they have all been given equal weight. A more complete absolute scaling procedure will be described in a separate article in which all of the test items are included with weighting in accordance with the reliability of the proportion of correct answers for each test question. Each grade mean and grade dispersion will then be ascertained by two normal equations. In the complete procedure, the scale might be constructed by comparing all grades simultaneously instead of adjacent pairs of grades in succession. This procedure would be laborious for Trabue's data in that it would require the solution of 20 normal equations with as many unknowns, namely, 10 scale values for the grade means and 10 grade dispersions. The labor of such a solution is almost prohibitive. Hence the compromise by which adjacent grade groups are scaled in succession to cover, stepwise, the whole grade-range.
The central idea involved in the method of absolute scaling is to provide for the varying dispersion of ability in successive ages and grades. Thorndike's scaling method makes the tacit assumption that the dispersion is constant, an assumption which has been demonstrated to be not valid. The method of absolute scaling may be considered as an improvement on Thorndike's scaling in two regards, namely, (1) by providing for the varying dispersion, and (2) by providing a rational procedure by which all of the data may be adequately taken into account. We have called the method absolute, not in the sense of measurement from an absolute origin but in the sense that the scale is independent of the unit selected for the raw scores and of the shape of the distribution of raw scores.
( 520)
(521)

(522)
( 523)

( 524)