Equally Often Noticed Differences
L. L. Thurstone
University of Chicago and Institute for Juvenile Research
Quality scales such as Thorndike's scales for handwriting and for children's drawings are constructed on the principle that equally often noticed differences are equal. It is the object of this paper to examine this principle of scale construction and to show that the principle is valid only when the stimuli or specimens are uniform in the degree of ambiguity or dispersion of excellence that is perceived in them.
The principle that equally often noticed differences are equal is a psychological commonplace. Of course the principle does not say anything whatever about the physical differences between the stimuli. That is a totally different matter. Some stimuli are of such a character that a physical scale can be postulated, parallel to the psycho-logical scale. An example is the lifted weight series. The weights may be allocated on a physical scale in grams and the same weights may be allocated on a psychological scale in accordance with the principle that equally often noticed differences are equal. The construction of an educational quality scale is not ordinarily concerned with the physical scale.
For some kinds of stimuli there exists no physical scale that can be at all readily defined or measured. The excellence of handwriting or of freehand drawing is an example in which the specimens may be allocated on a psychological scale of excellence, as perceived, but for which it is at least difficult to define a parallel physical scale. However, it is possible to construct a quality scale without giving any consideration to the possibility of a parallel physical scale. It is an interesting inquiry to search for the physical measurements that may parallel the psychological measurements but the present analysis is concerned
( 290) only with the psychological scale which is constructed on the basis of relative frequency of discrimination between the specimens.
When we say that equally often noticed differences are psychologically equal, it sounds so obvious that we are tempted to regard the assertion as a psychological axiom. But the matter is far from being
so simple. In fact, equally often noticed differences are not always equal, not even psychologically. The matter can be made clear by considering a simple case.
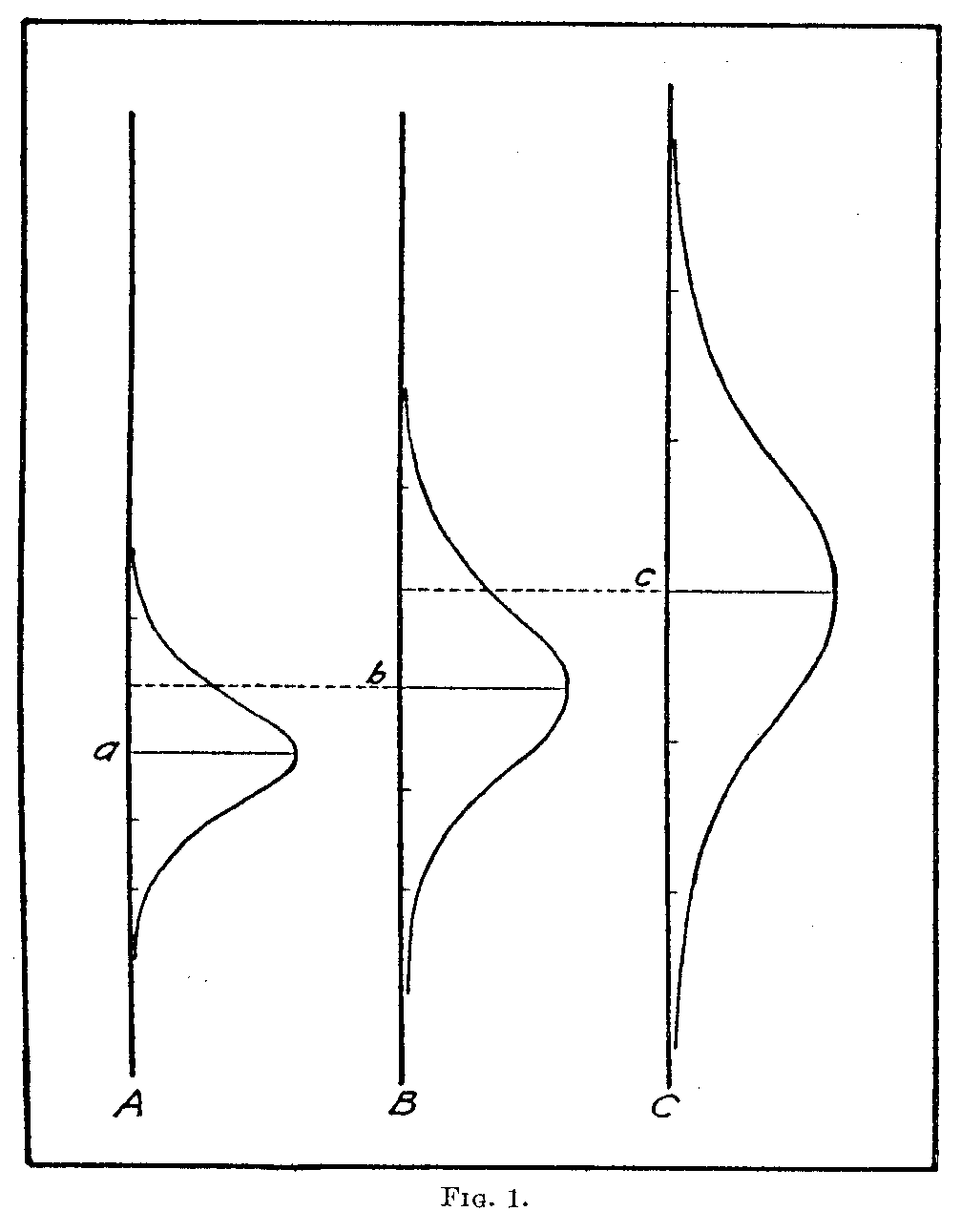
In Fig. 1 let the vertical dimension represent a psychological continuum such as Thorndike's handwriting scale. Let a represent the scale value of one of the handwriting specimens A. The small probability curve may represent the fluctuation in scale value as
( 291) perceived by several hundred judges. Let the spread or dispersion of this distribution be designated Sa. Let b and c represent the scale values of two other handwriting specimens B and C. Suppose that specimen C is more ambiguous to judge for degree of excellence than B, and that B is more ambiguous than A. This means, merely, that the several hundred judges differ considerably in the degree of excellence that they see in specimen C and that they agree more closely as to the excellence they perceive in B while specimen A shows the best agreement with the smallest dispersion in perceived excellence. In Fig. 1 the three distributions are so drawn that
σa = 2/3/σb
and
σb = 2/3σc
The scale value b is the mean degree of perceived excellence in specimen B and it is represented at the level +1σ on the distribution for specimen A. In exactly the same proportional arrangement, the mean perceived excellence of C, its scale value, is located at the level of +1σ on the distribution for specimen B.
It is readily seen in Fig. 1 that the overlapping or confusion between A and B is the same as that between B and C. Hence we should expect the same proportion of judgments "B better than A" as of judgments "C better than B." By the application of the law of comparative judgment[2] to the present case, the proportion
pB>A = pC>A=.71
We have here a situation in which the two scale differences (B — A) and (C — B) which are clearly unequal on the psychological scale are nevertheless equally often noticed. In fact
(C — B) = 2/3(B— A).
'Without considering the validity of the fundamental psychophysical equation by which the exact proportion .71 is determined, it is clear from inspection of Fig. 1 that the proportion of judgments "C better than B" must be equal to the proportion "B better than A " because the relations between A and B are duplicated in the relations between B and C.
We conclude, therefore, that equally often noticed differences are equal only when the discriminal dispersions of the specimens are equal.[3]
( 292)
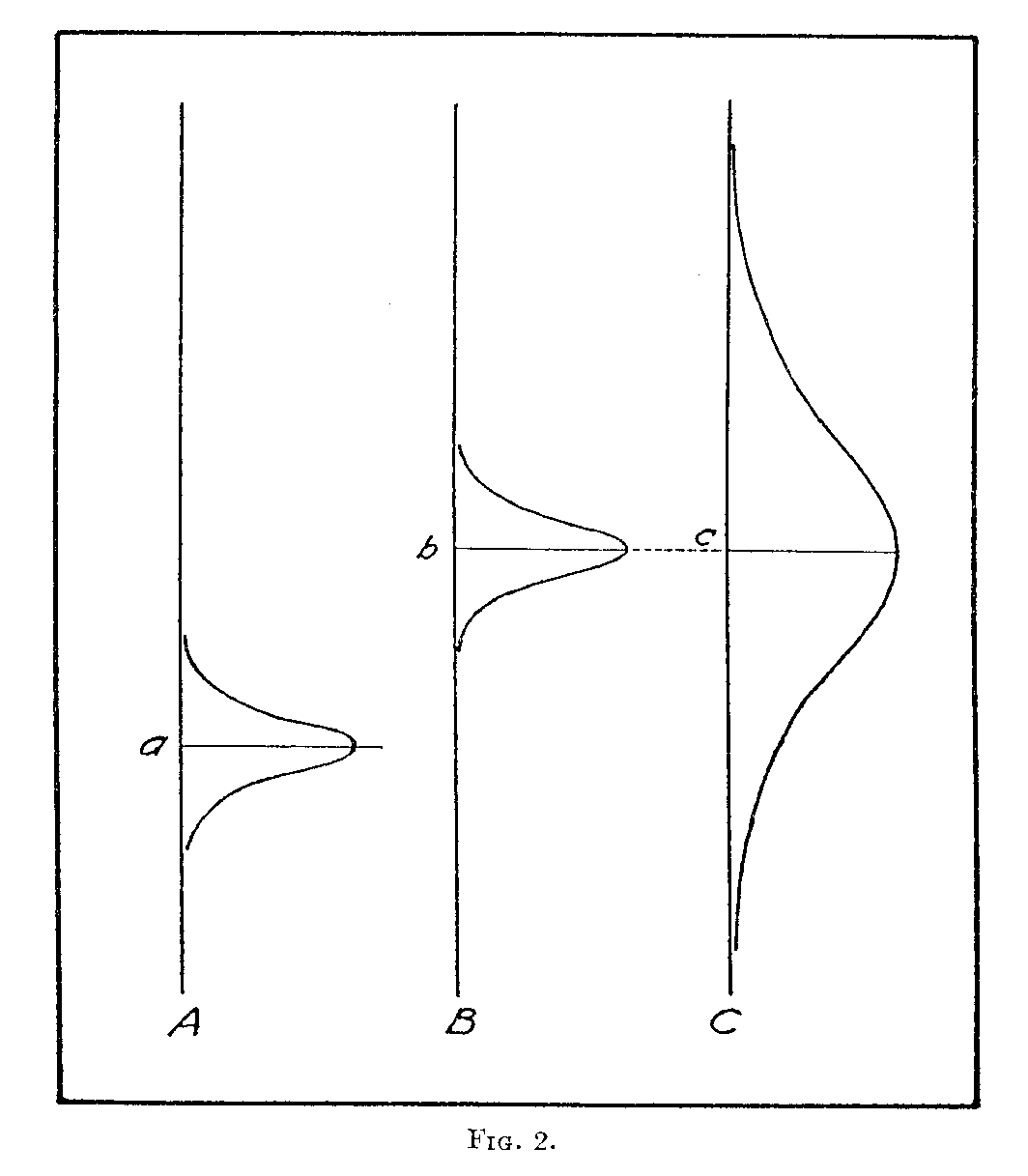
Figure 2 has been drawn to show the converse statement, namely, that equal psychological separations are not necessarily equally often noticed. Let Fig. 2 represent three specimens, A, B, C. Let the specimens A and B be easily perceived with very little ambiguity while specimen C is difficult to evaluate. Specimen C is therefore shown with a large dispersion as compared with the dispersions of A and B.
Since B and C have the same scale value it follows of course that
(B — A) = (C — A)
Now consider what will happen when the judges are asked to compare specimens A and B. Since the lowest excellence that any judge sees in B is approximately equal to the highest excellence that any judge sees in A, we should expect a very high proportion of judgments "B better than A," perhaps 90 or 95 per cent.
The judges are then asked to compare B and C. Half of them see specimen B as more excellent than the scale value b, and half of them see specimen C as more excellent than the scale value c. If we assume for the sake of simplicity that the variations in perceived excellence of specimens A, B, C, are uncorrelated, it is evident that the percentage of judgments "B better than C" will be .50. Hence these two specimens B and C are declared to have the same scale value and they are so indicated in Fig. 2.
Now let the judges compare specimens A and C. Notice that there is considerable overlapping in judgments of excellence for A and C. For example, a considerable proportion of the degrees of perceived excellence for C is below the average judgment for A. Hence we shall expect to find a proportion of judgments "C better than A" about 70 or 80 per cent but certainly not 90 or 95 per cent.
Since B = C it follows that
B—A=C—A
and that the difference (B — A) should be as often discriminated as (C — A) but we have seen in Fig. 2 that if the stimuli or specimens are unequal in relative degree of ambiguity the two equal differences (B — A) and (C — A) will not be equally often noticed. We conclude therefore that equal psychological differences are equally often noticed only when the discriminal dispersions of the specimens are equal.
If the discriminal dispersions can be assumed to be constant for all of the specimens in a series or scale, then the principle that equally
(293) often noticed differences are equal is valid, but it is hardly likely that the assumption is always justified. In psychophysical experimentation with lifted weights, for example, it is probably safe to assume that the ambiguity is constant because the weight cylinders are all alike, in appearance, and they are even kept at the same temperature by careful experimenters so as to avoid thermal cues caused by having the sub-
-ject handle the standard weight-cylinder more frequently than the comparison-cylinders. But it is hardly likely that specimens of English composition, for example, are sufficiently homogeneous in ambiguity of excellence to justify the assumption that equally often noticed differences are equal. Certainly this is an assumption to be experimentally verified in each case. Equally often noticed differences are not necessarily equal, not even subjectively or psychologically.