The Mental Age Concept
L. L. Thurstone
University of Chicago
It is the purpose of this article to show that the mental age concept is a failure in that it leads to ambiguities and inconsistencies. In discussing the logic of the mental age concept, we shall have occasion to describe two definitions of mental age, both of which are in use and both of which lead to the same ambiguities.
The two definitions of mental age which are either stated or implied in current mental test work are as follows:
1. The mental age corresponding to any given test performance is that chronological age for which the test performance is the average.
2. The mental age corresponding to any given test performance is the average chronological age of people who make that test performance.
These two definitions of mental age do not have the same numerical values. Since they are inconsistent, it is essential, if we insist on using mental ages, that we specify rather definitely which of the two possible kinds of mental age we are using. They are not interchangeable. Both of them may be defended, but the first definition is the one usually followed.
In order to set out in relief the difference between these two definitions of mental age, we may recall the meaning of the two regression lines on a correlation table and their application in this case. When you step on the scales at the drug store, you notice a little table with two columns, heights and weights. You ordinarily read it by saying that your height is so and so. You find this height in the table, and next to that entry you read the average weight of people with your height. You have used the record of a regression
( 269) line. But now suppose that when you have ascertained your weight, you have to find the average height of people who have your weight. Your impulse is to find your weight in the same table and to read the height next to it. But that doesn't work. Another table would have to be used which would be constructed from another regression line. One of these tables shows the average weight of people with given heights. The other table would show the average height of people with given weights. It is the former table in which we are ordinarily interested.
Now, if the same reasoning is applied to a correlation table for test: performance and chronological age, we shall have two regression lines here also. One of these lines, or tables, will show the average test performance for children of given age. The other line, or table, will show the average chronological age for children of given test performance. But these two lines are different and the two tables cannot be used interchangeably. Their practical use would be illustrated as follows. If the age of the child is known and we want to know the average or expected test performance, we use the regression `test performance on age.' If, on the other hand, the test performance is known and we want to guess the child's chronological age, we should use the regression `age on test performance.' When we test children's intelligence, we nearly always have access to their chronological age. We don't need to guess at that. But we need to do a lot of guessing about the child's intelligence. Therefore one of these regressions is of considerable interest and practical importance whereas the other one is of practically no importance. The important regression line in this correlation table is therefore the regression of `test performance on age.' It can be used to ascertain the test performance that is to be expected of the average child of a given or known age.
Figure 1 will assist in making clear this distinction. Let it represent the correlation table for test performance and chronological age. - Let test performance be measured in any terms or units. In the vertical column, x, are represented all the children of age x who took the test, and their test
( 270) performances are indicated by the dots in that column. The average test performance of all these children of age x is indicated at A. If a similar column is erected at each age we should of course find that the older children have higher
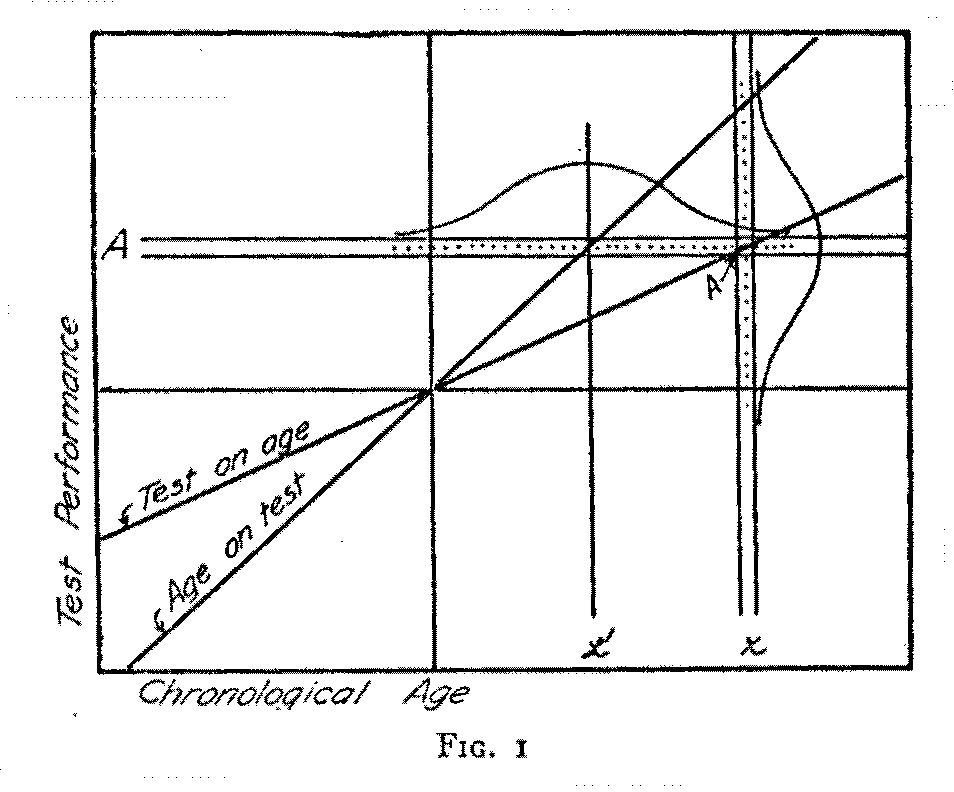
average test performances than the younger children. If the average test performance is located in each column, these average performances will constitute the regression `test on age.' By means of this regression line we can ascertain the average or expected test performance for a child of any given age within the limits of the table. In fact, by the more customary definition of mental age, each of these average test performances is designated as the mental age of the column in which it is found. Therefore, the test score, or performance A is designated as the mental age x because A is the average test performance or score for children of age x. This is the first of our definitions of mental age and it is the customary one.
But in the same table it is also possible to draw another regression line. Suppose that we have collected all the test records with the score A. All of these children will be represented in the correlation table of Fig. I. in the horizontal row at the level X. Each child is represented in such a table by a dot or other suitable mark. Now we may determine the
( 271) average chronological age of all the children who get that particular score A. Let that average age be represented by x' in Fig. 1. We may of course do likewise for every class interval of test performance, and that will give us a set of horizontal rows, each with its own average age. It is to be expected that as we increase in test performance, the average chronological age will also increase. If these average ages of the successive horizontal rows be connected, we shall have the regression line `age on test.'
What is the significance of these two regression lines in our definition of mental age? Let us attempt to define just what we mean by a mental age of eight. If we have tabulated our
data for age and test score in the form of a correlation table like Fig. I, we shall have two alternatives which refer to the two regression lines. Suppose that the x-column represents the eight-year old children and their test scores. We can then determine the average test score for these eight-year old children. We may designate that average test score, A, as the normal performance for eight-year old children and we may argue that this test performance should therefore be called the mental age of eight. When a child attains this test performance, A, we should say that the child has a mental age of eight.
But there is another consideration that makes this interpretation look awkward, although it is the customary one. Suppose that we consider in one group all the children who have this test performance, A. What is their average chronological age? It is certainly not eight unless there is a perfect correlation between chronological age and test performance, which is an impossibility. We therefore find that
the average test performance of eight-year olds is not the same as that test performance, the average age for which is eight. We may, however, select one of these analyses as basic for a definition of mental age. We might say, for example, that a certain test performance is to be regarded as a mental age of eight if the average age of all the people who get that score is eight. That is the second definition of mental age. According to this definition the test per-
( 272) -formance A would be assigned a mental age at x' in Fig. I.
In the practical situation we might proceed along either of these two lines. When a child makes a certain test score, A, we may ask the question, "What is the average chronological age of other children who make this particular test score, A"? In Fig. I this age is designated x'. On the other hand, we may ask about that same child the question, "What is the chronological age, the average test score for which is equal to that of this particular child"? Then, if the child made a test score of A, we should find the answer at x and not at x'. This latter definition is the one commonly implied by the term mental age, but the usage is not consistent and investigators may possibly be unaware of this difference between their mental age norms.
There is another aspect of the logic of the mental age concept which goes contrary to the common sense of the correlation table. In the height-weight example, we found that when the height is known and we wish to ascertain the average weight corresponding to our height, we use the regression `weight on height.' When the weight is known, and we wish to ascertain the average height for our weight, we use the regression `height on weight.' This can be summarized by the rule that we always use the regression `unknown on known.' That is not only common practice but it is also common sense in the use of the correlation table.
But when this reasoning is applied to the correlation table for test score and chronological age, it leads to the less popular definition of mental age. When a child has attained a certain test score, it is the test score that is known and if any estimate; is to be based on the test score, we should be estimating the chronological age by the test score. In other words, we should be using the regression `age on score.' We should then define the mental age of a child as the average chronological age of all children who make the test score of this particular child. According to this definition, a child would be at par mentally if its test performance is such that the average age of all people who make that test score is equal
( 273) to the child's age. That is our second and less popular definition of mental age.
So far we have considered some of the inconsistencies which are the result of using two definitions of mental age. However; either one of these definitions might be adopted and universally used so that we should always know which is which. Some other name might be adopted for the other definition if it were found advisable to use both measures of brightness or test intelligence. My main argument is, how-ever, that both of these definitions of mental age lead to ambiguities when applied to the adult years, and that the mental age concept should therefore be discarded in favor of a more direct and simpler measure of brightness which does not lead to logical somersaults like those of mental age.
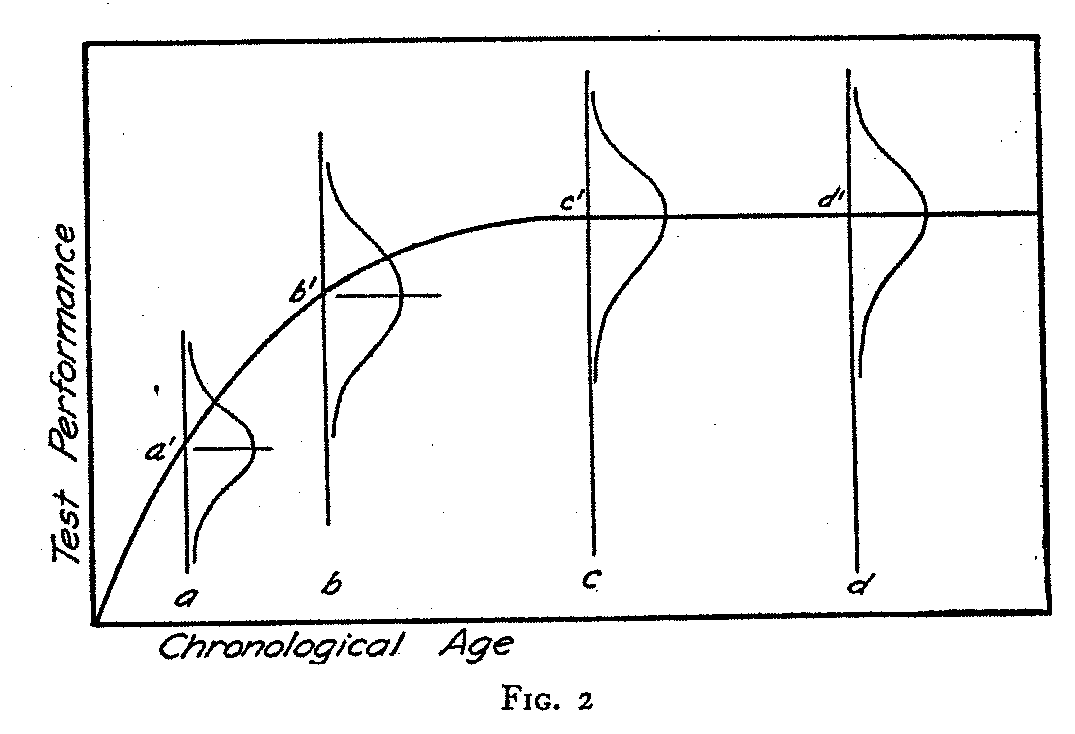
In Fig. 2 I have represented schematically the same correlation table as in Fig. i, except that the age range has been extended into the adult years. It represents an analysis of the first definition of mental age as it appears in the adult ages. At a we have the distribution of test performance for age a. The average test performance at that age is at a' and the distribution of test performance ranges above and below the performance a' as a mean. For our present purpose the question of the normality or symmetry of this distribution does not matter. At a higher age, b, we have
( 274) similarly a distribution of test: performances which range above and below the mean test performance at b'. Naturally we should expect the mean performance b' to be higher than the mean performance at a', because b represents a higher chronological age than a. At the age c which is somewhere in the teens, or perhaps as high as twenty, we have the maximum test performance which our mental age tests can differentiate. The highest mean test performance, c', is attained at the age c. But now the difficulty arises in applying the mental age concept. If we inspect the distribution of test performance at the adult age d, which may be age 40,' for example, we find that its mean test performance d' is no higher than the mean test performance already attained at the age c. If the age c, at which the maximum mean test performance is attained, is found experimentally to be at 16, for example, then it will automatically be impossible to attain a mental age beyond that age. The reason may be in the limitations of our tests which do not measure mental development beyond adolescence, or the reason may be in the possible conclusion that intelligence does not develop beyond that age. At any rate we must deal with the fact that a group of 40-year olds would make a mean test performance which would be no higher than the mean test performance at 16. Now let us look at the first definition of mental age which we are here trying to interpret. It states that the mental age corresponding to any given test performance is that chronological age for which the test performance is the average. It will readily be seen that since the mean test performances c' and d' are equal, we shall have an 'indefinite number of mental ages assigned to this particular test. performance. We have a right to say that the test performance c'. should be given a mental age of 40 because a group of 40-year olds would make a mean test performance of c'. But a group of 16-year olds would also make this mean test performance. Therefore this definition of mental age is entirely ambiguous. A mental age of 40 is the same as a mental age of 16 or of any other age beyond the 16- or 18-year level. The only way out is to revise the definition of mental age.
( 275)
This difficulty is well known to all mental test people. The solution usually given is arbitrarily to call the mean test performance of 16- or 18-year old children the adult level. Walter Lippman in his articles in the New Republic a few years ago, drove home rather effectively the absurdity of insisting that the adult population has an average mental age of 12 or 13 by pointing out that the Army test data constituted as valid an age standardization as the few hundred tests given to school children. We might be able to save the mental age term by revising the definition so that the mental age corresponding to any given test performance is the lowest chronological age for which the test performance is the average. But why use age at all as a scale for mental development when the relation between intelligence and age is imperfect and non-linear? Why not specify test performance on any convenient scale directly related to the test performance itself, instead of twisting it into some sort of age?
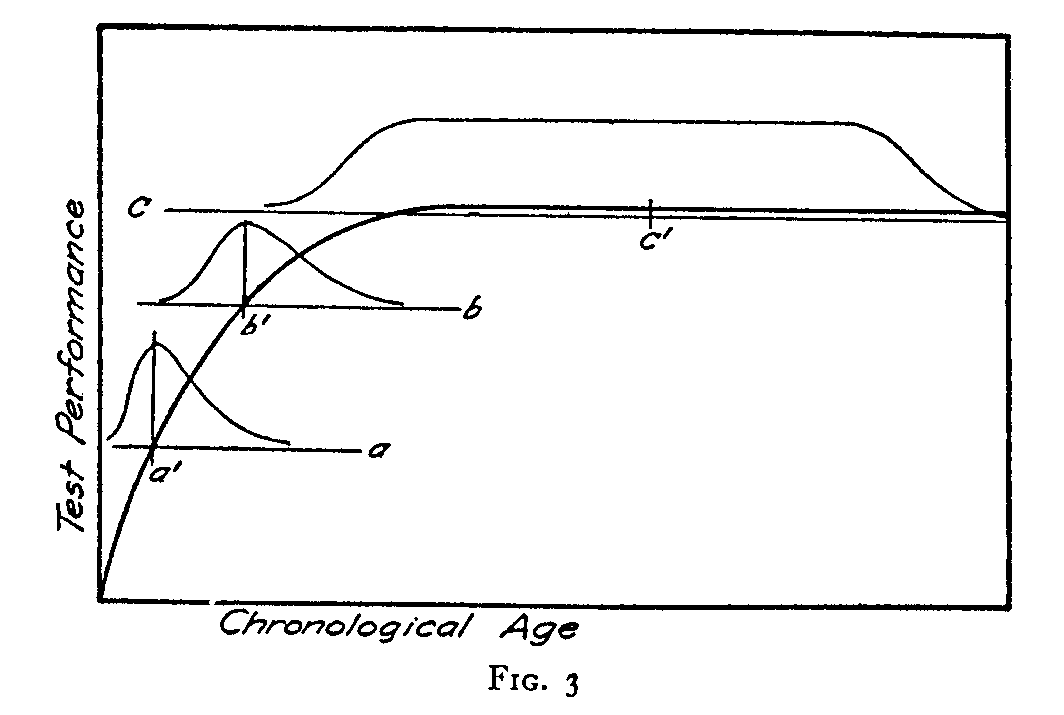
But there remains the second alternative definition of mental age which may be interpreted for the adult years. In Fig. 3 I have represented again the correlation table for test performance and chronological age. In this figure the horizontal section a represents all the people who have the test performance a. They vary in age, of course, and the distribution of age is represented diagrammatically by the
( 276) frequency distribution with its mean a'. In the same manner the horizontal section b represents all the subjects whose test performance is b and their ages are diagrammatically represented by the frequency distribution with its mean at b'. But what about the distribution of ages for the test performance c? Since this is the mean of the adult test performance the age distribution stretches over the whole range of life. The mean age c' would be perhaps 35 or higher. Even if we should decide to determine this mean age, we should find it impossible to do so without ambiguity because the mean age for this distribution, and for those immediately below it, is largely determined by the number of individuals that we should select at each age. Should we select the same number of people at each age in this distribution? Or should we select such a frequency of individuals at each age that the distribution of age corresponds to the frequency of each age in the general population? Such a distribution might be determined from the mortality tables. Since the mental age scale is intended as a scale of mental development, there is no sense in translating test performance into age with all these entirely unnecessary troubles. In the case of the first alternative definition of mental age, we found that the term could be saved from absurdity, if we must have it, by redefining it. But in the nature of the case, there is probably no way in which the second alternative meaning of the term may be redefined so as to avoid ambiguity.
All of these difficulties would be avoided entirely if we should discard the awkward mental age concept and proceed instead as follows. When a child has been given a mental examination of the Binet type, or any other, we might ascertain the child's chronological age. Then we might consult our norms and say that this child's mental development, compared with other children of the same age, has a percentile standing of, say, 70. This would be extremely simple. It would mean that this child is a little above the average in intelligence among children of its own age. It would mean that 30 per cent of the children of the same age are brighter, and that 70 per cent are less bright. The
( 277) intelligence quotient would be discarded along with the mental age concept on which it depends and the percentile standing of the child would be used instead. Such questions as the constancy of the intelligence quotient would still be with us but we should use the percentile standing of the child among others of its own age as the index, instead of the intelligence quotient. We should be inquiring whether a child keeps his relative standing among other children of the same age as he grows older.
For many statistical studies it might be preferable to use the sigma standing of the child instead of the percentile standing. The test performance of any particular child might then be designated either by his percentile standing or by his sigma standing, in every case compared with other children of the same age. If such a system were in use, we should have no difficulty whatever at the adult level. We should measure mentality there also by stating the person's percentile standing, or his sigma standing, compared with other adults or with others of the same age. Our measurement system would have continuity and sense, a satisfaction that cannot be attained with mental ages and intelligence quotients.
If we should measure mental development in terms of relative standing, either in terms of percentile ranks or the standard deviation, it would still be possible to say that this particular child of eight is as bright as the average ten-year old child. That is the comparison that the mental age terminology is intended to facilitate, but there is nothing to prevent our making such statements wherever wanted without using mental ages. In practical situations, both types of comparison may be made, one directly with other children of the same age and one comparison with children of any other given age. Then a given eight-year old child's mentality would be described by a percentile of, say, 70 for his own age, and he could also be compared with ten-year old children by saying that he would have a percentile of, say, 50 among them and so on. The child could be compared with children of other ages by the same set of tables or norms.
( 278)
Binet may still be given credit for having introduced certain types of objectivity in mental measurement but his invention of the mental age concept was an awkward and unfortunate one. It is of course possible to retain the terminology of mental ages and intelligence quotients and to limit these terms to tests for children. But since these terms become nonsense when applied to adults, there would always be the question as to what age shall be the practical limit for their use. Would it not be better to discard mental ages and intelligence quotients and to adopt a measuring system, already universally known, which is extremely simple and which has the advantage of continuity so that it may be used for all ages?