The Verification of Social Measurements Involving Subjective Classifications
Stuart A. Rice and W. Wallace Weaver
THERE can be no doubt of the prestige possessed by quantitative methods in the minds of social scientists of the present generation. We are not concerned in the present paper with examining the causes of this prestige, with the advocacy or discouragement of measurement as a type of method, or with discussing its general limitations or possibilities in social science. Our purpose is to point out the inevitable subjectivism of a certain type of so-called measurement, and to present a partially developed technique for determining the extent of variations among separate investigators who attempt to measure the same material. This technique relates, that is, to the problem of verification, and permits the calculation of a coefficient which will throw some light on the validity of the measurements.
As illustrative of the field of inquiry to which our argument relates, we have conducted an experiment in the measurement of newspaper content, employing the methods developed by Professor Malcolm. M. Willey in his noteworthy study of the country press in Connecticut.[1]
( 16)
Of numerous attempts to measure the content of newspapers, Willey's is the most thoroughgoing, and the most adequate in the perfection of technical method.
He has made every effort to achieve objectivity and he has covered an extensive range of newspaper material.[2] His work, in fact, represents the culmination of a series of experiments in newspaper measurement conducted for a number of years by students of Professor A. A. Tenney at Columbia University. Professor Willey had the advantage of building upon these earlier efforts, and he brought to his immediate task an intimate understanding of Connecticut journalists acquired by actual experience on a newspaper staff in that state.
The importance of the attempt to classify news has been widely recognized [3] and requires little attention here. It rests upon the assumption that newspaper content is a reflection of the interests and attitudes of readers, or a stimulus thereof, or both. That is to say, measurements of news, if they can be scientifically made, are in effect measurements of one important type of "social force." [4]
Nor is it difficult to see the importance of measurements of other similar materials in which the same types of problems are encountered. Some analogous attempts with which we chance to be familiar may be mentioned: Mr. H. G. Loonier, one of our colleagues, has attempted to determine trends of interest among social workers over a period of several decades by classifying according to subjects the papers presented at successive annual
( 17) meetings of the National Conference of Social Work.[5] Mr. Howard Becker, another colleague, has arrived at some indications of trends of interest among American sociologists by classifying articles published in the American Journal of Sociology.[6] For this purpose he employed the classification established some years ago by that publication for the arrangement of its abstracts of current literature. The development and use of this classification is itself a further illustration of the type of inquiry being cited. Professor Donald R. Young, also a colleague, has given considerable attention to the possibility of measurements of content of moving picture films.[7]
Still further afield from newspaper measurement, but nevertheless involving the same essential difficulties, are studies which require the classification of individuals according to social type, in which completely objective criteria are unavailable. An important illustration of this kind is the paper on parole violation by Professor Ernest Burgess, appearing elsewhere in SOCIAL FORCES, and there discussed by one of the present writers.[8]
In all of these inquiries, and others which they represent as types, the central purpose has been to replace subjective appraisals by objective measurement. For example, instead of estimating (subjectively) that a given newspaper "devotes half of its space to sensational news" Professor Willey seeks to give us a depend-
( 18) -able percentage resulting from the application of a ruler. The actual scientific accomplishment of these various efforts, then, depends essentially upon the degree to which they are free from those same personal and subjective influences upon judgment which they were developed to remove. It is a cardinal principle of scientific method that its results should be verifiable. That is, the same results should be procurable by two or more competent investigators working independently under the same conditions; allowing, of course, for a margin of error. Two land surveyors should arrive, within reasonably narrow limits, at the same statement concerning the area of a field. Two diagnosticians should be able to start a patient toward the same general division of the hospital. Would another investigator be likely to give a parole violator the same personality classification as does Professor Burgess? Does Professor Willey's technique lead to a close correspondence between the measurements of the same newspapers obtained by different investigators? These questions are empirical. The answers are to be obtained by trying them out.
We will first describe the parts of Professor Willey's technique which pertain to our problem; second, we will examine some of the theoretical assumptions which underlie his procedure; next, we will present a technique of our own for measuring the amount of concurrence obtained by independent investigators in using his classification; lastly, we will present some results of using this technique by members of graduate classes at the University of Pennsylvania.
Professor Willey's method is simple in its main outlines. He classifies all printed matter exclusive of advertisements in the papers analyzed, placing each news item in a single category. The classification is based upon "the what" contained in each item. He says:
"In the newspaper offices there is recognized in each story a feature known as the what.' This is the fact of chief concern; it is the detail or cluster of details that makes the editors believe the particular news story will be of interest to readers. It is the fact that is stressed in the opening paragraph of the account; hence it is oftentimes called the lead.' It is the fact or phase usually featured in the headlines. It is an invariable rule in newspaper writing that 'the what' should be placed in the first line or two of the first paragraph. If the news story is telling of a murder, murder ('the what') is stressed at the head of the column; if the fact is robbery, robbery must be introduced at the outset. The modern editor pushes his news tidbits to the fore. This is of tremendous importance and value in analyzing newspaper content, because it gives the basis upon which any item or news story can be assigned to its proper category. The procedure in classifying newspaper content is to ascertain 'the what' in each item, and upon the basis of this make the assignment of the item to the classification category,"[9]
The system of categories that he has developed contains ten major headings and 49 minor or sub-categories into which the content of any newspaper may presumedly be fitted.[10] This classification includes, it may be noted, a major category of "miscellaneous" and a sub-category of "unclassifiable." The latter includes "items” ‘the what' of which cannot be determined, and the content of which does not make it possible to place definitely in any of the other categories.[11] In his Connecticut study, Willey ascertained the variations in the relative amount of space given to particular types of subject matter by different newspapers, and by the
( 19) same newspapers over different months of the year. This involved the establishment of norms among the papers included in his inquiry.[12]
Some of the theoretical difficulties underlying this procedure will now be examined: Unless we accept the position of the extreme behaviorists the essential entities in which social scientists are interested are subjective in character. Thus psychologists are interested in "intelligence" and social psychologists in "attitudes." Neither of these concepts are susceptible of direct measurement by any known means. Their existence is inferred from behavior to which, presumedly, they give rise. Obversely, in measuring behavior the psychologist is ascertaining something concerning hypothetical subjective realities back of the behavior. He infers that these subjective entities are variable as between individuals because their behavior is variable, and he may even posit a mathematical curve expressing their presumed mode of variation.
The behavior measured in these cases, whether verbal or otherwise, is objective. By this is meant that it impinges upon and stimulates the investigator's sense receptors. The data appear to have their sources in objects (ocher persons) of the investigator's "outside world," and they reach him by means of such material agencies as light and sound waves. Moreover, the measuring process is objective. That is, the meaning given to the data for the purpose in hand, by a previously agreed-upon system of relationships between sensations and their interpretation, is definite and precise. No room for personal judgment on the part of the mental tester need be left in the testing process, so long as all persons concerned understand and concur in this system of relationships. If the relationships between sensations and their subjective interpretation are not precise, on the other hand, the measuring process is no longer regarded as objective and becomes subjective. It is doubtful whether it should any longer be called a "measuring process."[13]
Now the news content of a newspaper, as data, is also objective. It reaches the individual's sense receptors by means of light waves. Moreover, the purpose in hand, and the relationships between the data and the interpretations placed upon them in reference to this purpose, may be such as to permit an objective measuring process. For example, Professor Niceforo has classified the epigrams of Martial according to their length and the odes of
( 20) Horace according to various criteria with, respect to the strophes of each,[14] developing a number of frequency distributions in each instance. These measurements are objective. Similarly, if it should be agreed that all news appearing on a newspaper page headed at the top by the word "Financial" is to be classified as "financial news," the measuring process is reduced to calibration, and is objective. But there is usually no agreed-upon relationship between newspaper items and the interpretations required for classification in one of Willey's categories. The meaning of a news item, for the purpose in hand, is not precise. It becomes a matter of opinion or judgment whether it should go in one category or another. When this is the case, the "measuring process" must be regarded as subjective.
For example, a certain newspaper story may refer to a lease by the American government of certain oil fields to a commercial interest. Whether I shall place this item under Willey's category one, "political news, domestic" or under his category eight, "industry, commerce, finance and transportation" seems to depend upon the significance which the item has for me individually. If I have previously been interested in the oil scandals at Washington and see in the present item a continuance of Republican policy which will give campaign material to the Democrats, the item will impress me as belonging in category one. If on the other hand my attention is centered on the effect which the new development will have upon the present competitive situation in the oil industry, and in the price of securities in the stock exchange, I will think of the news as primarily economic and place it in category eight. The difficulties which this illustration presents are not dependent upon the particular items in Professor Willey's system of categories, but would appear in any similar system, however minutely it might be sub-divided, unless one were to resort to the unlimited number of classes involved in some system of combinations.
The distinction with which we are dealing is analogous to that between a "true-false" and an "essay" type examination. In the former the proposition which the student makes (i.e., "this is true" or "this is false") is limited to a form where it may be arbitrarily adjudged correct or incorrect. In the latter, the student's propositions fall within no prescribed forms, and must be graded by the instructor by some process of individual, that is subjective, appraisal.
The unreliability which attaches to the results of classification because of its subjectivism is in certain respects reduced, though not eliminated, when all of the work has been done by a single skilled investigator. This is clearly indicated by Willey's own study. We can assume that he employed the same subjective standards in measuring paper A. as in measuring paper B. Comparisons between these papers therefore have validity, because we assume that the investigator's bias is a constant. The difficulty would arise should we attempt to compare a classification of paper A by one investigator with a classification of paper B by another. Or, to take a case which might arise, suppose another investigator should make a study similar to Willey's of the country press in Pennsylvania, and should attempt to compare the proportionate space devoted to certain types of news in this state with those which Willey found in Connecticut. The variations between
( 21) the two sets of measurements might not be due to actual differences in the newspaper content, but rather to the differing subjective standards of the two investigators with respect to the process of classification.
It will be evident, if this type of inquiry is to develop, that some means are required for determining the amount of variation between or among the results obtained by different investigators in classifying the same material. It may be assumed that investigators of American newspapers will have the same general cultural back-ground with respect to social values and the same general familiarity with public affairs.[15] If empirical tests indicate that such investigators can so familiarize themselves with a given technique as to arrive at measurements which, within a narrow range of error, may be treated comparatively, then cooperative labor becomes a possibility in situations where, on theoretical grounds, it seems unsafe to compare the results attained by more than a single investigator working independently.
The technical problem confronting us then is two-fold: First, may the variability among the class distributions of the same news items by different investigators be measured? Second, will the variation, if ascertained, be sufficiently low as to indicate the existence of comparability in their results, if applied to different material? In our endeavor to answer these questions the members of two graduate classes at the University of Pennsylvania were asked to classify a series of newspapers in accordance with Willey's 49 categories.
The measures of variability in general use among statisticians did not, of them-selves, seem adequate for our purpose. The average deviation (symbolized by A.D.) and the standard deviation (symbolized by e) arc both measures of dispersion from a single norm.[16] Since the norm, or aver-age, may itself be great or small, the size of deviations from this norm have comparative significance with reference to the size of the latter.[17] Pearson, therefore, developed a coefficient of variation (symbolized by V) which expresses relative variability by relating any of the measures of absolute variability (such as A.D. or σ) to its respective average.[18] But again,
( 22) this coefficient refers to dispersion from a single norm, whereas we were seeking a single composite coefficient of variation with respect to 49 mutually exclusive categories which together exhaust a constant total.[19]
It was in the latter fact that the difficulty of expressing the aggregate variation was found. Each single investigator was dealing in the case of each newspaper with a fixed number of inches of material. If a news item were classed by an investigator in one category, it was not classed in another. If it were taken from one category, thereby affecting the mean and the measure of deviation in that category, it was at the same time placed in another category, thereby likewise changing the mean and the measure of deviation in the second category as well. Not one of the 49 categories, in other words, could be assumed to vary in volume (as among individual investigators) independently of the variations among all of the other 48 categories.
A composite measure of variation should be directly responsive to changes in classification which decrease or increase the aggregate agreement among the investigators. That is, if one investigator re-classifies an item in such a manner as to decrease the total amount of agreement among a group of investigators, the coefficient of aggregate variation should increase proportionately. Conversely, if his reclassification should increase the total amount of agreement, the coefficient should decline proportionately. Coefficients of variation for each of the 49 separate categories are useful in comparing the ability of the investigators to reach agreement as between individual categories. But they do not aid us, for example, in discovering whether the investigators as a group are in closer agreement in measuring today's paper than they were in measuring yesterday's. The conditions for a composite measure of variation are not fulfilled by a simple average of the 49 individual coefficients of variation, be-cause the amount of material in the separate categories varies greatly, and re-classification of an item in one class would have greater proportionate influence in the composite coefficient than would reclassification of the same item in another class, the proportionate distribution in each by the several investigators being the same. If the coefficient of variation in each category be weighted by the mean of the category, however, and if the sum of these weighted coefficients be related to the sum of the means of the categories, we seem to have a measure which fulfills the required conditions. We will call this a coefficient of aggregate variation and give it the symbol VA. Since the coefficients of variation of the individual categories are functions of their respective means, the calculation of VA can be made directly by summing the average deviations and the means of the categories. Thus
VA = (Σ (M x (100 A.D.)/M) / ΣM = (100(ΣA.D.)) / ΣM
That is, the coefficient of aggregate variation is equal to one hundred times the sum of the average deviations of the separate categories divided by the sum of the means of the separate categories. Since the sum of the means will be a constant no matter what the distribution within the several categories may be, VA will fluctuate up and down responsive to any increased or decreased
( 23) variability in any one of the categories, and do so proportionately to the mean of the category. The transfer of an individual news item from one category to another may lower the coefficient of variation (V) of both categories, may raise it in both categories, or may lower it in one and raise it in the other. In any of these situations, the coefficient of aggregate variation (VA) will reflect the importance of the reclassification with respect to the total amount of agreement among the investigators.
We feel that the first of our two technical problems, therefore, may be answered in the affirmative: the variability among the class distributions of the same news items by different investigators can be measured. We present next the experimental results already referred to.
The students of two graduate seminars in sociology at the University of Pennsylvania, both under the direction of Professor Rice, were set the task of measuring each of a series of five newspapers in accordance with Professor Willey's system of categories. The students numbered twenty-two. Of these, nine were instructors or assistants on the staff of the University. Several others were teachers and social workers in responsible positions. Of the five newspapers, three were daily editions of Philadelphia evening papers, one a daily edition of an evening paper in the smaller adjacent city of Camden, New jersey, and one an edition of a suburban paper serving two residential communities outside of Philadelphia, but within the metropolitan area. Each student was provided with a detailed description of the Willey categories, reproduced from the appendix of his Connecticut study, and the newspapers were distributed at weekly intervals. A discussion of the problems which arose was held at the end of each week.[20]
In addition, Professor Willey kindly coöperated in the experiment by measuring papers numbers one, three and four, in order to afford a basis for comparison. No quantitative computations of deviations from his measurements by the group were made, but his marked copies served as a guide in answering certain questions which arose with reference to the technique.
The five papers distributed, the number of students measuring each, the mean of the total news space measured in column-inches, the average deviations from the mean and the coefficients of variation are shown in Table I.
In spite of the general high competence of the investigators participating, various gross errors were indicated on the reports submitted. The total number of inches of space reported gave a first check, and doubtful reports were checked over with the individuals concerned. That is, striking deviations from the mean total of column-inches seemed to indicate either an omission of certain material, the duplication of measurements, the inclusion of extraneous materials, or marked carelessness in some other direction. In one case where deviations were large it was
( 24) found that a student had omitted one section of a paper. In another instance, measurements which were excessively high revealed that the student had used a ruler containing both centimeters and inches, confusing the two at times. Another student included advertising material in. his first measurements. All such results were discarded in all calculations. It may be pointed out that in general the grand totals of each investigator agreed better on the last three papers than on the first two.
In tabulating the reports of the individual students, we found it necessary to recognize the fact that the members of the group were not constant from paper to paper. While calculations which included reports from the entire number of readers did provide a basis for comparing variability among news categories in any single newspaper, they did not give comparability with respect to the coefficients of aggregate variation as between newspapers. We therefore divided the readers into three groups. Group A contains the variable number of "all persons" submitting measurements in the case of each paper. Group B contains thirteen
persons who measured papers numbers two, three, four and five, and Group C includes five students who measured all papers. It was assumed that the coefficients of aggregate variation for Groups B and C would disclose any tendency toward improvement (decreased variation) in the course of the experiment. Coefficients of variation from the mean within each category (100 A.D. / M) were calculated for
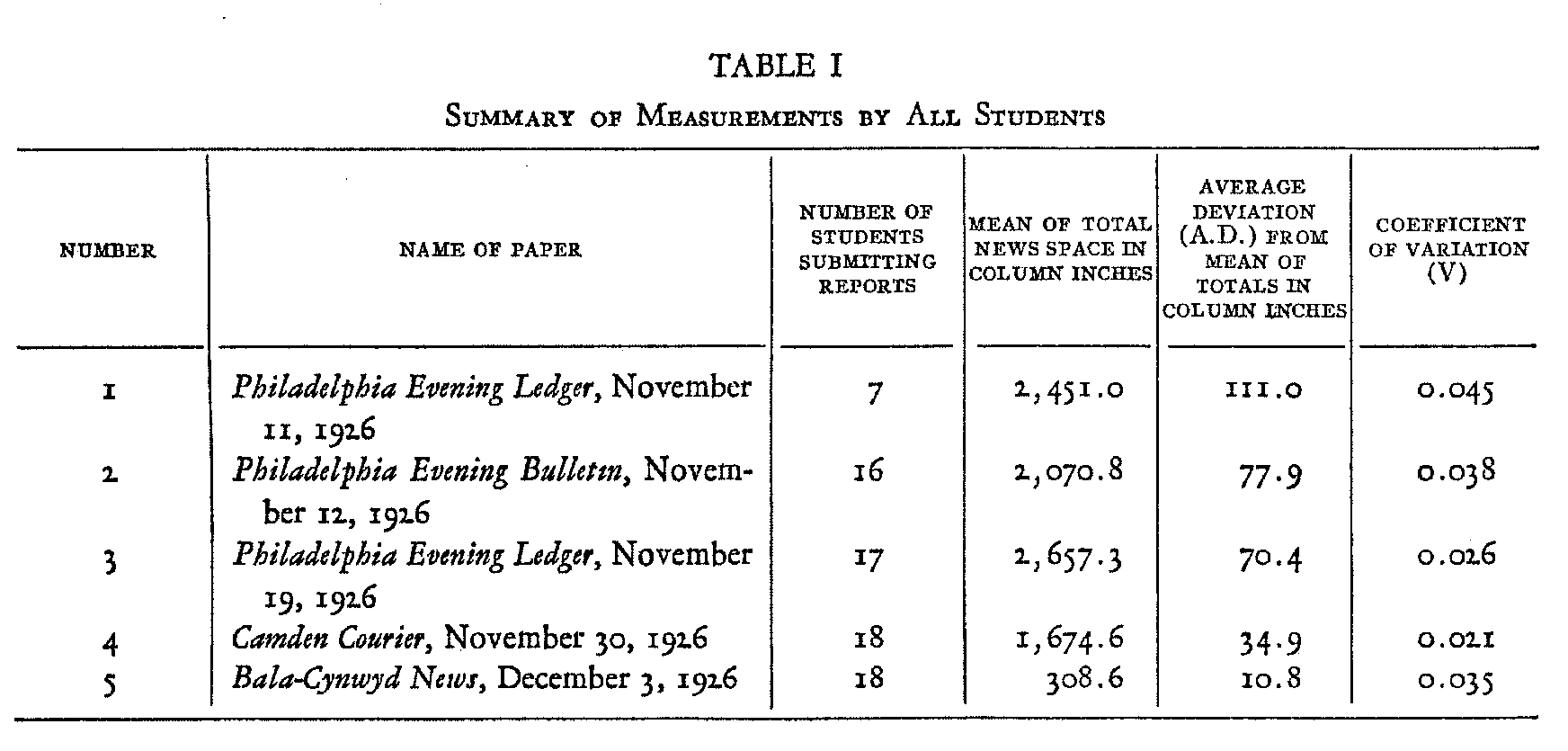
Group A for each paper, but were not calculated for Groups B and C. Table II presents for group A, and for each of a. selected number of categories with large deviations, the Mean in inches (M) the Average Deviation in inches (A.D.) and the Coefficient of Variation (V). Table III presents the corresponding data for a selected number of categories with low deviations.
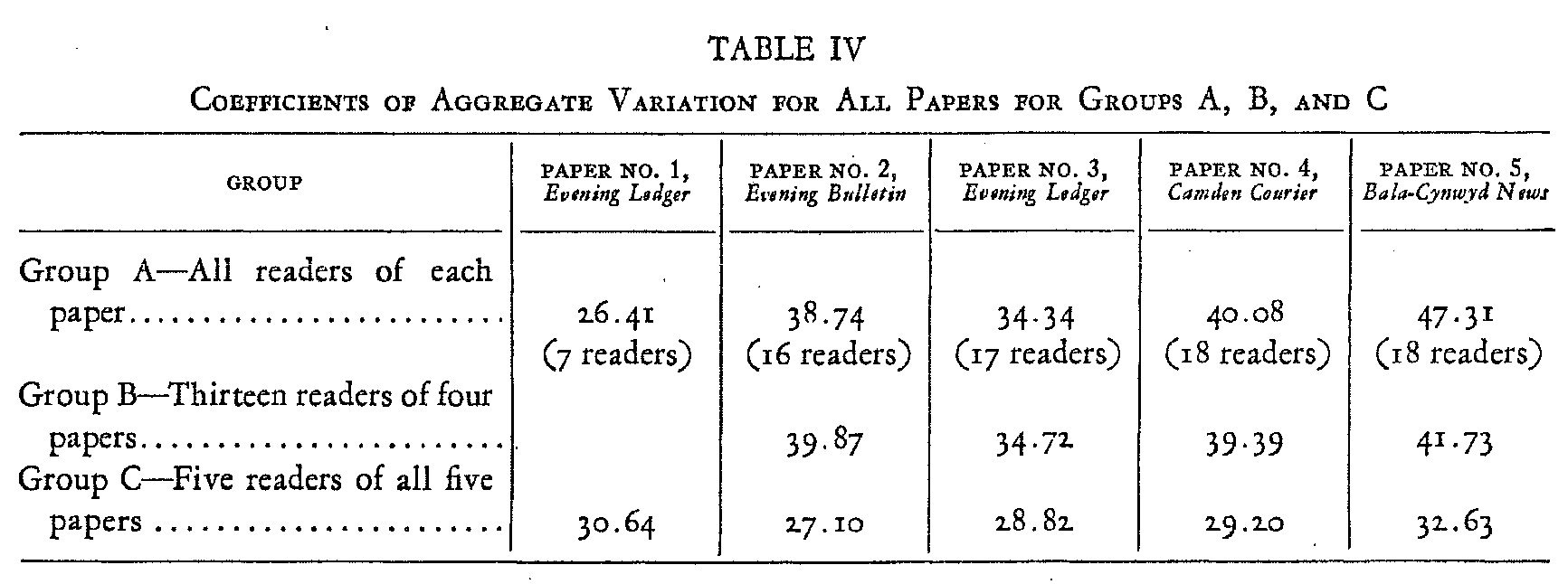
A coefficient of aggregate variation was calculated for each paper in every group, according to the method previously de-scribed above. These are shown in Table IV.
An examination of data summarized in Tables II and III indicates that the most marked relative variability is found in the
( 25)
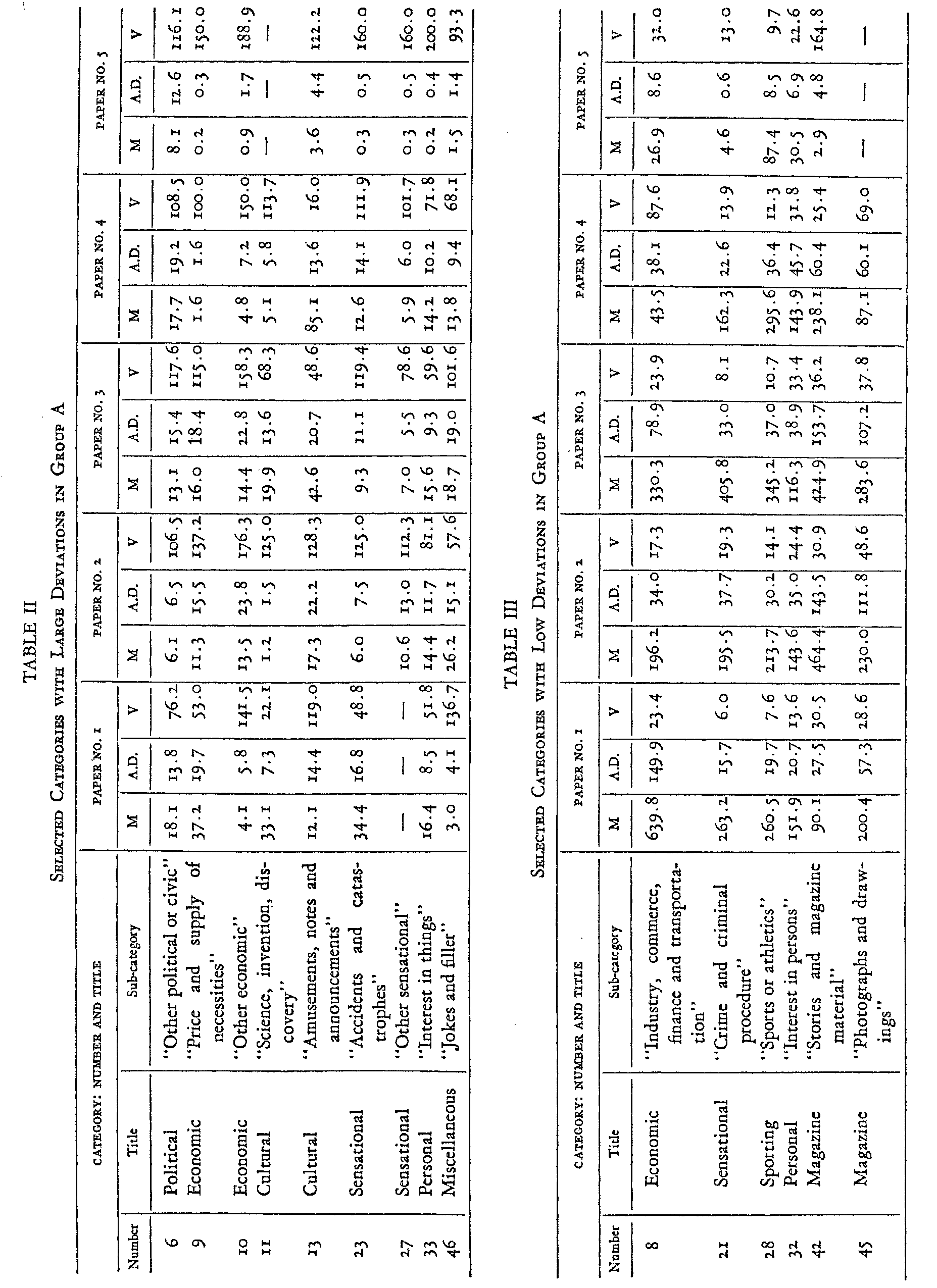
( 26) categories with the smallest means while the smallest relative deviations are to be found in those categories with the largest means. It is probable that the lower variability in the categories with large means is due, in part, to the composite character of their content, which permits many of the variations which might be noted in a detailed statement to cancel out in combinations. Such an explanation certainly applies to category Eight into which most students have thrown almost the entire section on financial news and category Twenty-eight, in which the entire sporting section has been placed as a unit. There is seldom any evidence to indicate a detailed analysis of the sports pages.
The high rates of deviation in the categories with low means may be explained in part by the fact that frequently no entries are made by one or more students for a given category, while others assign certain articles to those categories on the basis of different subjective attitudes. Strict comparability between the coefficients of variation in categories with large and small means, in fact, could only be secured if the number of separate items were in each case the same. That is, the average size of the individual news items would have to bear the same ratio to the
size of the mean in the case of large and small categories.
It was anticipated that there would be a progressive diminution in variability within the several groups with each succeeding paper. It was assumed that the discussion each week of the difficulties encountered would tend to bring about greater uniformity. The evidence on this matter contained in Table IV, however, is not wholly satisfactory. Groups A and C show a marked improvement between the first and second papers, but thereafter an opposite tendency, so that the greatest deviation appears in the final paper. This may be due in part to the smaller size of the latter, as it has been seen that small categories are accompanied by proportionately large relative deviations. Group B likewise reveals an improvement between the first and second paper for this group, with a subsequent progressive in-crease in variability. It may be that this result, contrary to the expectation, results from an increase in carelessness on the part of the readers, incident to the laborious and uninteresting nature of the task, once its novelty had passed. On this point consult footnote 20 above.
With these illustrative results before us, we next take up the second technical problem referred to above. Do the coeffi-
( 27) -cients of aggregate variation have significance as indicators of the presence or absence of comparability in the work of separate analysts of different newspapers? First of all, at this point, we wish to reiterate that the question is essentially empirical. But our own findings are exceedingly meagre and the conditions under which we obtained them were inadequately controlled. We do not wish to draw conclusions from them. Nor have we been able to solve some of the theoretical questions involved.
Many indices of variable functions are useful for comparative purposes without providing a measure of comparison with the limits of possible variation. For ex-ample, the Bureau of Labor Statistics reports fluctuations in employment, but cannot state the absolute number of unemployed. Psychologists have been perplexed by uncertainty concerning the "zero" of intelligence at one end of their scale of mental measurement, and its upper limit at the other. Our own perplexity is not altogether dissimilar. Our coefficients of aggregate variation seem useful comparatively, but they do not provide an uncertain answer to the question raised in the preceding paragraph, which seems co require knowledge, first, of the possible limits of variation of VA, and, second, of the VA which would be most probable on a chance distribution of news items among categories.
The possible lower limit of VA is of course 0.0. The latter would represent the aggregate variation if all of the investigators placed exactly the same percentages of news space in each of the categories.[21] There would then be no deviations from the mean in the several categories, and the numerator in the equation for VA would be 0.0.
The possible upper limit of this coefficient, however, varies with the number of investigators and, under certain conditions, with the number of categories. It appears to approach, but never under any circumstances to reach, an asymptote of 200.0.
The maximum possible amount of variation (or disagreement) is reached in any given case if each investigator classifies 100.0 per cent of the news in a category in which all other investigators classify 0.0 cent. This condition may only be obtained when the number of categories is at least as numerous as the number of investigators. When this condition is met, and letting the number of investigators be symbolized by G, it has been observed that
Upper limit VA = 100 (1 + ((G-2)/G). Thus,
If G = 2, the upper limit of VA = 100.0
If G = 3, the upper limit of VA = 133.3
If G- = 4, the upper limit of VA = 150.0
If G = 5, the upper limit of VA = 160.0
If G = 6, the upper limit of VA = 166.6
If G = 10, the upper limit of VA = 180.0
If G = 100, the upper limit of VA = 198.0
If G = 1000, the upper limit of VA = 199.8, etc.
This raises the question whether, in our own findings for example, the coefficients of aggregate variation procured from a group of four investigators are comparable with those procured from a group of five. It is our opinion, since the upper limit of the possible range is wholly theoretical and not actually approached, and since, further, the difference in personnel of the two groups introduces variables of un-defined character, that no greater error is
( 28) introduced when such a comparison is made.
If the number of categories were to be less than the number of investigators, the possible upper limit of the coefficient of aggregate variation would be reduced, as compared with its limit if the number of investigators remained the same, and the number of categories were equal or greater. The upper limit might then be considered as a function of two variables, the absolute number of investigators and the absolute number of categories.[22] The equation which would represent the variable upper limit in this circumstance has not been developed.
Even greater perplexity attached to the rôle of chance in the distribution of news items by investigators among categories. Since a coefficient of 0.0 indicates complete "success," and since the upper limit of the coefficient would indicate a maxi-mum degree of "failure," fully as improbable as maximum success, the scale of relative success should seemingly start from a VA which would represent the most probable chance distribution of items and hence have a relative position of 0.0 (in the scale of "success"). The analogous theory of a "true-false" examination may again be cited for illustration: If a grade be given for all correct answers and no deduction be made for wrong answers, then the average student who "guesses" would be right half of the time, and start with an initial probable grade of 50 per cent, even though he knew nothing of the matters involved.[23] It is obviously fairer to arrange the grading system in such a way that a grade of 50.0, representing the chance distribution of answers, (on the basis of marking named) will be counted as 0.0. The other end of the scale would of course be 100.0.
But in the case of newspaper measurement, the most probable distribution of items for each investigator would seem to be, in theory, one in which equal proportions of the total were placed in each category. Such a distribution, for all investigators, would result in a coefficient of aggregate variation of 0.0, which by definition we regard as maximum "success." In other words, the most probable distribution seems to be one in which all investigators agree, and the scale of "success" for which we were seeking seems to vary between 0.0 and 0.0! It is obvious that the degree of "success" (relative agreement in classification by investigators) cannot be deduced from the coefficient of aggregate variation by this line of reasoning, unless some more realistic interpretation be given to the concept of "chance distribution" for the present purpose. This we have been unable to do.
What we feel ourselves to have accomplished in this article, therefore, is
to raise an important problem concerning a promising and growing field of
research, and to suggest a partial means of dealing with it. We should welcome
criticisms of our argument and further suggestions, especially from
mathematically-minded readers.