The Fundamental Laws of Human Behavior
FOURTEENTH LECTURE
Max Meyer
Table of Contents | Next | Previous
Spatial perception. Inherited responses to spatial form. Acquisition of unitary groups of conductors serving all objects of the same design. Mutual attraction of nervous processes of equal strength. Melody and harmony. Two kinds of tonal similarity. Neurons applying their specific resistances in various degrees to a variety of processes. Rhythm equals subjective grouping of objectively uniform excitations. Habits of performing group motions consisting of one chief and one or several preparatory movements. No counting in rhythmical perception. Why all common rhythms are of the doublet and triplet kind.
THE function of the nervous system is said, by some, to have three aspects. But to distinguish them one must narrow his view to an exclusive consideration of the sensory function, the motor function, or the collecting and redistributing function of the system, of which none can have any separate existence. How artificial the separation of these functions is, appears from our previous discussions. The function of the nervous system is always one which carries sensory excitations to motor points over short or long, relatively simple or complex paths. A distinction of different aspects of this single function merely offers convenient headings under which to place chapters of a prolonged discussion. Thus we may say that we are now to consider a certain sensory aspect of nervous function, namely that
(182) which is customarily referred to by psychologists under the name of the perception of space. The sensory points here in question are mainly those of the cutaneous surface of the body and the retinas of the eyes. The problem which concerns us is, broadly stated, this: How can we explain the fact that group stimulations of a particular geometrical design, occurring now here, now there on the sensitive surface, are capable, within limits, of calling forth identical motor responses although the sensory elements stimulated may be either entirely different or only partly identical?
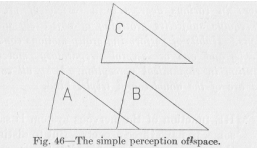
To state the problem less abstractedly, let us take an example. A triangle is before our eyes. We move, and the triangle appears on a different part of the field of vision, at B instead of at A, in Figure 46. The sensory elements stimulated in both cases are partly different, partly identical, as the figure shows immediately. We move again and the triangle appears again on a different part of the field of vision, at C. This time altogether different sensory elements are stimulated. In all three cases our reaction is about the same; if it is a speech reaction it consists probably in our pronouncing the word triangle. Whatever the reaction may be, on general
(183) principles of theoretical explanation we must be able to conceive of it, because of its definiteness and identity, as the result of a nervous flux proceeding somewhere within the nervous system from a definite single point. Our problem, then, consists in showing the possibility of all the nervous processes which come either from A, or from B, or from C, uniting in the same single point within the nervous system. From this point on toward the motor periphery the nervous process may then undergo all the influences hitherto described in general, leading to all kinds of variations and combinations of motor effects.
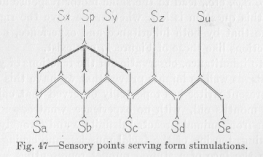
Figure 47 contains two classes of points which are marked with letters. The points marked Sx, Sy, Sz, Su, Sp, are those among which the central point just mentioned is to be found. They are quasi-sensory points, not located in the sensory periphery of the nervous system, yet to be regarded, in the light of all our previous discussions of function, as if they were truly sensory points. In them are collected the conductors which unite the genuine sensory points Sa, Sb, Sc, Sd, Se into the groups spoken of above as essential for the so-called perception of space. In the point Sx of the figure two true sensory points are grouped together, Sa and Sb. One of these, Sb, is also
(184) grouped with Sc, in the quasi-sensory point Sy. All three, Sa, Sb, Sc, are united in the quasi-sensory point Sp. From each of the points Sx, Sy, Sp a definite chain of neurons, not given in the figure, leads to a definite motor outlet. Suppose, now, that three other sensory points are united in another quasi-sensory point Sp’, (not shown in the figure), three others in Sp’‘, etc., and that from all these quasisensory points Sp, Sp’, Sp’‘, etc., the excitation is carried to the same motor point Mp. Thus group stimulation of a particular geometrical design, though occurring now here, now there on the sensitive surface, can by way of Sp, Sp’, Sp’‘, etc., lead to the same motor response at Mp. Only this question is left, whether we have the right to assume that by both inheritance and experience, neuron connections like those of Figure 47 can exist.
As to inheritance, observation of the reactions of young animals as well as infants proves that we have this right. The present writer has repeatedly observed that children a few months old, with no experience whatsoever as to danger from animals, reacted definitely and strongly with shrinking, tension of the facial muscles, and crying when shown the face of a stuffed puppet representing a little
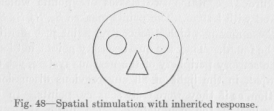
pig of simple features like those of Figure 48. Since the reaction was the same in the case of different children and of somewhat different puppets, the conclusion is to be drawn that it was a reaction to the common features of
( 185) these puppets, consisting in a circular head, two conspicuous circles within, the eyes, and a conspicuous triangle, the snout, as shown in the figure. Obviously, then, the sensory points of the child's eyes are by inheritance combined into a large number, perhaps thousands, of groups so that all the points stimulated by an appearance, in upright position, more or less like that of Figure 48, send their excitations to a single motor point or a single central point whence the flux is redistributed to cause the definite reactions mentioned. There are probably also many other kinds of such groups, of other shapes, inherited by each individual of the human and animal race. In animals, too, similar definite reactions to the appearance of an object never experienced before have been reported by various observers.
The other question is whether a grouping of sensory points like that of the diagram of Figure 47 and the further grouping (above mentioned) of such points as Sp, Sp’, Sp’‘, mentioned above as serving the same geometrical design on the sensitive surface, can be acquired during life. For this it is merely necessary that when a definite group of the sensory points on the retina or skin is stimulated by an object, a definite motor response is strongly called forth by a certain additional property of the same object or by any other property of the total situation. If this is the case, the nervous processes, in accordance with the law of deflection, must all be drawn into a single channel, the one leading to the motor response just referred to. That is, somewhere within the nervous system, they must all be united, as processes coming from Sa, Sb, and Sc, may be united in Sp. Now, the next moment, the same object may stimulate other sensory points, partly identical with or entirely different from the former. What enormously simplifies the whole problem is the fact that of all the
( 186) groups which might be stimulated by the same object, only those relatively few are ever likely to be stimulated which are displaced without any rotation, like the triangles in Figure 46. This new stimulation by the same object may result from either a movement of the object or a movement of the eyes or of the whole body. The objects which move are usually animals, moving over the ground without rotating around any horizontal axis within their body. Accordingly, their images on our retina do not suffer any rotation. If it is our body that moves, it does not rotate either, nor do our eyes, so that the image is again displaced on the sensitive surface without any rotation to speak of. The flux from the sensory points now stimulated is by deflection carried into the same motor point. Thus a large number of conductor groups of low resistance leading to the same motor point must be established all these groups having in common that the sensory points form a geometrical design of the same position with respect to the vertical; for other positions could be brought about only by rotation around a horizontal axis, which is a relatively infrequent occurrence in nature. Such a response having once been established—or else being inherited—it can be varied like any simple response by further experience. For example, the first response of a child to the sight of a cat may be one of shrinking; later, by variation, it may be one of approaching and petting the animal.
This is simple enough. The only question which might still be asked in order to make this kind of reaction to spatial stimulation—perfectly plain, is this: Why does the main flux, in case Sb and Sc, (in Figure 47) are stimulated together with equal intensity, pass in the direction of Sy? Why does it not pass in the direction of Spas well? Secondly, why does it not scatter almost equally in the directions of Sx, Sy, and SZ? To answer this question
(187) we need only refer to the law that nervous processes mutually attract each other. If one of them is stronger than the other, the result is a deflection of the weaker one from its course. If they are equally strong, the result is a union whenever the conditions of the case make a union of the several processes possible. Thus the two processes coming from Sb and Sc, instead of scattering in the directions of Sx, Sy, and Sz, unite in the only neuron in which they can unite most directly, the one leading to Sy, whence the flux goes on directly or indirectly toward the motor periphery. Saying that the flux takes its path over Sy, we mean, as always, strictly only that the major part takes this path and the muscular reaction depending on Sy overpowers all other muscular reaction. If Sa, is stimulated together with Sb and Sc, the three processes can not unite either in Sxor in Sy, but only in Sp. Accordingly, the muscular reaction is determined by Sp. That in consequence either of inheritance or of experience definite motor responses succeed group stimulations of a particular geometrical design, is thus made plain on the basis of our general assumptions.
Another one among the peculiarities of the so-to-speak sensory aspect of nervous function, of much interest to the psychologist because of its significance for the theory of esthetics, is the perception of melody and harmony in music. Certain tones, affecting the car either in succession or in simultaneity, bring about motor reactions like those which generally, in any division of sense, are the effect of stimulations of similar kind—similar in a greater or lesser degree. Neglecting the fact that these reactions to music are chiefly emotional to the question what emotional means `we shall return later we may use here the following quite possible and very concrete example. That the example is not taken from every one's daily
(188) experience may be excused by the fact that common behavior hardly ever contains any unemotional reaction upon musical tones. Suppose somebody has been trained to perform a particular responsive act whenever he hears the same tone twice with a short time interval between. The responsive act may consist in his saying simply "same tone" or "the tones are alike." We notice that he responds in this particular way frequently even when the second tone is an octave of the first, and also, though less frequently, when the second tone is a fifth of the first. Obviously, then, the nervous flux of the octave is, not identical with, but similar to that of the first tone stimulation; and the nervous flux of the fifth is also similar, though in a lesser degree, to that of the first tone stimulation.
If the first tone had been one of, say, four hundred vibrations and the second tone one of four hundred and five, it would not appear strange that the second nervous excitation should have affected the nervous system like the first. On an earlier page we spoke of the specific resistance of neurons. It goes without saying that any neuron having a specific resistance for the flux which is caused by the auditory sensory points being jerked four hundred times in a second, has this specific resistance also for a flux caused by slightly more, or less, frequently occurring jerks. But here observation teaches us that one neuron must apply the same specific resistance to a flux caused by jerks occurring in the ear twice ("octave") or one and a half times ("fifth") as frequently, —only in various degrees with various ratios. Rejecting all speculation on this point, we are compelled to accept the bare fact that with respect to the specific resistance of a neuron a simple ratio of jerks can take the place of a near number of jerks in the auditory organ. A full know-
(189) -ledge of the chemistry of the nervous flux may in the future make the evident fact plain to our understanding.
It does not follow, however, that in every neuron without exception a simple ratio must have this effect. On the contrary, there is good reason to believe that only a minority of all the neurons connected with the ear function thus, for there are even people—those who are entirely unmusical in whom practically no "ratio" reactions of this kind are found, who, we may assume, possess no neurons whatsoever of this vicarious function. In infancy, too, this function in auditory excitation seems to appear later than the other, so that we may regard it as a comparatively recent acquisition of the race. Now, if all the neurons do not apply their specific resistances to simple-ratio stimulation of the ear equally as to near-number stimulation, the subject's ultimate motor response, the muscular reaction proper, need not be identical in every case of similar and of simple-ratio stimulation of the auditory organ. An example will show what conditions are favorable to a response of this sort,—the nature of the just preceding reaction especially. Let a tone and its octave stimulate a person's auditory organ. Suppose that, a fraction of a minute before, many of those neurons have carried excitations which do not apply their specific excitations to simple-ratio stimulations of the ear:—two slightly mistuned tones may just have affected the ear. Then these neurons owing to their recent functioning, rather than the others, will function now again and the motor reaction to the two tones must be the usual one to two "tones quite different," because of their difference in the number of jerks. Our general explanation of that property of the nervous system which is the basis of all music (of melody and harmony) by no means involves us—as one might fear—in the difficulty that the motor reaction to tones of a simple
(190) ratio of vibration rate must inevitably be always the same as the motor reaction to tones of similar vibration rate.
No attempt will be made here to answer the question as to the origin of the fact that a limited number of the neurons of the human nervous system apply their specific resistance in various degrees to a variety of auditory nervous processes provided that the frequencies of the jerks received by the ear form certain simple ratios. Too much printer's ink has already been wasted on proposed answers to this question, of which none appears thus far entirely plausible.
A third peculiarity of the sensory aspect of nervous function, which we shall discuss here, is the rhythm which is often observable—not in animals but in man—in the motor reactions when the stimuli occur at fairly regular intervals but without being combined into any groups by physical accentuation, objectively. We mean by rhythm the subjective grouping, the fact that a definite, unitary response corresponds, not simply to each single stimulus, but rather to a group of stimuli, this group recurring in the sensori-motor activity with regularity for some time.
Take this example. I am sitting at the open window through which the regularly recurring puffs of a distant steam engine reach my ear. Suddenly I am imagining the strains of a waltz. The puffs of the engine seem to turn into the successive chords of the music and, at the same time, seem to have lost their former absolute regularity. They incite me to beat with my hand; but the movements of the hand are not all equal. Six of them fall into a group, and this group again consists of two parts of three beats each. The first of the six beats is executed with great vigor and mainly from the shoulder joint. The following two are executed with a much weaker movement
( 191) of the hand, and then too, the upper arm takes hardly any part in the motion, which occurs from the elbow joint rather, or even merely from the wrist. Vie total time occupied by these two beats is slightly less than double the time of the first beat. The fourth beat (the first of the second part is comparable to the first of the group, but has the same properties in a slightly lesser degree. The fifth and sixth are comparable to the second and third. We call this the perception of rhythm—of a particular rhythm in this particular case. How do I come to be affected in this peculiar way by absolutely regular puffs of a steam engine?
This habit of reacting is acquired by each individual in innumerable different ways. Let us at once give a concrete example. Imagine a gardener having planted a double row of plants like the stars of Figure 49. In order to keep

the loose earth, just thrown around the roots of each plant, from drying, it is necessary to compress it and thus render effective the capillary attraction which draws the moisture from the lower soil. The quickest way of doing the work is to walk along the center line of the double row and to step, with the full weight of the body, on each of the places which need compression, using, of course, alternately the right and the left foot. Now, try to walk ahead, doing this, and observe how your legs most naturally act during this procedure. While you are standing on your right foot, the muscles of your right leg are strained in such a way as to keep the leg straight and able to support the weight of the body, but not in such a
( 192) way as to throw readily the weight of the body upon the other foot. For this a complete readjustment of the muscles of the right leg is requisite. To bring about the muscular readjustment, you most naturally let the body fall lightly upon the left foot and let it swing back to the right. Thus you assume that new position on the right foot in which the tension of the various muscles is adjusted so that the full weight of the body can be thrown on the left foot forcefully and skillfully. The left foot now hits exactly the spot in the left row on the ground where the compression of the soil is needed.
What, then have you really done instead of stepping simply from the right foot upon the left? You have made two intermediate steps of a much less forceful kind, merely preparatory to the proper stepping on the loose soil. Before you now step on the next spot in the right row, you make again two preparatory steps, and so you continue your agricultural work most easily (that is, most naturally) and most effectively. Between each two compressing movements there are always two different preparatory movements, both of an easy character. Why just two different preparatory movements? Obviously because man is a symmetrically built and two-legged animal. If man were built like a horse, the total muscular activity might, and probably would, be rather different. Surely, if man were a three-cornered animal, the case would be entirely different,—most probably he would not even have any tendency then to plant his garden in double rows.
One must not think that all this cannot have much significance for rhythm, since most people who have rhythm have never planted any garden in the way indicated. This is true. The one example of human activity was only to show that the activities of man in general tend to be habitually of such a nature that the main motion is preceded
( 193) by a double or single (example below) preparatory movement of a less forceful kind. Thus the human nervous system becomes accustomed to muscular innervations arranging themselves in a group of three (or two) successive innervations of which one is strong. The individual possessor of the nervous system then has the habit of performing group activities rather than entirely uniform motions which follow each other like the puffs of an engine. He may then be said to have the habit of rhythmical perception, that is, the habit of reacting by a group activity to a series of perfectly uniform stimulations like our series of puffs, which directly, by their objective properties, in no way incite any group activity. That animals do not acquire any such habit of rhythm is readily understood if we only consider that horses or dogs do not habitually perform any systematic labor at all comparable to that mentioned above of a gardener. But in man's life systematic labor plays an important part—and not only labor, but also systematic play, like dancing a waltz. When the nervous system has once thoroughly acquired the habit of a particular group activity, this activity may by a "variation of response" quite readily show itself in a part of the body where it was not, and in a motion in which it was not, acquired, as when I beat with my hand the rhythm of a waltz while my feet, are at rest. It may by a further variation of response result in my naming an auditory impression as when, in reply to a certain question, I speak or write: "This is a waltz," without having in the least had recourse to counting up to three, the distinguishing number of that rhythm.
Our example of the gardener illustrated the acquisition of the habit, of triplet activity. We have also referred to the existence of the habit of doublet activity. If we are permitted to take our example again from agricultural
( 194) work—it is still easier to find examples in the shop or factory—we may imagine a gardener who has planted a single line of plants and has now to compress the soil at the successive spots. Suppose he does this with his left foot. He must then make before each compressing movement of the left leg one preparatory movement of the right leg (or three if he chooses, one of the right, one of the left, and one again of the right leg) in order to assume the proper position to the right of each plant. We thus have one weaker muscular innervation between each two of the main innervations, a group activity composed of two motions, one strong, one weak.
Our most common rhythmical perceptions are of the doublet and triplet kind. There are also familiar rhythms composed of four, six, eight, twelve, and sixteen units. These are simply compounds of doublets and triplets. For example, a group of twelve is a doublet of six, and this group of six again is a doublet of three; or the group of twelve may be a triplet of four, etc. We are very familiar with such groups in dancing. It is a common, but on that account no more correct, belief that people dance because of an inherited "sense of rhythm, "a special instinct which impels them to perform group movements of two, three, four, six, eight, etc., elements. The truth seems to be rather that we have a sense of rhythm because we dance than the reverse, that we dance because of an instinct of rhythm. Dancing is a group activity of our muscles which is easily learned because of its relative simplicity and its adaptation to the human anatomy. Since this activity is so easily learned and performed, it is used for sport, for play. Thus it becomes one of the sources of the general habits of rhythm.
All common rhythms are reducible to doublets and trip-
( 195) -lets by division with two or three. There is nothing mysterious in the fact that groups of five, seven, or nine units are not common rhythms. This is merely the consequence of the fact that systematic labor or play does not readily employ the human body with its two hands and two feet in such a way as to lead to the acquisition of a habit of combining, say, four different weak, preparatory motions with a strong, fifth motion into a single group. If one invents a certain playful activity of five or seven elementary motions—one of them being strong, the rest serving as different preparatory movements—and exercises it until it becomes perfectly habitual, he acquires a rhythmical perception of a quintuplet or of a septuplet which appears no less natural and quasi-inborn than the rhythmical perceptions of a triplet and doublet. Such has been the present writer's personal experience.
Let us understand, then, that the so-called "perception" as well as the execution of rhythm, as a nervous function, is simply successive group activity, involving in each case the successive innervation of a definite number of different muscle sets. One reason why in the textbooks rhythm is so shrouded in mystery is clearly this, that it is usually thought of as an instinctive nervous reaction to number instead of being regarded as a (numerical) habitual group of successive sensori-motor activities unified by their leading to a single end. Number enters into such a function really only as a conception of the scientist who describes it, not of him in whom the function occurs.