The Fundamental Laws of Human Behavior
FIFTH LECTURE
Max Meyer
Table of Contents | Next | Previous
Advantage of comparing the nervous process with a process of streaming. Analogy of the jet-pump. The whole nervous system permeated by any nervous process, but not with uniform intensity. Suction at motor points; openings made at sensory points. Velocity of the relief of tension. Conditions of the intensity of streaming at any definite point of the system. Exhaustion. Resistance increasing with, and even more rapidly than, the flux. Overflow not identical with universal permeation. The selective function of an instinct explained by the principle of deflection, the collective by that of overflow.
SPEAKING of the fundamental facts to which one customarily refers by the term instinct, we showed (page 53 and Figure 17) that one of them consists in the capturing of the nervous process going on in one reflex arch (Sd Md) by the nervous process going on in another reflex arch (Sa Ma), in such a manner that the former process, coming from Sd, could not reach its normal end in the motor point Md. Does it help us to understand this possibility of one nervous process capturing another, deflecting it from its normal coarse, if we compare nervous processes with the conducting mechanism of a pneumatic organ? It does indeed, although no such capturing takes place in an organ. The little bellows operating a pipe valve is filled by air streaming through the connecting tube. Now, it is one of the most interesting facts of
(60) physics that a stream can deflect another stream with which it is in contact. This is equally true for gaseous and liquid substances, there being in this respect no fundamental difference between them. We are all familiar with many kinds of apparatus using this principle of deflection. Think of the various sprayers for spraying perfumes or substances for inhalation, or for spraying with insecticides the vegetables growing in the fields. In these sprayers the liquid to be distributed is usually taken deflected, if we wish to say so—from the vessel in which it is contained, by a stream of air. Or think of the jet-pump, draining, perhaps, the cellar under our house, or exhausting air from a glass bell in our laboratory. It is not necessary for us here to discuss these phenomena from the standpoint of theoretical physics, to explain them mathematically. It is sufficient to mention them as familiar facts. In all these cases it is irrelevant, of course, whether the deflected stream really streams originally with a positive or a negative velocity or happens to have a zero velocity, that is, happens to stand still, as in most of the examples mentioned above. We can speak of deflection in every case.
Now, if the wandering of an excitation through a neuron is comparable to the streaming of a fluid, we understand at once the possibility of the deflection of one nervous process by another. This deflection of a nervous process from its ordinary course is then no longer a strange phenomenon, but has become like an old acquaintance. We no longer ask any curious questions about it. We might, possibly, inquire after the physiological details of this function of the contact point or points of the two nervous paths, where the deflection is brought about. But our curiosity in this respect is not very great as long as we do not even know the kind of chemical changes which are conducted through the neuron.
( 61)
We have spoken of a chain of neurons as if it were a tube through which air (or any fluid) is pressed from a reservoir containing air under higher pressure. There are, however, some disadvantages in picturing a nervous process in this way. There is actually nothing which resembles a reservoir from which any power or any substance enters, by way of a sensory point, into a chain of neurons in order to be pushed along; and this pushing by pressure might suggest a wrong idea of the function of the nervous system. Some one might think that, whatever it is that is pushed from a sensory to a motor point, it will take—like a rolling ball—only one way and entirely avoid all other possible ways. Thus, indeed, one finds nervous processes most commonly described in the older literature of neurology. The question would then have to be asked why such a process can take, now one, now another path, why it does not always take the same, since there is no god, no supernatural entity, in our nervous system to act as switchman, to sever the connections of the first path and to establish new paths, by voluntary action. This question is then unanswerable; the fact appears like a miracle. We must not think, therefore, of a nervous process as ever taking strictly a single path. We must, on the contrary, think of any nervous process as permeating the whole nervous system, but only along a certain path with great intensity, along all others with very small intensities. Only thus can we understand the function. of the nervous system as a unitary function. It is, therefore, better not to think of the nervous process as something being pushed, but rather as a fluid filling the whole network of neurons and being attracted by, sucked in the direction of, all the motor points of the body. It is true, to those who are accustomed to imagine in mathematical terms movements of a liquid or a gas, there is no
(62) essential difference between. a stream of a fluid caused by pressure at one end and a stream caused by suction at the other. But those not accustomed to mathematical reflections on such phenomena, will probably remember the all-permeating nature of any process in the nervous system more easily if they think of the cause of the streaming as something located in the totality of the motor points.
Let us, therefore, make the assumption, that the nervous system functions as if the neurons were tubes filled with a fluid, as if at all the motor points there were a constant suction tending to draw the fluid in the direction of each and every motor point, and as if an excitation of any sensory point were equivalent to a greater or smaller, but always minute, opening of the tube at this point, thus allowing a streaming motion of the fluid within the tube system. When a system of tubes like the diagram of Figure 16, with one-way valves at all the meeting points of tube-units, is closed at all those points which we have called sensory points, no streaming of the fluid is possible in any of the tubes, in spite of the suction at all the motor points. Another effect, however, results from the suction. The whole fluid in the tubes must assume a definite tension, whose force must become equal to that of the suction. Then the tension remains constant until a stimulus is applied to a sensory point, or, as we have said, until one of the tubes is slightly opened at a sensory point. One must not think that immediately when the opening occurs, the whole column of fluid begins to stream. What happens first, is a relief of the tension at the point where the opening is made. Then, as in every elastic substance, so in the fluid, the relief of tension passes on. Only when the relief of tension has reached the point where the force of suction is effective, that is, the motor point, can the
( 63) actual streaming begin. The velocity with which the relief of tension travels through the fluid, is exactly what is ordinarily called the velocity of sound in an elastic substance. In a neuron we have to call it the velocity of the nervous process,—whatever the nature of that process may be. The velocity of the nervous process, which may be regarded as a constant numerical value, and the length of the conductor leading from the sensory to the motor point determine, therefore, the time which elapses between sensory excitation and the start of the motor response.
The relief of tension, and the subsequent streaming, in a system like Figure 16, can take simultaneously many paths in the direction of a motor outlet. Which of all these paths is chiefly taken, is determined by the relative resistance of the conductors. We must not imagine,—as we have emphasized before and restate here in more detail that the relief of tension rolls on like a ball, striking an obstacle, rebounding, running into an open channel, and so on, finally reaching one motor point exclusively. The relief of tension travels to every motor point which is directly or ever so indirectly connected with the sensory point in question. That it reaches motor points of direct connection sooner than those of indirect connection, is clear; but this time difference does not especially concern us at present. The streaming, subsequent to the relief of tension, also occurs everywhere,—in every neuron which is a chain in any path from the sensory point to any motor point. But the intensity of the streaming, the flux at any definite point within the nervous system, is necessarily determined by the relative resistance of the total path over this point (not the resistance of any single point) from the sensory to the motor point and the resistances of all the other paths leading from the same sensory point to all the motor points. To get a more definite
(64) image of such a complicated phenomenon, let us think of two incandescent electric lamps illuminating our room, which in the ordinary manner are placed parallel into the circuit. Suppose the wiring provides for two twenty candle-power lamps, but we suddenly replace one of them by a 200 candle-power lamp of correspondingly less resistance. Immediately we see a diminution of the brightness of the other lamp, because its higher resistance keeps the current from passing through it in its normal strength. Now imagine that in Figure 18, which is
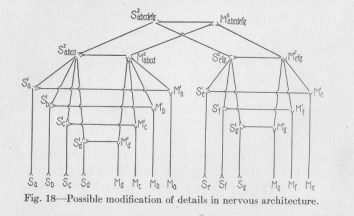
merely a modification of Figure 16 on the same structural principles, each neuron would be replaced by a thirty volt lamp and that then the point Sa would be placed in contact with the positive line, and all the M points in contact with the negative line of a hundred and ten volt electric circuit. It is clear that the three lamps of the reflex arch Sa Ma, would then glow visibly, but that the other lamps of the system would hardly glow at all, although a weak current must pass through them. Simi-
( 65) -larly, the muscular activity in the animal body becomes conspicuous only in the corresponding motor point, although a weak streaming must occur in the direction of every motor point in any way connected with the sensory point where the excitation starts.
If we thus picture the nervous process as a streaming of a fluid in a system of tubes, made possible by an opening at one of the sensory points, we must, of course, imagine this opening to be, even when at a maximum, very small relative to the volume of a tube unit. Otherwise the tube, or even the whole system, would quickly become empty, exhausted. The nervous system, however, is by no means quickly exhausted, but can be active for many hours before taking a complete, or nearly complete, rest (luring the period of sleep. The opening at a sensory point being exceedingly small, the streaming of the fluid must be very weak. This does not matter, since the flux in various neurons is significant only through. its relative, not its absolute magnitude.
Two fundamental facts, with reference to the so-called instinctive activities of animal organisms, were to be explained: the deflection of one nervous process by another, and the simultaneous enhancement of the activity of several motor points. We have found that the former becomes comprehensible if we regard any nervous process as possessing the properties of a streaming fluid, provided the meeting points of the neurons, about whose functional properties we possess no actual knowledge whatsoever, are assumed to function in a manner comparable to the functioning of the simple mechanical device which is called a "jet pump." The simultaneous enhancement of the activity of several motor points can be satisfactorily explained as we have explained it in the preceding lecture, simply by an overflow and the inherited peculiarity of
( 66) nervous connections. If the excitation starting from Sa in Figure 17 is not in the ordinary way practically confined to the reflex arch Sa Ma, but exceeds the capacity of the reflex arch and overflows, it will reach on a higher level the connecting neuron Sa2b3c3 Ma2b3c3 and hence pass down over the central point M2bc to both the motor points Mb(and also Mb)and Mc. Since the overflow finds an outlet from the level of 8¢2b3,3 down, it does not reach the higher level of Sa"b4e4d'. This is important, for, if the overflow from S¢ reached this level, the excitation starting from S¢would enhance the activity of the motor points Md and Md , instead of decreasing it by deflection, in accordance with our previous assumption concerning the significance of Mb, Mc, and Md in the instinct under discussion. The deflection of the nervous process SdMd, however, can be insured by a sufficient difference in level between the connecting neurons which in Figure 17 are represented by Sa2b3c3 Ma2b3c3 and by Sa3b4c4d4 Ma3b4c4d4 . This difference in level, of course, is not limited to what it appears to be in the simplified diagram of Figure 17. Only one question is thus left, namely, how we can speak of an overflow of a reflex arch (SaMa) upwards, caused by the intensity of the excitation (at Sa), with the result that the activity of certain other motor points (Mb and Mc) is not, as would be expected from the principle of deflection, weakened by the strong nervous process (from Sa), but on the contrary enhanced. This is a question of so much importance that we cannot proceed without having answered it with perfect clearness. It is particularly important to make clear the difference between an overflow and the fact that in the case of every nervous process very weak currents always go over innumerable paths other than the main path of the process.
It is obviously not sufficient to state simply that the stronger nervous process deflects all weaker ones. There
( 67) are exceptions to this rule, as in the present case. Every case in which, because of a very great excitation at a sensory point, the motor response is not practically restricted to the corresponding motor point, but becomes positively apparent also at other motor points, is an exception to the principle of deflection. The stronger process, instead of canceling the motor effects at all motor points other than its own, while it may cancel many of them, enhances at least some of them, indeed may bring about some motor effects at points whose corresponding sensory points are not receiving any stimulation at all. Now, this can be understood only by assuming that there is an absolute limit to the flux in any neuron, or,—what amounts practically to the same and agrees better with our previous assumptions,—that the resistance of any neuron is not independent of the flux within it, but increases more and more rapidly as the flux increases. We are familiar with a similar phenomenon in electric conductivity. As the current increases, the conductor gets hot; and in the case of most substances its resistance becomes the greater, the greater the temperature. Let us imagine that there is a similar, only much more rapid, increase of the resistance with the increase of the flux in a conductor, and our problem is solved. If, under this condition, the excitation at Sa in Figure 17 reaches a sufficiently great height, the intensity of the flux in the motor neuron M1a Ma reaches practically an absolute maximum, and the overflow, which thus becomes inevitable, must seek the motor outlet which offers the least resistance because of the least length. This is in the present case the outlet over Sa2b3c3 Ma2b3c3 M2bc into Mb,M’b and Mc. Of course, there can be, then, no question of any deflection of an independent nervous process in Sb,Mb or Sc Mc. Whether there is any such nervous
(68) process or not, the overflow from Sa into Mb and M, would occur anyway. At the same time, however, the nervous process SdMd, if Sd happens to be simultaneously stimulated, is deflected into Mb and Mc , provided the overflow from Sa has not reached the level of Sa3b4c4d4 Ma3b4c4d4 .
Overflow and deflection, therefore, are not fundamental principles which logically exclude each other. Their conditions merely enter now and then into a conflict, a state of affairs which is found in all natural laws. Let us keep in mind, then, that we do not mean by overflow—as someone might conclude who has not read our present discussion carefully—the fact that any nervous process permeates, although for the most part exceedingly weakly, the whole nervous system, far beyond the limits of a narrow path: we mean an overflow caused exclusively by an intensity of flux taxing the capacity of a nervous path to its limit.
We have called an instinct a selective and collective agency in the functioning of the nervous system. It is clear that the principle of deflection explains the selective, the principle of overflow the collective part of the function of an instinct, provided the inherited connections of sensory and motor points are such as represented diagrammatically in Figure 17.