The Fundamental Laws of Human Behavior
THIRD LECTURE
Max Meyer
Table of Contents | Next | Previous
Locomotion of the jelly-fish. Concerted action of all the divisions of the body and local responsiveness. Need of a gradation of connections differing in resistance. Corresponding points. Resistance dependent on length of conductors. Connections of non-corresponding points. Impossible manner of connecting the neuron arches. First improvement of manner of connection: One-way valves at the meeting points of neurons. Second improvement. The connections between the arches being themselves arches consisting of three neurons each.
WE have stated that the fundamental principle upon which the design, the architecture, so to speak, of the nervous system is based, is the following one. Each sensory point of the body is connected by a conducting string with a definite motor point of the body. The selection of a suitable motor point for connection is nature's proper business to which she has attended during a long process of evolution of the animal race. Every animal is born with fully developed connections of this kind, or, at least, with rudiments which by heredity are predetermined to grow into such connections during the individual's early life. If an animal is born without them, life is impossible.
However, it is easily seen that a nervous system of this extremely simple kind will need improvement as soon as
( 31) the animal race which possesses it makes progress from the most primitive to a somewhat higher organization of its bodily functions. Let us consider an example. A jelly-fish of the kind called acalepha still has an exceedingly low organization; yet it will make clear what we wish to understand. For locomotion it has a bell-shaped body, so that, on contraction of the bell, the whole body moves through the water in the direction of the closed end of the bell. When seen from the front the bell looks like Figure 10. On the periphery of the bell there are
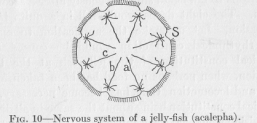
eight points (one of which in the figure is marked S). From each of these points conducting fibers similar to the fully developed neurons in higher animals pass into the neighboring tissues, but not far enough to come into actual contact with the fibers radiating from any other point S. The purpose of these fibers is clear; they conduct any excitation occurring at any point of the rim with but slightly diminished effectiveness to all the tissues of that eighth-division, causing thus a uniform response of the whole division to any stimulus applied to any one of its points. In addition to these one fiber seems to pass from each S in the direction of the center of the bell. For what purpose? Obviously, to make it more certain that during the process of locomotion no division of the bell lags behind the others in contraction.
( 32) It is plain enough that no straight-way locomotion would result if, for example, the tissues on one side of the rim would contract when, having lagged behind, all the diametrically opposite tissues are still in expansion. This lagging behind, however, would frequently occur. To understand it readily, let us imagine the analogous case of eight leaky places on a water pipe. Suppose the frequency of the dropping at each place to be about the same, say, one drop a second. But even then we could not expect all the drops to fall simultaneously, eight further drops to fall again simultaneously after a second, and so on. The eight drops would fall in a quite irregular succession. Let us make the application to our case. The rhythmical contraction would be caused by the chemical constitution of the jelly-fish at the time in question, when perhaps no food has been taken for some time and locomotion thus has become necessary. The chemical constitution being about the sane in all divisions, no division would have a frequency of periodic contraction differing much from that of any other division of the body. Nevertheless, the contractions would not occur in the eight divisions simultaneously any more than the falling of the eight drops spoken of -above. But this simultaneity could be easily insured by connecting the eight divisions by conductors. Now, as soon as one of the divisions spontaneously begins to contract, this contraction causes an excitation in the nervous plexus of that division. This excitation is carried to all other divisions and at once all other divisions begin to contract.
This connection of all the divisions of the body would work beautifully if no other kind of locomotion were ever needed than straight-way locomotion in response to an internal stimulus, the chemical constitution of the body at the particular time, for example, some time after the
( 33) last taking of food. But frequently external stimuli act upon the body and require, not a straightforward locomotion, but a change of direction as response. For example, the jelly-fish, while swimming, strikes a rock with one side of the bell. The jelly-fish then must change its direction. That division which touched the rock must contract more strongly than any other, especially than the diametrically opposite division, in order to bring about the change of direction. Without conduction, the predominance of the action of the one division touched would be certain. But with perfect conduction to all other divisions it would be equally certain that no such predominance of a local reaction, no local responsiveness to an external stimulus would be possible. Here is, then, the necessity of a compromise. And this compromise is effected by having the eight radial fibers not join in. the center, but stop short before reaching each other. Thus undifferentiated tissues, tissues of high resistance, are interposed to weaken the excitation coming from one of the divisions to such an extent that only one division can react strongly to the external stimulus. All others react only weakly.
One must not think that for a concerted action of all divisions of the bell, like the action of straightforward locomotion, string-like conductors of differentiated tissue are indispensable. The various divisions of the rim of the bell might force each other into the same periodicity and, what is still more important for our present consideration, into the same phase of periodic contraction through the ordinary conductivity of the undifferentiated tissues. Whatever division is at any moment the first to contract, might send its excitation by means of conduction through the undifferentiated tissues to all the others and thus force the whole rim to contract at the same time. This
( 34) is the more possible when the periodic contraction of each particle is not the result of an. external stimulus but, as - we have seen, the result of a chemical constitution at any given time practically uniform throughout the whole body. The stimulus coming from one division, not having to cause, but only to hasten in all the others the contraction which would have occurred a little later anyway, need be only weak. Nevertheless, the question remains if it would not be too weak if it had to pass wholly through undifferentiated tissue. Nature, therefore, must make the radiating conductors just long enough to meet this condition of reducing the resistance just enough for concerted action; but not the least longer, for every increase of their length is equivalent to cutting down the local responsiveness without which the animal could not survive. We understand thus why the radiating fibers do not join in the center.
It is interesting to note that compromising, which is the very foundation of all social life of animals, of all social institutions of mankind, is found to be an essential function in the individual life of any one of the very lowest animals which possess a nervous system. The unity of all organized nature, which is the fundamental concept of modern biology, is exemplified by this role played in any life, low or high, by compromises. Two conflicting conditions seem to make life impossible. But the problem would be hopeless only if a complete denial of the demands of either the one or the other were insisted on. On the one hand, concerted action calls for the most perfect conduction from any division of the rim of the bell to all the others. On the other hand, local responsiveness calls for the interposition of high resistances between the diametrically opposite divisions of the rim. The compromise must then consist in this, that all the divisions are
( 35) connected by conductors, but in such a way that conduction from one point of the rim to opposite points is by the properties of the conducting medium itself more resisted than conduction to neighboring points. Nature has, as we saw, solved the problem by stopping the differentiated radiating conductors as far short of the center as the condition of local responsiveness requires, leaving in the center enough undifferentiated tissue interposed to meet this requirement. Another way of fulfilling the condition of varying resistance is by resorting to the length of the differentiated conductors without interposing any undifferentiated tissue. There can be no doubt that the length of a nervous conductor determines its resistance as the length of telegraph and telephone wires determines their resistances. The longer the conducting string, the greater its resistance. Nature has solved the problem in this way in another kind of jelly-fish, called hydromedusa. Here all the points of the rim are connected by differentiated conductors forming a ring, as shown in Figure 11.
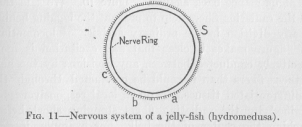
If any division of the rim contracts, the excitation is by this ring conducted to all other divisions. But the excitation reaching opposite divisions of the rim is much weaker than that which reaches neighboring ones, in accordance with the varying length of the conductor. This difference in the intensity of the conducted excitation does no harm
( 36) in the case of ordinary, straightforward locomotion. The rhythmical contraction is in this activity the result of the chemical constitution of the body which, perhaps, has been the result of lacking food for some time. This chemical state differs but slightly in the various parts of the body. The different divisions of the rim, therefore, would contract and expand in almost the same periodicity anyway. A very slight excitation conducted from elsewhere is then sufficient to hurry up any division which without this excitation would lag behind. But when a stimulus acts from without on any point of the rim, only those divisions are caused to respond strongly to the stimulus which are in the neighborhood of the stimulus. The other divisions of the rim, receiving a weaker and weaker excitation the longer the piece of the rim over which the excitation has to travel, are considerably affected only in the neighborhood of the point of stimulation. The divisions opposite this point remain practically unaffected by the stimulus.
Let us glance back again at Figure 10. We said that (1) the radiating fibers help to prevent the lagging behind of any division in the ordinary activity of locomotion. The figure makes it clear that any excitation is more effectively conducted between any divisions by the help of these fibers than it could be conducted through the undifferentiated tissues. (2) The local responsiveness is retained by the radiating fibers stopping short before reaching the center of the bell. For example, if S is stimulated by an external influence, the excitation is carried also to a, b, and c, but more weakly to a and b and very much more weakly still to c. In order to reach c the excitation has to pass from the radiating fiber S to the radiating fiber c over a rather long step of undifferentiated tissue. Undifferentiated tissue has a much higher
( 37) resistance than nervous tissue. Consequently, the excitation reaching the points, a, b, and c, is more and more weakened, and no interference with the local responsiveness at the point S can appear. If the radiating fibres did unite at the center of the bell, a, b, and c would all be equally excited. The problem of universal connection of all parts of the body by conductors of low resistance, combined with undisturbed local responsiveness, can therefore be solved architecturally in more than one way. Figures 10 and 11 represent two solutions of the problem, both found in nature. But the solution of Figure 11 is the more perfect one, because the universal communication through conductors is more perfect, while local responsiveness is as satisfactorily retained as in the other case.
The example of the jelly-fish has taught us that one kind of nervous connections within the animal body is not sufficient. There must be many kinds,-or rather, there must be a gradation of connections differing in the resistance offered by the conductor in the various cases. If it is desirable for an animal's well-being that an excitation occurring at a certain point, say A, be followed most readily by a contraction at the point a, the points A and a must be connected by a conductor of small resistance. Let us call those points which are thus connected corresponding points, in order to have a brief term by which we may refer to them. If, as in the case of a jelly-fish, these corresponding points A and a are practically identical, the conduction is a self-evident fact even without any special conductors. If, as in the case of the moth, A is an eye and a the muscles of a wing, the conduction between the corresponding points must be mediated by a nervous string, or chain of nervous strings, of the shortest length possible under the anatomical
( 38) conditions. But all---or at least some-of the other (non-corresponding) contractile points of the body must also be in sonic way connected with the point A. Otherwise, no concerted action would be possible. The jellyfish would, for example, be scarcely capable of swimming straight ahead; the moth would hardly be able to alight on a twig or leaf which happens to impress itself on the moth's eye and towards which the moth must act, not only with its wings, but also with its legs. These further connections with the point A, however, in order to leave the connection A-a in its proper functional order, must have a higher resistance,-as we have seen, must be longer than A-a.
In higher animals, whose tissues are all differentiated to perform special functions, the nervous connections are practically all connections between sensory and motor points, that is, between points of the body which are by differentiation specially sensitive to particular physical or chemical influences, and points which are of differentiated contractile tissue. It is true that nerve fibers are also found to end in tissues which are not contractile; in glands, for example. However, these cases are the minority, and may be left out of the discussion here, since we are especially and directly interested in behavior only, which depends, of course, on the function of contractile tissues, of muscles. We have represented in Figure 5 the short-or direct, as we may say-connections between corresponding sensory and motor points in the shape of arches. We must now find a way of representing graphically those nervous conductors which lead from each sensory point to those motor points which are not corresponding. These conductors must be, as we have found, longer than the conductors directly connecting corresponding points. It is clear, then, that we could not
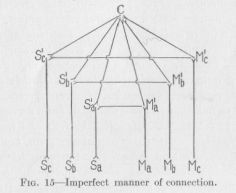
(39) represent the conductors connecting non-corresponding points as they are represented in Figure 12. This figure is shown here merely because some books, treating these problems somewhat superficially, actually give figures like this as an example of how nervous connections are constructed. Let us agree that any straight line which has no cross-connecting point between its ends, shall always represent a standard length, and also, unless anything is said expressly to the contrary, a unit of resistance Such lines as S1aM1b, which has a crook inserted between its straight ends, are included under this definition. This line is drawn so as to indicate that it is not in contact with S1bM1a; for this purpose the method of drawing which is generally used by electrical engineers to indicate crossed, but mutually insulated wiring, has been adopted. A glance at the Figure 12 shows that the conductor
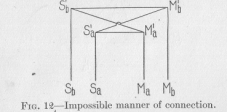
Sb S1bM1aMb connecting the non-corresponding points Sb and Ma has not a greater resistance than the conductor Sb S1bM1bMb, since both are made up of three standard lengths, although our requirement is that it shall have a greater resistance. We must look for a different kind of graphic representation to suit our needs.
Neurology, that is, the anatomy and physiology of the nervous system as it actually exists and functions in animals and in man, teaches us an important fact which we ought to represent in any diagram of nervous connec-
( 40) -tions. It has been found that the same two points (one sensory and one motor) arc almost generally connected in several ways, by shorter and also by longer conductors. For example, if pain is caused in a dog's foot and the foot is withdrawn, the nervous excitation may travel from the foot to the spinal cord and thence to the muscles moving the foot. Or, it may travel from the spinal cord farther on to the dog's brain, thence back to the spinal cord and now only to the muscles. If we combine this requirement of a two- (or many-) fold connection of greater and lesser length between corresponding points with our previous requirement that the connections of non-corresponding points shall be longer than the (direct) connections of corresponding points, the diagram of Figure 13 readily suggests itself. We draw four conducting
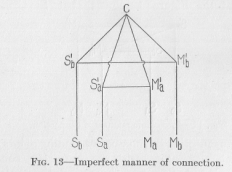
strings from S1a, S1b, M1a, and M1b and unite them in a central point which we may call C. All our requirements are then fulfilled. We can travel from Sa to the corresponding point Ma over a longer route by C (four standard lengths), or over a shorter route (three standard lengths) avoiding C; and we can travel from Sa to the non-corresponding point Mb only over a longer route
( 41) Sa S1aCM1bMb of four standard lengths. The same holds good for starting from the sensory point Sb.
Nevertheless, this diagram of Figure 13 is not, yet quite satisfactory, but must be perfected in at least two ways. First, an excitation starting from one sensory point, for example Sa, in Figure 13, cannot only pass, over various routes, as we have seen, into the conductors M1aMa and M1bMb , but also from C into the conductor CS1b and from M1b into the conductor M1bS1b, and then further from S1b into the conductor S1b Sb. Thus the excitation, whose ultimate end is naturally the causation of contraction in contractile tissues, would be only partly used for this end; a large part would be wasted by going into sensory points where, in animals with highly differentiated tissues, no contraction is possible. We must, therefore, draw our diagram in such a manner that the passing of any excitation into a sensory point is excluded. One way of doing this is by drawing each conductor, each neuron, in the shape of an arrow-like rod as shown in Figure 14. We
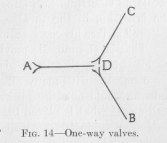
can then easily agree and remember that the point of any arrow shall mean that no excitation can enter here from any other neuron, whereas the split end shall mean that an excitation can enter here, but can not pass out. Any point like the point D in Figure 14, where several neurons
( 42) meet, indicates then, according to the manner of drawing, that an excitation may pass from AD into either DB or DC, but that no excitation can pass from either CD or BD into DA. It is as if a double one-way valve located at D allowed the flow of a fluid in one direction, but prevented the flow in the opposite direction. We must ask, of course, if the facts known to neurology permit the assumption that the meeting point of two or more neurons functions like a one-way valve.
Experiments have proved, it is true, that an excitation may travel to the other end of a neuron, in whatever end it is called into existence by the application of an artificial stimulus. But with respect to the propagation from neuron to neuron, neurological experiment and observation seem to agree with the view expressed in the diagram of Figure 14. Everybody knows that our feet are connected with our eyes as well as with our ears, and, of course, also with other sense organs. If a strange and ferocious looking animal suddenly appears to any ordinary person's eye while he is sitting, he jumps up and starts running. If he is sitting in the theater, and suddenly the fearful cry "fire" strikes his ear, he also jumps up and starts running. That is, the muscles moving his feet are connected with his eye as well as with his ear. But his eye and ear are connected with many other muscles too; else, for example, he would not turn his head in response to a friend's call or eat what is placed before him on the dinner table. Now, neurologists have discovered in the brain the so-called motor region of the foot. If this region of the brain is artificially stimulated, the muscles belonging to the foot contract and move the foot. Suppose the excitation caused by the stimulus could proceed, not only in the direction of the motor organs most closely connected, but also in the direction of sense organs, for
( 43) example, the eye and ear. The eye and the ear are very closely connected with the motor region of the foot in the brain; they are also very closely connected with many other muscles of the body. It should then have been observed that in response to the artificial stimulation mentioned not only the foot, but many parts of the body moved. If such were the case, the neurologists would never have discovered the motor region of the foot. This very discovery means that they observed an exclusive reaction of the foot to stimulation of this region of the brain. We are justified, then, in our assumption of a one-way propagation of an excitation from neuron to neuron. We need not assert, dogmatically, that no other interpretation of the experimental facts is possible. But the assumption of one-way conduction from neuron to neuron, always away from sensory points and toward motor points, is simple enough and does not contradict any known facts. Besides, the anatomical connection between neurons is of such a wonderfully elaborate kind, that it seems quite probable that the meeting points have a peculiar function, actually perhaps much more complicated than the simple function of a one-way valve. The neurons do not run into each other like wires soldered together, but their end branches are interwoven. The purpose of this method of connection is not known, but it surely involves more than a mere making one out of two.
We said above, with reference to Figure 13, that the diagram of that figure needs additional features in order to make it more perfect. First, then, we shall draw the meeting point of several neurons in the manner of Figure 14, indicating for each neuron the direction from a sensory point and the direction towards a motor point. A second improvement is necessary because the diagram of Figure
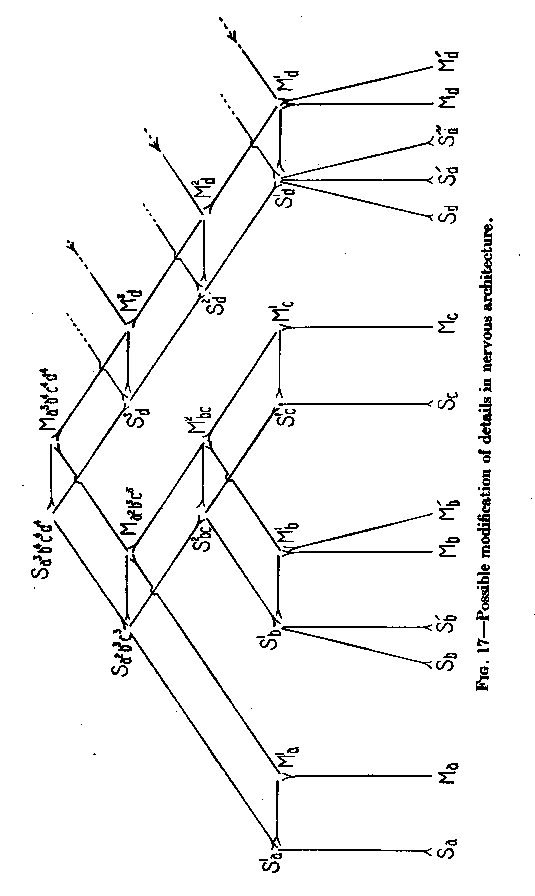
( 44) 13 does not permit the representation of a, series of motor points which can all be reached from one definite sensory point, but only over conductors each differing in resistance from all others. These conductors, in order to have each its special resistance, must all differ in length. At the same time, each motor point may have its own sensory point with which it is connected by a conductor of minimum length. The whole case, then, is somewhat comparable to that of the jelly-fish in Figure 11, where all contracting points can be reached from any point stimulated, but only over paths differing in resistance. The insufficiency of the diagram of Figure 13 becomes clear if we enlarge it by connecting (in Figure 15) in the same way not only two, but three pairs of corresponding points. In Figure 15 an excitation can travel from Sa, to Ma, over a path of three standard lengths. From Sa to Mb an excitation can travel only by C over a path of four standard lengths. We have, therefore, a difference of resistance. But from Sd to Mc, there is again a path of four lengths, so that there is no difference of resistance between the path leading to Mb and that leading to Mc. In order to represent a gradation of resistances we need a diagram differing from that of Figure 15. Instead of a point C, we have to introduce a line, as shown in the horizontal lines of Figure 16, representing each a neuron of standard length and resistance. In other words, the connections between the arches must themselves be arches consisting of three (or more) neurons each.
In Figure 16 three colors have been used in order to facilitate the recognition of the direction from sensory points to motor points. All green conductors in the figure can be traveled only in the direction from below up, all red ones only in the direction from above down, all violet ones only in the direction from the left to the right.
We can travel, in Figure 16, from Sa to Ma, over S1a and
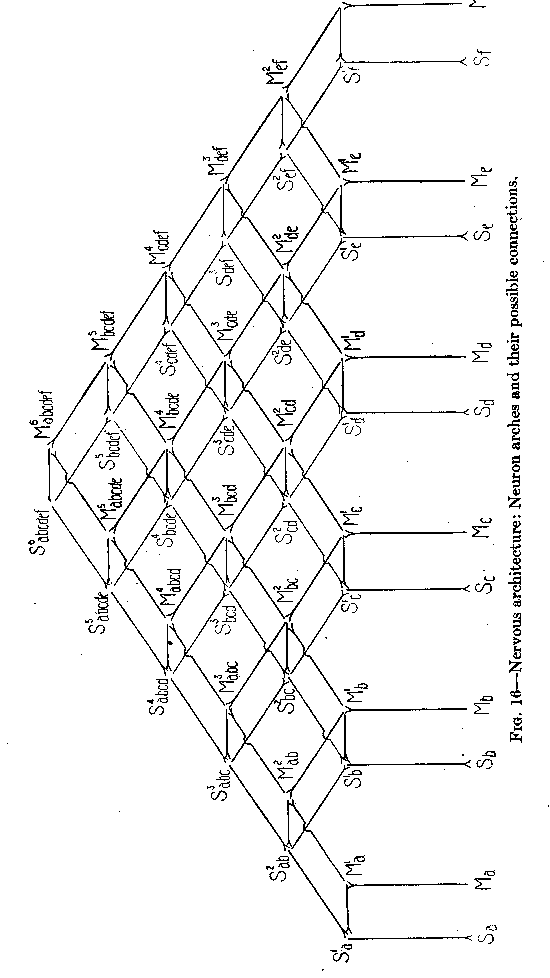
( 45)M1a, directly, taking a path of three lengths. From Sa to Mb the shortest path is over S1a, S2ab, M2ab, and M1b. This path has a total length of five units, two more than from Sa to Ma.
From Sa to Mc the shortest path is over S1a, S2ab, S3abc, M3abc, M2bc, M1c . This path has a total length of seven units. At the same time the corresponding points Sb and
Mb are connected by a short path (Sb, S1b, M1b, Mb) of three units, the corresponding points Sc and M, also by a short path (Sc, S1c, M1c, Mc) of three units. This diagram, therefore, exactly fulfils the condition of universal connection without interference with local responsiveness of an animal's body. We shall have to investigate whether a nervous system like the one represented in Figure 16 is sufficient for the needs of all the higher and the very highest animals,-whether we have a right to assume that even the nervous system of man is built essentially (apart from simplification and elaboration of the details) on the design of this figure. We have, of course, the right to assume this, if we can convince ourselves that all the actual functions of the nervous system in man's body are thus made comprehensible.